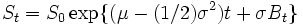幾何ブラウン運動
幾何ブラウン運動
幾何ブラウン運動
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/02/09 03:42 UTC 版)
以下の確率微分方程式、 d X t = μ X t d t + σ X t d B t {\displaystyle dX_{t}=\mu X_{t}\,dt+\sigma X_{t}\,dB_{t}} は重要な例であり、この解を幾何ブラウン運動(きかぶらうんうんどう、英:geometric Brownian motion)という。これは、数理ファイナンスにおいて、ブラック・ショールズ・オプション価格モデルで、株式価格の動きを模す方程式である。
※この「幾何ブラウン運動」の解説は、「確率微分方程式」の解説の一部です。
「幾何ブラウン運動」を含む「確率微分方程式」の記事については、「確率微分方程式」の概要を参照ください。
- 幾何ブラウン運動のページへのリンク
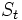 が
が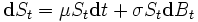
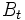 は
は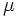 ,
,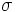 は,ある
は,ある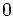 での
での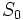 を
を