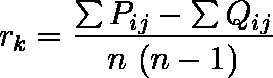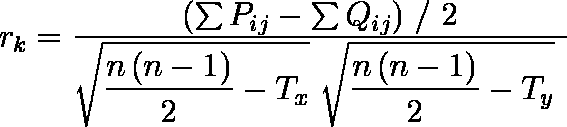ケンドールの順位相関係数とは何？わかりやすく解説 Weblio辞書

ケンドールの順位相関係数

例題：
　「表 1 において，変数 X と変数 Y の間のケンドールの順位相関係数を求めなさい。」

表 1．二変数データ
i	1	2	3	4	5	6	7	8	9	10
変数 Xi	2.8	3.4	3.6	5.8	7.0	9.5	10.2	12.3	13.2	13.4
変数 Yi	0.6	3.0	0.4	1.5	15.0	13.4	7.6	19.8	18.3	18.9

計算手順：

ケース数を n とする。
変数 X と変数 Y について小さい方から順位をつけ，変数 X について小さい順に並べ変える（同順位の場合には平均順位をつける）。
Yi（ i = 1， 2， ... ， n - 1 ）について，Yi ＜ Yj の個数を Pi ，Yi ＞ Yj の個数を Qi とする（ j = i + 1 ，i + 2， ... ，n ）。
例えば，表 2 に示すように，X5 に対する Y の順位は 7 であり，それより右にある Y の順位のうち，大きいものは Y8 ，Y9 ，Y10 の 3 個（ P5 = 3 ），小さいものは Y6 ，Y7 の 2 個（ Q5 = 2 ）。
Pi + Qi = n - i ，Σ ( Pi + Qi ) = n ( n - 1 ) / 2 となることに注意。
Σ Pi は 2 変数の順位の方向が一致する回数，Σ Qi は 2 変数の順位の方向が逆方向に一致する回数なので，Σ Pi - Σ Qi は順序の一致性の指標である。
- 2 変数の順序が完全に一致するときには，Σ Pi = n (n - 1) / 2，Σ Qi = 0 である。
- 2 変数の順序が逆順に完全に一致するときには，Σ Pi = 0，Σ Qi = n (n - 1) / 2 である。
このようなことから，次式を定義すれば， - 1 ≦ rk ≦ 1 となる。これがケンドールの順位相関係数である。

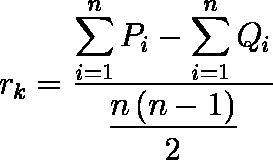
例題では，Σ Pi = 37，Σ Qi = 8 なので，rk = ( 37 - 8 ) / ( 10・9 / 2 ) = 0.64444 となる。
- 相関係数が正の場合「二変数には正の相関関係がある」という（正相関）
- 相関係数が負の場合「二変数には負の相関関係がある」という（負相関）
- 相関係数が０に近いとき「二変数は無相関である」という

表 2．ケンドールの順位相関係数の計算例
i	1	2	3	4	5	6	7	8	9	10
変数 Xi の順位	1	2	3	4	5	6	7	8	9	10
変数 Yi の順位	2	4	1	3	7	6	5	10	8	9
Pi	8	6	7	6	3	3	3	0	1		Σ Pi = 37
Qi	1	2	0	0	2	1	0	2	0		Σ Qi = 8
Pi+Qi	9	8	7	6	5	4	3	2	1		Σ ( Pi + Qi ) = 45

注：

どちらか一方（または両方）の変数において全てのケースが同一の値をとる場合には，相関係数は定義できない。
同順位がある場合には，変数 X，変数 Y における同順位の個数を nx ，ny ，同順位の大きさを ti ，tj（ i = 1，2， ... ，nx ；j = 1，2， ... ，ny ）としたとき，次式で計算される。同順位がない場合には Tx = Ty = 0 となり，前式に等しい。

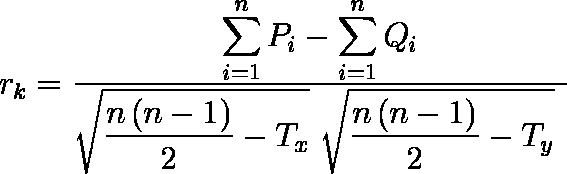
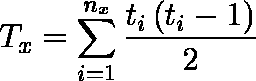
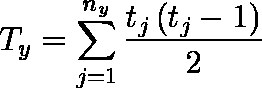
注意：上の定義では，変数 X と変数 Y のいずれかに（両方に）同順位があるかで取り扱いが曖昧になることがある。
そこで，ケンドールの順位相関係数のもう一つの定義法を示しておく（同順位がない場合は同じ結果が得られる。また，この方法では順位付けをする必要はない）。
変数の組 ( Xi ，Yi ）と ( Xj ，Yj ）を考える（ i ≠ j ）。
- Xi ＞ Xj かつ Yi ＞ Yj のとき Pij = 1
- Xi ＜ Xj かつ Yi ＜ Yj のとき Pij = 1
- Xi ＞ Xj かつ Yi ＜ Yj のとき Qij = 1
- Xi ＜ Xj かつ Yi ＞ Yj のとき Qij = 1
として，Σ Pij - Σ Qij を求める。
- 同順位がないとき
  　　
- 同順位があるとき
  　　
  　　Tx ， Ty は前述の通り。

ケンドールの順位相関係数

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/12/26 14:32 UTC 版)

この記事は英語版の対応するページを翻訳することにより充実させることができます。（2024年5月）

翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。

英語版記事を日本語へ機械翻訳したバージョン（Google翻訳）。
万が一翻訳の手がかりとして機械翻訳を用いた場合、翻訳者は必ず翻訳元原文を参照して機械翻訳の誤りを訂正し、正確な翻訳にしなければなりません。これが成されていない場合、記事は削除の方針G-3に基づき、削除される可能性があります。
信頼性が低いまたは低品質な文章を翻訳しないでください。もし可能ならば、文章を他言語版記事に示された文献で正しいかどうかを確認してください。
履歴継承を行うため、要約欄に翻訳元となった記事のページ名・版について記述する必要があります。記述方法については、Wikipedia:翻訳のガイドライン#要約欄への記入を参照ください。
翻訳後、{{翻訳告知|en|Kendall rank correlation coefficient|…}}をノートに追加することもできます。
Wikipedia:翻訳のガイドラインに、より詳細な翻訳の手順・指針についての説明があります。

ケンドールの順位相関係数（けんどーるのじゅんいそうかんけいすう、英: Kendall rank correlation coefficient）やケンドールのタウ係数（英: Kendall's Tau coefficient）は、順位（Ranking)間の相関計測に用いられ、相関の強さを表す。言い換えれば、それは複数のデータ間（cross tabulations）の関連性（association）の強さを表す。1938年にモーリス・ケンドール（Maurice Kendall）によって開発された。

順位相関を計測する別の方法としてはスピアマンの順位相関係数があるが、両者はほぼ同じ傾向を示す^[1]。

定義

順位データ x = (x₁, …, x_n) と y = (y₁, …, y_n) とのケンドールの順位相関係数 τ は次で定義される^[2]。

{\begin{aligned}\tau &={\frac {K-L}{\binom {n}{2}}}\\K&=\#\left\{\,\{i,j\}\in {\binom {[n]}{2}}\mid x_{i}\lessgtr x_{j},\ y_{i}\lessgtr y_{j}\,\right\}\\L&=\#\left\{\,\{i,j\}\in {\binom {[n]}{2}}\mid \neg (x_{i}\lessgtr x_{j},\ y_{i}\lessgtr y_{j})\,\right\}\end{aligned}}

カテゴリ

ケンドールの順位相関係数とは？わかりやすく解説