ベイズ‐すいてい【ベイズ推定】
ベイズ推定
【英】：Bayes estimation
パラメータ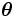
そのものやパラメータの関数(信頼度, 平均故障時間間隔など) 
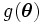を推定する場合に, 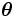の事後分布が有する情報を用いて推定を行うことを意味する. なお, 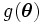の事後分布(事前分布を用いることもある)に関する期待値をベイズ推定量と呼ぶ.
| 信頼性・保全性： | フォールトトレランス ベイズ信頼性 ベイズ信頼性実証試験 ベイズ推定 ベイズ統計 保全性 信頼度 |
ベイズ推定
ベイズ推定
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/10/24 08:48 UTC 版)
詳細は「ベイズ推定」を参照 ベイズ推定は、推定における不確かさが確率を使って定量化される統計的推定を指す。古典的な頻度主義的推定（英語版）では、モデルのパラメータと仮説は固定と見なされる。確率は頻度主義的推定においてはパラメータまたは仮説に割り当てられない。例えば、頻度主義的推定においては、公正な硬貨を次に投げた時の結果といった一度しか起こりえない事象へ直接的に確率を割り当てることは意味をなさない。しかしながら、表が出る割合が硬貨投げの回数が増加するにつれて2分の1に近付くと述べることは意味をなす。 統計モデルは、いかに標本データが生成されるかを表わす一連の統計的仮定および過程を規定する。統計モデルは修正可能な数多くのパラメータを持つ。例えば、硬貨はベルヌーイ分布からの標本として表わすことができ、これは2つの可能な結果をモデル化している。ベルヌーイ分布は一方の結果の確率に等しい単一のパラメータを有し、ほとんどの場合これは表が着地する確率である。データに対するよいモデルを考案することがベイズ推計において中心となる。ほとんどの場合において、モデルは真の過程を近似するだけであり、データに影響する特定の因子を考慮に入れない。ベイズ推計において、確率はモデルのパラメータに割り当てることがでできる。パラメータは確率変数として表わすことができる。ベイズ推計はより多くの証拠が得られたまたは知られた後に確率を更新するためにベイズの定理を用いる。
※この「ベイズ推定」の解説は、「ベイズ統計学」の解説の一部です。
「ベイズ推定」を含む「ベイズ統計学」の記事については、「ベイズ統計学」の概要を参照ください。
ベイズ推定
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/06/26 07:13 UTC 版)
詳細は「ベイズ推定」を参照 ベイズの定理と組み合わせて確率的推論を行う方法がラプラスによって始められ、現在言うところのベイズ統計学の端緒となった。事象の確率という考え方を採用する特徴がある。 現在は例えば、迷惑メールの発見・分類といった作業のコンピュータを用いた自動化（フィルタリング）等のふるい分けにも利用されている。
※この「ベイズ推定」の解説は、「ベイズの定理」の解説の一部です。
「ベイズ推定」を含む「ベイズの定理」の記事については、「ベイズの定理」の概要を参照ください。
ベイズ推定
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/05/17 07:00 UTC 版)
詳細は「ベイズ推定」を参照 ベイズの定理を用いて、新しい証拠に照らして命題 θ i {\displaystyle \theta _{i}} の尤もらしさ（確率）の値 p i {\displaystyle p_{i}} を改訂していく方法がベイズ推定である。改訂前の値を事前確率、改訂後を事後確率と呼ぶ。事後確率は最良な推定結果そのものとなる。 例えばラプラスはこの方法で土星の質量を見積もった（土星の質量の推定値の事後確率分布 p ( m sat ) {\displaystyle p(m_{\text{sat}})} の期待値 m ¯ sat {\displaystyle {\bar {m}}_{\text{sat}}} を計算した）。 しかし頻度主義による確率の定義では、このような適用はできない。土星質量の推定値は確率変数ではないからである。「土星の質量とはどんな母集団から抽出されたものか?」という問いに答えられなければ、これは頻度主義者の議論の対象にはならない。
※この「ベイズ推定」の解説は、「ベイズ確率」の解説の一部です。
「ベイズ推定」を含む「ベイズ確率」の記事については、「ベイズ確率」の概要を参照ください。
- ベイズ推定のページへのリンク
