ベイズの定理
ベイズの定理
2 つの事象 A,B があるとき,
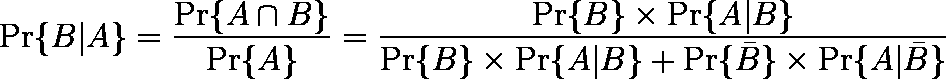
を ベイズの定理 という。
一般的には,B が r 個の排反事象に分かれるとき,観察された事象 A の原因が Bi である確率は,
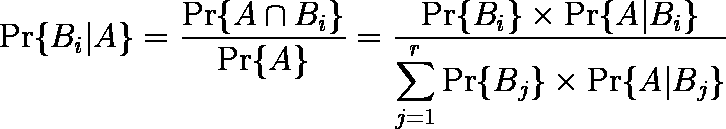
となる。Pr{Bi} は 事前確率,Pr{Bi | A} は 事後確率 と呼ばれる。
例えば,A が女性であること,Bi が学年( i = 1,2,3,4 )としたとき,Pr{Bi | A} は,ランダムに抽出した学生が女子学生であるとわかったとき,その学生が Bi 学年である確率を表す。
| 学年 | 男子 | 女子 | 合計 | 女子の割合 | 学年の割合 | ベイズ確率 | |
|---|---|---|---|---|---|---|---|
| Pr{A | Bi} | Pr{Bi∩A} | Pr{Bi} | Pr{Bi | A} | ||||
| B1 | 90 | 36 | 126 | 36/126 | 36/510 | 126/510 | 0.2209 |
| B2 | 76 | 45 | 121 | 45/121 | 45/510 | 121/510 | 0.2761 |
| B3 | 87 | 43 | 130 | 43/130 | 43/510 | 130/510 | 0.2638 |
| B4 | 94 | 39 | 133 | 39/133 | 39/510 | 133/510 | 0.2393 |
| 合計 | 347 | 163 | 510 | Pr{A}=163/510 | |||
事前にわかっている確率は Pr{Bi}, Pr{A | Bi} だけでよい。
事後にわかった事実 “女子である” ということから,事後確率 Pr{Bi | A} を得ようとするのが問題の趣旨である。
2 年生の女子である確率 Pr{B2 ∩ A} = 45 / 510 は,2 年生である確率 Pr{B2} = 121 / 510 と 2 年生であるという条件付きでの女子である確率 Pr{A | B2} = 45 / 121 を用いて乗法定理の ( 2 ) 式から,
Pr{B2 ∩ A}
= Pr{B2} ・ Pr{A | B2}
= 121 / 510 ・ 45 / 121
= 45 / 510 …… ( 4 )
である。
女子であるという条件付きでの 2 年生である確率 Pr{B2 | A} は,乗法定理の ( 1 ) 式から,
Pr{B2 | A}= Pr{B2 ∩ A}/ Pr{A}
であり,( 4 )式および,
Pr{A}
= Pr{B1 ∩ A} + Pr{B2 ∩ A} + Pr{B3 ∩ A} + Pr{B4 ∩ A}
= 36 / 510 + 45 / 510 + 43 / 510 + 39 / 510
= 163 / 510
であるから,
Pr{B2 | A}
= ( Pr{B2} ・ Pr{A | B2})/ Pr{A}
= (121 / 510 ・ 45 / 121)/(163 / 510)
= 0.2761
となる。
ベイズの定理
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/11 15:41 UTC 版)

|
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)
翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
| 統計学 |
| ベイズ統計学 |
|---|
| 理論 |
|
| 技法 |
|
| 確率論 |
|---|
 |

確率論や統計学において、トーマス・ベイズ牧師にちなんで名付けられたベイズの定理(ベイズのていり、英: Bayes' theorem)、ベイズの法則、最近ではベイズ・プライスの定理[1]とは、ある事象に関連する可能性のある条件についての事前の知識に基づいて、その事象の確率を記述するものである[2]。例えば、健康問題の発生リスクが年齢とともに増加することが知られている場合、ベイズの定理により、ある年齢の個人のリスクを、単にその個人が集団全体の典型的な例であると仮定するよりも、(年齢を条件として)より正確に評価することができる。
ベイズの定理を応用したものに、推計統計学の手法の一つであるベイズ推定がある。その際、定理に関わる確率は、異なる確率解釈をすることができる。ベイズ確率の解釈では、定理は確率として表現された信念の度合いが、関連する証拠の入手可能性を考慮して合理的にどのように変化すべきかを表現している。ベイジアン推論は、ベイズ統計学の基本である。



定理の説明
まず、確率 P(A) を考える。A は集合 Ω の部分集合とする。P とは、正定値性と加算性を満たし、P(Ω) = 1 を満たす関数である。(数学的には、およそ測度そのものである。)
次に、P(A | B) ≡ P(A ∩ B) / P(B) は条件付き確率の定義であり、元 x ∈ B が x ∈ A を満たす割合である。すなわち B を集合全体として部分集合 A ∩ B の確率を考えるということである。条件とは、Ω の部分集合 B を指定するための条件であり「条件を与える」というのと「部分集合 B を与える」のは等価である。
ベイズの定理は、次の式で表される[3]:
ベイズの定理
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/06/30 07:39 UTC 版)
現実世界で事象が発生した場合、通常、ある選択肢における選好が修正される。これは、選択肢を定義する事象に対して個人が抱く信念の度合いを修正することで行われる。 心臓治療の効果を調べる研究で、病院 j {\displaystyle j} の患者の生存確率を θ j {\displaystyle \theta _{j}} とする。生存確率 θ j {\displaystyle \theta _{j}} は、心臓病患者の生存率を高めると信じる人がいる事象 y {\displaystyle y} の発生で更新される。 イベント y {\displaystyle y} が発生した状況で、 θ j {\displaystyle \theta _{j}} について確率の記述を更新するには、 θ j {\displaystyle \theta _{j}} と y {\displaystyle y} の同時分布 P ( θ , y ) {\displaystyle P(\theta ,\,y)} を与えるモデルから始めなければならない。これは、事前分布 P ( θ ) {\displaystyle P(\theta )} とサンプリング分布 P ( y ∣ θ ) {\displaystyle P(y\mid \theta )} の積として記述することができる。 P ( θ , y ) = P ( θ ) P ( y ∣ θ ) {\displaystyle P(\theta ,y)=P(\theta )P(y\mid \theta )} 条件付き確率の基本性質から、事後分布は次のようになる。 P ( θ ∣ y ) = P ( θ , y ) P ( y ) = P ( y ∣ θ ) P ( θ ) P ( y ) {\displaystyle P(\theta \mid y)={\frac {P(\theta ,\,y)}{P(y)}}={\frac {P(y\mid \theta )\,P(\theta )}{P(y)}}} この条件付き確率と個々の事象との関係を示す式をベイズの定理という。この単純な表現の中に、更新された信念 P ( θ ∣ y ) {\displaystyle P(\theta \mid y)} を適切かつ解決可能な方法で組み込むことを目的とするベイズ推定の技術的核心が含まれている。
※この「ベイズの定理」の解説は、「ベイズ階層モデル」の解説の一部です。
「ベイズの定理」を含む「ベイズ階層モデル」の記事については、「ベイズ階層モデル」の概要を参照ください。
「ベイズの定理」の例文・使い方・用例・文例
- ベイズの定理のページへのリンク



