すい‐てい【推定】
推定 statistical inference
詳しくは,別のページを参照のこと。
推定
推定
推定
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/02/11 19:46 UTC 版)
推定(すいてい、英: presumption)とは、法律用語では、現状知り得た情報・傾向を元に、知り得ない事象を決めること。
概要
教会法、大陸法、英米法における推定
法学用語としての類推は、反証を許すか否かの別により、下記の二つに分けられる(ラテン語)。証拠収集(ディスカバリー)が重要であるとされ、そのための法制が整いつつある。
- Juris tantum - 「反証を許す推定」
- Juris et de jure - 「反証を許さない推定」
講学上の概念としての推定
講学上の概念としての「推定」は、「事実上の推定」と「法律上の推定」とに分けられる。
事実上の推定
Aという間接事実の存在が立証されたときにBという主要事実の存在についても確からしいと判断し、それを認定する裁判所又は裁判官の心証作用のこと。自由心証主義の帰結である。
民事裁判であっても、もし証拠保全命令、文書提出命令、調査嘱託などの申立てが認められ、証拠を入手して提出すれば、証拠調べが行われた上での推認が行われうる。もっとも、裁判所は証拠調べの必要性がないことを理由として命令を棄却することができ、これに対する抗告は認めていない[1]。判例を通じて規範化しているものもあることも否めない(私文書の印影から押印(本人又は代理人の意思に基づく捺印)を推定することなど)。
刑事裁判では、例えば「甲と乙は密室に入室した。中から怒鳴り声とわめき声が聞こえ、1分後に全身に血を浴びた甲が出てきたとき、乙は中で仰向けに血まみれになって横たわって死んでいた。」という証言や科学捜査の結果のあった事例において、「甲が乙を殺した」という要件事実が事実上推定されうる。
証明責任の転換を伴わないため、これを覆すには反証で足る。
法律上の推定
「法律上の推定」は、「法律上の事実推定」と「法律上の権利推定」(準用・類推適用)に分けられる。
法律上の事実推定
「事実Aがあるときは、事実Bと推定する」などの法令の規定によって、事実A(前提事実)の存在が立証されたときに要件事実B(推定事実)について証明責任を転換させる立法技術のこと。
法律上の権利推定
「事実Aがあるときは、権利Bがあるものと推定する」などの法令の規定によって、事実A(前提事実)の存在が立証されたときに権利Bの根拠となる事実について証明責任を転換させる立法技術のこと。
法令用語としての推定
法令用語としての「推定」は、主に「法律上の推定」の意味に用いられるが、暫定真実や法定証拠法則と解されることもある。これに対し、「みなす」は通常は擬制の意味である(「法律上の事実推定」と解されることもある)。
- 民法第32条の2(同時死亡の推定)
- 民法第186条(占有の態様等に関する推定)
- 民法第188条(占有物について行使する権利の適法の推定)
- 民法第250条(共有持分の割合の推定)
- 民法第420条(賠償額の予定)
- 民法第573条(代金の支払期限)
- 民法第772条(嫡出の推定)
- 会社法第120条(株主の権利の行使に関する利益の供与)
- 民事訴訟法第228条第4項(私文書の成立の真正の推定)
脚注
関連項目
推定
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/01/14 20:37 UTC 版)
現場の故障率レポートから、統計的な分析手法を用いて故障率を推定(estimation)することができる。正確な故障率を得るためには、分析者は機器の動作、データ収集の手順、故障率に影響を与える主要な環境変数、システムレベルでの機器の使用方法、およびシステム設計者による故障データの使用方法を十分に理解している必要がある。
※この「推定」の解説は、「故障率」の解説の一部です。
「推定」を含む「故障率」の記事については、「故障率」の概要を参照ください。
推定
「推定」の例文・使い方・用例・文例
- その化石は1万年前のものと推定された
- 法定推定相続人
- 彼はその土器の年代をおよそ1万年前のものと推定した
- もうすぐ株価は安定するだろうと推定されている
- 生存者はいないだろうという我々の推定は誤りだった
- 推定した結果が表1に示されている
- 発行または公表の事実が推定されます
- イギリスで冬を越すゴシキヒワの推定数は私の想像をはるかに超えていた。
- その問題について推定的に説明しなさい。
- このシステムの開発には100人月を要すると推定される。
- 彼の推定相続人は彼の一人娘である。
- マクロ環境分析に基づき来期の売上高を推定した。
- 日本の民法第772条は「妻が婚姻中懐胎した子は、夫の子と推定する」として、嫡出の推定を定めている。
- 過去の文献によれば、破裂のリスクはサイズにより推定される。
- 私はそれを推定します。
- 私たちはそのように推定します。
- それは立っていると推定された。
推定と同じ種類の言葉
品詞の分類
- >> 「推定」を含む用語の索引
- 推定のページへのリンク
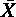 は
は




