ARCHモデル
ARCHモデル
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/03/24 06:05 UTC 版)
ナビゲーションに移動 検索に移動ARCHモデル(あーちモデル、英: autoregressive conditional heteroscedasticity model, ARCH model)とは、金融経済学、統計学、計量経済学などにおいて分散不均一性を示す時系列データに適用されるモデル。日本語では、「分散自己回帰モデル」「分散不均一モデル」等と称される。1982年にロバート・エングルによって提案された[1]。特に金融時系列データへの適用事例が多い。
目次
分散不均一性
株式の収益率をプロットすると、ある時期(景気が安定して拡大している時期など)には変動の程度(ボラティリティ)が平均して小さく、別の時期(不況の直前など)にはボラティリティが平均して大きくなる傾向が観察される。このようなボラティリティが時期によって異なった水準を示すことをボラティリティ・クラスタリング(英: volatility clustering)、または分散不均一性(英: heteroscedasticity)と呼ぶ。分散不均一性は金融時系列データをはじめ幅広く見られる現象である。
ARCH(q)モデル
時刻 における時系列データ の時刻 までの情報による条件付き期待値を とする。 と の差を とする。さらに
と分解できるとする。ただし は平均が0、分散が1の確率変数で、 はボラティリティであり、時刻 までの情報で確定していると考える。すなわち、時刻 の時点で、時刻 におけるこの時系列データのボラティリティは予測できる、と考えるのである。他方、 そのものは実際に時刻 になり確率変数 の値が確定するまでは確定しない。よって 自体は
と表せる。ARCH(q)モデルの下で条件付ボラティリティ は以下の式で決定される。
つまりARCH(q)モデルでは、q 期前までの平均からの乖離部分 の2乗が条件付きボラティリティに影響を与えている。仮定から であるのでARCHモデルの決定式は
と書き直すことが出来る。さらに は であることも分かる。つまり から見ると q 次の自己回帰モデルと見なせる。よって について自己回帰(英: autoregressive)であり、条件付き(英: conditional)ボラティリティ が分散不均一性(英: heteroscedasticity)を示すことから頭文字を取りARCHモデルと名付けられている。 についての定常性条件から次の についての方程式
の全ての解の絶対値が1より大きくなるように係数 に条件が課される場合が多い。
GARCH(p,q)モデル
1986年にロバート・エングルの弟子Tim BollerslevはARCHモデルを一般化したGARCHモデル(がーちモデル、英: Generalized ARCH model, GARCH model)を提案した[2]。GARCHモデルでは、条件付ボラティリティ は以下のように決定される。
すなわち、現在の条件付ボラティリティは p 期前までの条件付ボラティリティと q 期前までの平均からの乖離部分の2乗により決定される。Bollerslev も当該論文中の実証分析の節で述べているが、ARCHモデルを金融時系列データに適用すると分散の長期記憶性を再現する為に次数 q が大きくなる傾向があったが、GARCHモデルは比較的小さい次数(p = 1, q = 1)でも十分に分散の長期記憶性が再現されるので、ARCHモデルに比べると倹約的なモデルとなる。GARCHモデルにおいては は自己回帰移動平均モデルとして表され、その定常条件は
の全ての解の絶対値が1より大きくなることである。ただし かつ である。
GARCHモデルの拡張
GARCHモデルは様々な拡張がなされている。以下で代表的なものを述べる。
EGARCHモデル
Daniel B. Nelson が1991年に提案したExponential GARCH(p,q)モデル(EGRACH(p,q)モデル)は以下のようにボラティリティが決定する[3]。
EGARCHモデルにおいては通常のGARCHモデルと異なり、 ではなく、それを で割った がボラティリティに影響を与える。条件付き分散の対数に対してモデル化が行われているため、通常のGARCHモデルに比べると非負性や定常性のための制約が緩くなるという利点がある。
GJR GARCHモデル
Lawrence R. Glosten, Ravi Jagannathan, David E. Runkle によって1993年に提案されたGJR GARCHモデルは以下のようにボラティリティが決定する[4]。
ただし、 は が負ならば1、正ならば0を取る変数である。株価収益率などが持つ、下落局面でボラティリティがより増加するレバレッジ効果を捉えるためのモデルである。
Heston-Nandi GARCH モデル
Steven L. Heston, Saikat Nandi により2000年に提案されたHeston-Nandi GARCH(p,q)モデルは以下のようにボラティリティが決定する[5]。
Heston-Nandi GARCHモデルもEGARCHモデルと同様に ではなく がボラティリティに影響を与える。また、このモデルもGJR GARCHモデルと同様にレバレッジ効果を捉えることができる。さらにデリバティブのオプションと親和性が高く、Heston-Nandi GARCHモデルに従う株式のオプションについて、その無裁定価格が導出されている。しかし、Heston-Nandi GARCHモデルはモデルが過適合を起こしやすいという欠点もある。
多変数モデルへの拡張
ここまで述べてきたGARCHモデルはいずれも単一変数の時系列データに対して適用されるものであったが、多変数の時系列データに対してその相関構造を内包しつつ適用可能なGARCHモデルも存在する。例としてBEKKモデル[6]やCCC-GARCHモデル[7]、DCC-GARCHモデル[8]などがある。
脚注
- ^ Engle 1982
- ^ Bollerslev 1986
- ^ Nelson 1991
- ^ Glosten, Jagannathan and Runkle 1993
- ^ Heston and Nandi 2000
- ^ Engle and Kroner 1995
- ^ Bollerslev 1990
- ^ Engle 2002
参考文献
- Engle, Robert F. (1982), “Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation”, Econometrica 50 (4): 987-1007, JSTOR 1912773
- Bollerslev, Tim (1986), “Generalized autoregressive conditional heteroskedasticity”, Journal of Econometrics 31 (3): 307-327, doi:10.1016/0304-4076(86)90063-1
- Nelson, Daniel B. (1991), “Conditional heteroskedasticity in asset returns: A new approach”, Econometrica 59 (2): 347-370, JSTOR 2938260
- Glosten, Lawrence R.; Jagannathan, Ravi; Runkle, David E. (1993), “On the relation between the expected value and the volatility of the nominal excess return on stocks”, The Journal of Finance 48 (5): 1779-1801, doi:10.1111/j.1540-6261.1993.tb05128.x
- Heston, Steven L.; Nandi, Saikat (2000), “A closed-form GARCH option valuation model”, The Review of Financial Studies 13 (3): 585-625, doi:10.1093/rfs/13.3.585
- Engle, Robert F.; Kroner, Kenneth F. (1995), “Multivariate simultaneous generalized ARCH”, Econometric Theory 11 (1): 122-150, doi:10.1017/S0266466600009063
- Bollerslev, Tim (1990), “Modelling the coherence in short-run nominal exchange rates: A multivariate generalized ARCH model”, The Review of Economics and Statistics 72 (3): 498-505, JSTOR 2109358
- Engle, Robert F. (2002), “Dynamic conditional correlation: A simple class of multivariate generalized autoregressive conditional heteroskedasticity models”, Journal of Business and Economic Statistics 20 (3): 339-350, doi:10.1198/073500102288618487
関連項目
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ARCH(q)モデル
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/03/24 06:05 UTC 版)
「ARCHモデル」の記事における「ARCH(q)モデル」の解説
時刻 t {\displaystyle t} における時系列データ y t {\displaystyle y_{t}} の時刻 t − 1 {\displaystyle t-1} までの情報による条件付き期待値を μ t {\displaystyle \mu _{t}} とする。 y t {\displaystyle y_{t}} と μ t {\displaystyle \mu _{t}} の差を u t = y t − μ t {\displaystyle u_{t}=y_{t}-\mu _{t}} とする。さらに u t = σ t ε t {\displaystyle u_{t}=\sigma _{t}\varepsilon _{t}} と分解できるとする。ただし ε t {\displaystyle \varepsilon _{t}} は平均が0、分散が1の確率変数で、 σ t {\displaystyle \sigma _{t}} はボラティリティであり、時刻 t − 1 {\displaystyle t-1} までの情報で確定していると考える。すなわち、時刻 t − 1 {\displaystyle t-1} の時点で、時刻 t {\displaystyle t} におけるこの時系列データのボラティリティは予測できる、と考えるのである。他方、 u t {\displaystyle u_{t}} そのものは実際に時刻 t {\displaystyle t} になり確率変数 ε t {\displaystyle \varepsilon _{t}} の値が確定するまでは確定しない。よって y t {\displaystyle y_{t}} 自体は y t = μ t + u t = μ t + σ t ε t {\displaystyle y_{t}=\mu _{t}+u_{t}=\mu _{t}+\sigma _{t}\varepsilon _{t}} と表せる。ARCH(q)モデルの下で条件付ボラティリティ σ t {\displaystyle \sigma _{t}} は以下の式で決定される。 σ t 2 = α 0 + α 1 u t − 1 2 + ⋯ + α q u t − q 2 = α 0 + ∑ i = 1 q α i u t − i 2 {\displaystyle \sigma _{t}^{2}=\alpha _{0}+\alpha _{1}u_{t-1}^{2}+\cdots +\alpha _{q}u_{t-q}^{2}=\alpha _{0}+\sum _{i=1}^{q}\alpha _{i}u_{t-i}^{2}} つまりARCH(q)モデルでは、q 期前までの平均からの乖離部分 u t − i {\displaystyle u_{t-i}} の2乗が条件付きボラティリティに影響を与えている。仮定から v t = u t 2 − E t − 1 [ u t 2 ] = u t 2 − σ t 2 {\displaystyle v_{t}=u_{t}^{2}-E_{t-1}[u_{t}^{2}]=u_{t}^{2}-\sigma _{t}^{2}} であるのでARCHモデルの決定式は u t 2 = α 0 + ∑ i = 1 q α i u t − i 2 + v t {\displaystyle u_{t}^{2}=\alpha _{0}+\sum _{i=1}^{q}\alpha _{i}u_{t-i}^{2}+v_{t}} と書き直すことが出来る。さらに v t {\displaystyle v_{t}} は E [ u t − i 2 v t ] = 0 , i = 1 , … {\displaystyle E[u_{t-i}^{2}v_{t}]=0,\;i=1,\dots } であることも分かる。つまり u t 2 {\displaystyle u_{t}^{2}} から見ると q 次の自己回帰モデルと見なせる。よって u t 2 {\displaystyle u_{t}^{2}} について自己回帰(英: autoregressive)であり、条件付き(英: conditional)ボラティリティ σ t {\displaystyle \sigma _{t}} が分散不均一性(英: heteroscedasticity)を示すことから頭文字を取りARCHモデルと名付けられている。 u t 2 {\displaystyle u_{t}^{2}} についての定常性条件から次の z {\displaystyle z} についての方程式 1 − ∑ i = 1 q α i z i = 0 {\displaystyle 1-\sum _{i=1}^{q}\alpha _{i}z^{i}=0} の全ての解の絶対値が1より大きくなるように係数 α i , i = 1 , … , q {\displaystyle \alpha _{i},\;i=1,\dots ,q} に条件が課される場合が多い。
※この「ARCH(q)モデル」の解説は、「ARCHモデル」の解説の一部です。
「ARCH(q)モデル」を含む「ARCHモデル」の記事については、「ARCHモデル」の概要を参照ください。
- ARCHモデルのページへのリンク
 期の
期の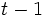 期までの
期までの











![{\displaystyle v_{t}=u_{t}^{2}-E_{t-1}[u_{t}^{2}]=u_{t}^{2}-\sigma _{t}^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8c353432a9bc094927a3a1a4898613c6965dd54e)


![{\displaystyle E[u_{t-i}^{2}v_{t}]=0,\;i=1,\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/44ea72a2675f9a72e1ddebfaca8f0f03a3f62707)








![{\displaystyle \log \sigma _{t}^{2}=\omega +\sum _{i=1}^{p}\beta _{i}\log \sigma _{t-i}^{2}+\sum _{i=1}^{q}{\Big (}\alpha _{i}\varepsilon _{t-i}+\gamma _{i}{\Big (}|\varepsilon _{t-i}|-E[|\varepsilon _{t-i}|]{\Big )}{\Big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d257acefae83499facdf6d97b7ec0d02e4a331a7)






