定常過程
定常過程
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/02/25 14:10 UTC 版)

|
この記事は英語版の対応するページを翻訳することにより充実させることができます。(2024年5月)
翻訳前に重要な指示を読むには右にある[表示]をクリックしてください。
|
概要
定常過程では平均や分散も(もしあれば)時間や位置によって変化しない。例えば、ホワイトノイズは定常的である。しかし、シンバルを鳴らしたときの音は定常的ではなく、時間と共に音が弱まっていく。
定常性(Stationarity)は時系列の解析でも重要であり、時系列データを定常的なものに変換することがよく行われる。例えば、経済的データは季節による変動があったり、価格レベルに依存する。ある定常過程と1つ以上の過程に傾向(トレンド)が認められるとき、これら過程を「傾向定常的; trend stationary」であるという。このようなデータから定常的成分だけを抜き出して分析することを「傾向除去; de-trending」と呼ぶ。
離散時間の定常過程で、標本値も離散的(とりうる値が N 個に限定されている)な場合をベルヌーイ系(Bernoulli scheme)と呼ぶ。N = 2 の場合を特にベルヌーイ過程(Bernoulli process)と呼ぶ。
弱い定常性
弱い定常性は確率過程の各時刻における期待値が時刻に依存せず、かつ、相関関数が時間差のみに依存するという条件で定義付けられる(⇒ #弱い定常性の定義、#弱い定常性の解釈)。
弱い定常性をもつ無作為信号を線型で時不変な(LTI)フィルタで処理するとき、相関関数を線型写像と考える。2つの引数の差にのみ依存するため、それは巡回演算子であり、その固有関数はフーリエ複素指数である。さらに、LTI演算子の固有関数も複素指数であり、弱い定常性をもつ無作為信号のLTI処理は非常に扱いやすい。全ての計算は周波数領域で実行できる。このため、弱い定常性仮定は信号処理アルゴリズムによく使われている。平均と共分散のある狭義の定常過程も弱い定常性をもつ。
弱い定常性の定義
弱い定常性の定義にあたり、以下のように記号を置く:
- 時刻
 カテゴリ
カテゴリ
定常過程と同じ種類の言葉
- 定常過程のページへのリンク
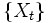
 と
と , および
, および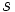
 と
と の
の
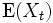 と
と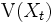 が
が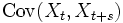 も
も 