ちょうわ‐へいきん〔テウワ‐〕【調和平均】
調和平均
調和平均
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/06/12 23:06 UTC 版)
数学において、調和平均(ちょうわへいきん、英: harmonic mean, subcontrary mean)とは、いくつかある広義の平均のうちの一つである。典型的には、率(割合・比率)の平均が望まれているような状況で調和平均が適切である。
正の実数について、調和平均は逆数の算術平均の逆数として定義される。例えば、3つの数 1, 2, 4 の調和平均は次のようになる:
-

2数 a, b の3種のピタゴラス平均の幾何学的構成。H によって示されている紫色の線が調和平均を表す。A, G はそれぞれ算術平均、幾何平均を表す。また、Q は二乗平均平方根を表す。 正の実数の集合に対して、調和平均を H, 算術平均を A, 幾何平均を G とすると、3つの平均の間には関係 H ≤ G ≤ A が成り立つ。平均を取る数の値がすべて等しいとき、かつそのときに限り、3つの平均は等しくなる。
また、2数 x1, x2 について考えると、調和平均は
-

h は A と B の調和平均の 1/2 である。 図のように、二つのはしごが通路の両端に立ててあり、高さ A および B の位置で脚とは反対側の壁に寄りかかっている場合を考える。このとき、はしごが交差する点の床からの高さ h は A と B の調和平均の 1/2 である。壁が斜めであっても、床からの各点の距離は壁との平行線を基準にすれば、A, B, h で変わらない。- 楕円において、semi-latus rectum(焦点から楕円への短軸に平行な直線に沿った距離)は焦点から楕円の最大と最小の距離の調和平均である。
- 三角関数において、タンジェントの二倍角の公式で、角 A について tan A = s/c と与えられていれば、tan 2A は、c, s の調和平均と、c − s の逆数の積である。数式で表現すれば
-
外部リンク
- 『調和平均』 - コトバンク
- 『調和平均にまつわる重要な公式まとめ』 - 高校数学の美しい物語
- Weisstein, Eric W. "Harmonic Mean". mathworld.wolfram.com (英語).
- Averages, Arithmetic and Harmonic Means at cut-the-knot
調和平均
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/05/05 03:37 UTC 版)
詳細は「調和平均」を参照 調和平均(ちょうわへいきん、英: harmonic mean)は μ H = n ∑ i = 1 n 1 x i = n 1 x 1 + 1 x 2 + ⋯ + 1 x n {\displaystyle \mu _{\mathrm {H} }={\frac {n}{\textstyle \sum \limits _{i=1}^{n}{\frac {1}{x_{i}}}}}={\frac {n}{{\tfrac {1}{x_{1}}}+{\tfrac {1}{x_{2}}}+\cdots +{\tfrac {1}{x_{n}}}}}} で定義される。あるいは n μ H = ∑ i = 1 n 1 x i = 1 x 1 + 1 x 2 + ⋯ + 1 x n {\displaystyle {\frac {n}{\mu _{\mathrm {H} }}}=\textstyle \sum \limits _{i=1}^{n}{\dfrac {1}{x_{i}}}={\dfrac {1}{x_{1}}}+{\dfrac {1}{x_{2}}}+\cdots +{\dfrac {1}{x_{n}}}} とも表せる。 調和平均は、逆数の算術平均の逆数である。あるいは、逆数の算術平均は調和平均の逆数である。 しかし、データに1つ以上の 0 があるとき、調和平均はもとの定義式からは定義できないが、0 への極限を取ると、調和平均は 0 となる( x i → 0 {\displaystyle x_{i}\to 0} のとき μ H → 0 {\displaystyle \mu _{\mathrm {H} }\to 0} )。データに負数があっても調和平均は計算することができる。ただし、正負が混在している場合に逆数の和が 0 になることがあり、その場合の極限は発散する。
※この「調和平均」の解説は、「平均」の解説の一部です。
「調和平均」を含む「平均」の記事については、「平均」の概要を参照ください。
調和平均
「調和平均」の例文・使い方・用例・文例
- 調和平均のページへのリンク
 を持つ
を持つ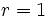 と
と


