偏相関係数

統計学用語辞典

偏相関係数

例題：
　「表 1 に示すデータにおいて，変数 Z の影響を取り除いたときの，変数 X と変数 Y の間の偏相関係数を求めなさい。」

表 1．三変数データ

X	Y	Z
61.0	52.0	58.0
57.3	44.2	45.7
55.5	63.3	62.6
40.8	29.5	28.0
27.9	46.8	52.5
57.0	50.6	67.1
57.5	41.6	49.1
47.7	67.8	51.6
57.1	43.1	54.4
56.6	47.8	44.9
43.7	46.4	39.0
61.7	60.0	62.1
32.0	45.7	45.0
44.4	49.3	38.3
50.1	65.3	50.9

説明
　2変数の相関関係を調べるとき，それぞれの変数が第3の変数と相関を持っていることにより，観察された相関が真の相関関係を表さないことがある。
　そこで，対象としている2変数以外の変数の影響を取り除いた相関係数を求めることが必要になることがある。
　p 個の変数があるとき，q 個の変数を固定した（影響を取り除いた）p-q 個の変数間の偏相関係数は「 q 次のオーダーの偏相関係数 」と呼ばれる。
　2 変数 i，j 間の相関係数を r(ij) とし，固定される変数を k1， k2， …， kq の q 個としたとき，2 変数 i，j 間の q 次のオーダーの偏相関係数は（1）式，（2）式の漸化式で 計算できる。
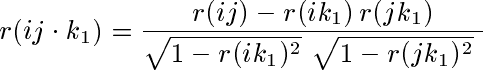　　……（1）
　　……（2）
（2）式では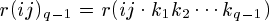， などと略記した。
　2 変数 i，j 以外の全ての変数を固定したときの偏相関係数は，相関係数行列 r の逆行列の要素を r^ij としたとき，（3）式で求めることができる。
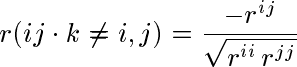　　……（3）
注
　3 変数の場合に，1 変数を固定した 2 変数間の偏相関係数を求めるとき，（1）式は複雑であるので（4）式の方がわかりやすいかもしれない。
　　……（4）


計算手順：

1. 2 変数間の相関係数は表 2 のようになる。引き続く計算誤差を少なくするために，相関係数は小数点以下の桁数を多めに計算する。
   

   表 2．相関係数行列

   	X	Y	Z
   X	1.00000
   Y	0.25058	1.00000
   Z	0.49484	0.59803	1.00000

2. （4）式を用いて偏相関係数を求める。
   ( 0.25058 - 0.49484 × 0.59803) / { √( 1 - 0.49484² ) × √( 1 - 0.59803² ) } ≒ -0.06511
   （注：コンピュータを用いて計算したときは，小数点以下5桁までの答えは -0.06512 である）。