偏回帰係数の求め方

統計学用語辞典

偏回帰係数の求め方

1. 有効ケース数を n とする。従属変数を Y，p 個の独立変数を Xi（ i = 1， 2， ... ， p ）とする。
   
2. 従属変数の予測値 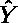は，重回帰式
   
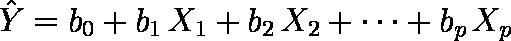
   により求められる。
   
3. 以下では図 1 のような独立変数が 2 個の場合を考えることにする。
   予測値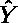 は予測平面
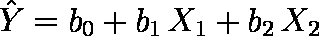
   上にある。
   

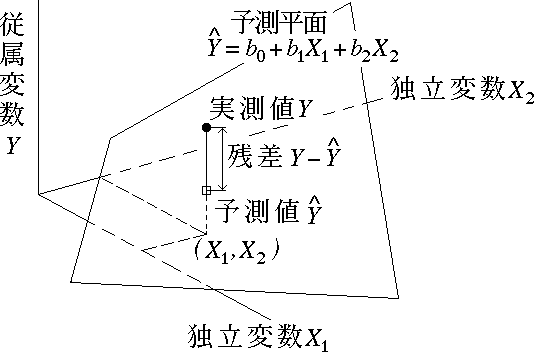
   図 1．独立変数が 2 個のときの重回帰分析の模式図

   
   
4. 実測値 Y との差（ 残差 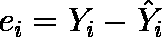） を最小にすればよさそうであるが，残差は正負の符号を持つので，その 2 乗和が最小になるように独立変数にかけられる重み bi（ 偏回帰係数 ）および定数項 b0 を定める。
   この手法を 最小二乗法 と呼び，得られる係数を 最小二乗推定値 と呼ぶ。
   　　…… ( 1 )
   
5. （ 1 ）式を，b0，b1，b2 で偏微分して 0 とおく。
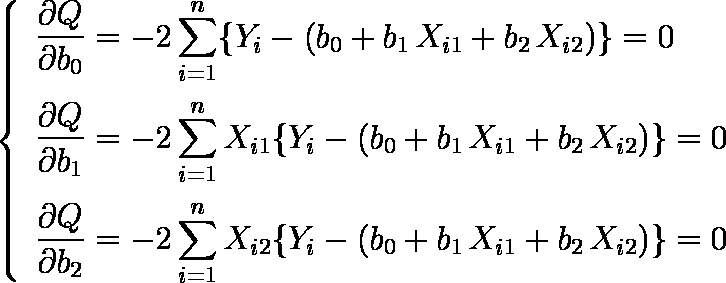   　　…… ( 2 )
   
6. （ 2 ）式に，変数 Y，X1，X2 の平均値を 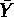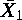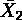，， としたときの関係式
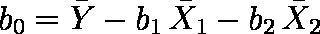   　　…… ( 3 )
   および，独立変数 Xi，Xj 間の変動・共変動
   
   および，独立変数 Xi と従属変数 Y の共変動
   
   を代入して整理すると，
   
   という連立方程式（ 正規方程式 と呼ぶ ）が得られる。
   これを解くことにより偏回帰係数 b1，b2 が求まる。
   
7. 一般的な表し方としては，
   
   1. 独立変数間の変動・共変動行列を S，独立変数と従属変数間の共変動ベクトルを c，偏回帰係数ベクトルを bとして，( 4 ) 式のようになる。
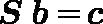      　　…… ( 4 )
      
   2. S の逆行列を S ^{- 1} とすれば，偏回帰係数は（ 5 ）式で求められる。
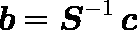      　　…… ( 5 )
   
   
8. 定数項 b0 は（ 3 ）式から求められる。
   
9. 重回帰分析の結果は，表 1 のようにまとめられる。
   

   表 1．重回帰分析結果の表示

   	偏回帰係数	標準誤差	t 値	P 値	標準化偏回帰係数
   X1	31.9670	6.840	4.673	＜0.001	0.620
   X2	48.0183	12.322	3.897	＜0.001	0.478
   X3	-29.536	11.990	2.463	0.018	-0.240
   X4	-454.373	171.514	2.649	0.011	-0.284
   定数項	594.562	789.895	0.753	0.456
   t 値の自由度は42