二群の代表値の差の検定(マン・ホィットニーの U 検定)
例題:
「表 1 のような観察値が得られた。両群の母代表値に差があるかどうか検定しなさい。」
| 第 1 群の観察値 | 1.2,1.5,1.8,2.6 |
|---|---|
| 第 2 群の観察値 | 1.3,1.9,2.9,3.1,3.9 |
R による解析:
> wilcox.test(c(1.2,1.5,1.8,2.6), c(1.3,1.9,2.9,3.1,3.9)) Wilcoxon rank sum test data: c(1.2, 1.5, 1.8, 2.6) and c(1.3, 1.9, 2.9, 3.1, 3.9) W = 4, p-value = 0.1905 alternative hypothesis: true mu is not equal to 0
二群の代表値の差の検定(マン・ホィットニーの U 検定)
例題:
「A,B 薬の治療効果を比較した結果が表 3 のように与えれれている。2 群の母代表値の差を有意水準 5% で両側検定しなさい。」
| 不変 | やや有効 | 有効 | 著効 | 合計 | |
|---|---|---|---|---|---|
| A薬投与群 | 9 | 12 | 6 | 3 | 30 |
| B薬投与群 | 4 | 9 | 11 | 5 | 29 |
R による解析:
# A <- c(rep(1, 9), rep(2, 12), rep(3, 6), rep(4, 3)) # A 薬 # B <- c(rep(1, 4), rep(2, 9), rep(3, 11), rep(4, 5)) # B 薬 A <- rep(1:4, c(9, 12, 6, 3)) B <- rep(1:4, c(4, 9, 11, 5)) > wilcox.test(A, B, correct=F) # correct=F は連続性の修正を行わないことを指示している。 Wilcoxon rank sum test
# 名前が違う別の検定のように見えるが,マン・ホイットニーの U 検定と等価な検定である。 data: A and B W = 310.5, p-value = 0.04883 alternative hypothesis: true mu is not equal to 0 Warning message: Cannot compute exact p-value with ties in: wilcox.test.default(A, B, correct = F) U の分散や,Z 値が表示されないので,自分で定義した関数を使ってみる > U.test(A, B, correct=F) U E(U) V(U) Z P value 3.105000e+02 4.350000e+02 3.993559e+03 1.970105e+00 4.882639e-02 > chisq.test(matrix(c(9,12,6,3,4,9,11,5),ncol=4,byrow=T))
# 分布の差の検定(独立性の検定)を行ってみる。 Pearson's Chi-squared test data: matrix(c(9, 12, 6, 3, 4, 9, 11, 5), ncol = 4, byrow = T) X-squared = 4.3065, df = 3, p-value = 0.2302 Warning message: Chi-squared approximation may be incorrect in:
chisq.test(matrix(c(9, 12, 6, 3, 4, 9, 11, 5), ncol = 4, byrow = T))
二群の代表値の差の検定(マン・ホィットニーの U 検定)
例題:
「表 1 のような観察値が得られた。両群の母代表値に差があるかどうか検定しなさい。」
| 第 1 群の観察値 | 1.2,1.5,1.8,2.6 |
|---|---|
| 第 2 群の観察値 | 1.3,1.9,2.9,3.1,3.9 |
検定手順:
- 前提
- 2 群のケース数をそれぞれ n1,n2,また,n = n1 + n2 とする。
例題では,n1 = 4,n2 = 5,n = 9 である。
- 2 群をこみにして観察値を小さい順に並べ,小さい方から順位をつける。
同順位がある場合には平均順位をつける。
例題では,表 2 のようになる。
表 2.順位付け 観察値 1.2 1.3 1.5 1.8 1.9 2.6 2.9 3.1 3.9 順位 1 2 3 4 5 6 7 8 9 群別 1 2 1 1 2 1 2 2 2
- 各群ごとに,付けられた順位の和 R1,R2 を求める。
例題では,
第 1 群に属する観察値に付けられた順位の和
R1 = 1 + 3 + 4 + 6 = 14
第 2 群に属する観察値に付けられた順位の和
R2 = 2 + 5 + 7 + 8 + 9 = 31
となる。
- 検定統計量 U1,U2 を求める。
U1 = n1 n2 + n1 (n1+1) / 2-R1
U2 = n1 n2 + n2 (n2+1) / 2-R2
注:並べ替えたり,平均順位をつけたりするのは面倒くさい。U 統計量を求める手順として別のやり方もある。
-
例題では,U1 = 16,U2 = 4 となる。
- 統計数値表を引く都合上,検定統計量は U0 = min(U1, U2) とする。
例題では,U0 = 4 である。
- 統計数値表が利用できるかどうかで,以下のいずれかを選択する。
- ケース数が小さい場合
- 統計数値表を参照して棄却限界値を求める。
例題では,5% の有意水準で検定を行うとき,棄却限界値は 1 である。
- 帰無仮説の採否を決める。
例題では,帰無仮説は採択される。すなわち,「2 群の母代表値に差があるとはいえない」といえる。
注:同順位がある場合には,統計数値表は使用できないので,「ケース数が大きい場合」の正規化検定を援用する。ただし,ケース数がある程度大きくなければ近似的な検定結果が得られるにすぎない。
- 統計数値表を参照して棄却限界値を求める。
- ケース数が大きい場合
- 検定統計量 U の平均値は E(U) = n1 n2 / 2,分散は V(U) = n1 n2 ( n + 1) / 12 ゆえ,次式の Z0 は,正規分布に従う。
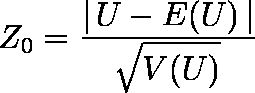
- 有意確率を P = Pr{| Z | ≧ Z0} とする。
正規分布表,または正規分布の上側確率の計算を参照すること。
- 帰無仮説の採否を決める。
注:同順位がある場合には,Z0 を求める式中の分散 V(U) を修正しなければならない。
同順位となる値が m 種類あり,それぞれの同順位となる値の数(同順位の大きさ)を ti(i = 1,2,... ,m)としたとき,分散 V(U) は次式で表される。
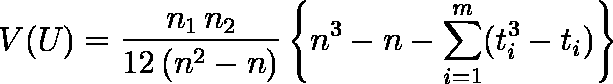
- 検定統計量 U の平均値は E(U) = n1 n2 / 2,分散は V(U) = n1 n2 ( n + 1) / 12 ゆえ,次式の Z0 は,正規分布に従う。
- ケース数が小さい場合
二群の代表値の差の検定と同じ種類の言葉
- 二群の代表値の差の検定のページへのリンク
