二群の比率の差の検定のとき
有意水準 α,検出力 1−β で二群の比率の差の検定を行うときに必要な標本の大きさを求める。
各群の比率を P1,P2 とし,プールした比率を P = ( P1 + P2 ) / 2 とする。
Q1 = 1 - P1, Q2 = 1 - P2,Q = 1 - P とする。
連続性の補正を行わないで両側検定を行うときに,各群に必要な標本の大きさ n の見積もりは,次式で求めることができる。
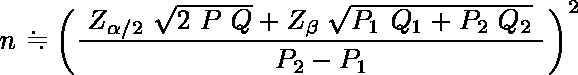
この式で,Zα/2,Zβ は標準正規分布のパーセント点である。
Zα/2 = Z0.05/2 = 1.9600
Zβ = Z0.20 = 0.8416 など
検定を行う際に連続性の補正を行うときは,以下のようにして修正する。
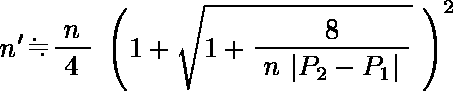
例:
旧薬,新薬の有効率が 80%,90% のとき,α = 0.05,β = 0.20 で両側検定を行うとき,n ≒ 198.96 なので,各群ごとに 199 例を用意することになる。なお,n' ≒ 237.3 である。
なお,この式は,両群のサンプル数が異なるときの式の特殊な場合として導かれている( 一般式は,浜島信之 「多変量解析による臨床研究」,名古屋大学出版会にもある )。
- 二群の比率の差の検定のときのページへのリンク
