二元配置分散分析
検定手順:
- 二要因 A,B の組合せによる測定値を,表 1 のように表す。
表 1. 二元配置分散分析の各セルの繰返し数と平均値 要因 B 水準 1 水準 2 … 水準 b ケース数合計 平均値 要因 A 水準 1 n11 n12 … n1b n1・ 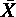 1・
1・水準 2 n21 n22 … n2b n2・ 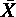 2・
2・: : : … : : : 水準 a na1 na2 … nab na・ 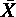 a・
a・ケース数
合計n・1 n・2 … n・b n・・ 平均値 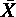 ・1
・1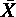 ・2
・2... 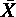 ・b
・b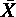 ・・
・・
- 前提
各セルのケース数により,以下の 4 つの方法のどれかにより検定を行う。
- 各水準の繰返し数が等しく,1 である場合
- 各水準の繰返し数が等しく,2 以上である場合
- 各水準の繰返し数が等しくないが,周辺度数に比例する場合
- 各水準の繰返し数が等しくなく,周辺度数にも比例しない場合
二元配置分散分析--各水準の繰返し数が等しく,1 である場合
例題:
「表 1 のようなデータがある。4 種の肥料間で収量に差があるか,また,3 種の品種ごとに差があるか検定しなさい。」
| 肥料 | ||||
|---|---|---|---|---|
| 品種 | B1 | B2 | B3 | B4 |
| A1 | 9 | 17 | 12 | 16 |
| A2 | 1 | 21 | 16 | 11 |
| A3 | 7 | 19 | 6 | 9 |
検定手順:
- 前提
- 帰無仮説 H0:「要因効果がない」。
- 対立仮説 H1:「要因効果がある」。
- 有意水準 α で両側検定を行う(片側検定は定義できない)。
注:意味的に両側検定である。形式的には F 分布の片側確率を使う片側検定である。
- 各セルの測定値を Xij( i = 1, 2, ... , a;j = 1, 2, ... , b )とする。
例題では,a = 3,b = 4 である。
- 分析対象変数 X の全変動 SSt は以下のように 3 個の独立な変動に分解できる。
全変動 = 要因 A の効果 + 要因 B の効果 + 残差
SSt = SSa + SSb + SSe
SSa と SSb はそれぞれ要因 A,要因 B の主効果とよばれる。この場合には交互作用はない。これは,乱塊法に他ならない。
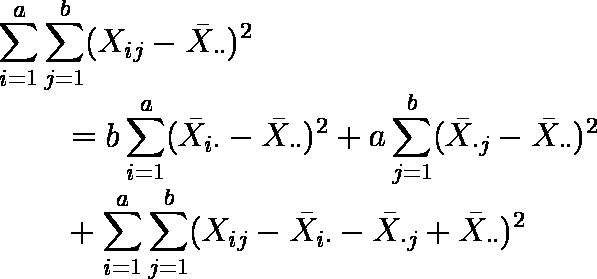
- 二元配置分散分析の結果は,表 2 のような分散分析表で表される。
表 2.分散分析表 - 1 変動要因 平方和 自由度 平均平方 F値 要因 A SSa dfa=a-1 MSa=SSa/dfa Fa=MSa/MSe 要因 B SSb dfb=b-1 MSb=SSb/dfb Fb=MSb/MSe 残差 SSe dfe=(a-1)(b-1) MSe=SSe/dfe 全体 SSt dft=ab-1
例題では,表 3 のようになる。表 3.例題に対する分散分析表 要因 平方和 自由度 平均平方 F 値 有意確率 品種 21.50000 2 10.75000 0.6592845 0.55103 肥料 268.6667 3 89.55556 5.492334 0.03719 残差 97.83333 6 16.30556 合計 388.0000 11 35.27273
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
- それぞれの自由度を持つ F 分布において,有意確率を P = Pr{F ≧ F0} とする。
F 分布表(α = 0.05,α = 0.025,α = 0.01,α = 0.005),または F 分布の上側確率の計算を参照すること。
例題では,品種の差については,自由度が(2,6)の F 分布において,Pr{F ≧ 5.14}= 0.05 であるから,P = Pr{F ≧ 0.659}> 0.05 である(正確な有意確率:P = 0.551)。
肥料の差については,自由度が(3,6)の F 分布において,Pr{F ≧ 4.76}= 0.05 であるから,P = Pr{F ≧ 5.492}< 0.05 である(正確な有意確率:P = 0.037)。
- 帰無仮説の採否を決める。
例題では,有意水準 5% で検定を行うとすれば(α = 0.05),品種の差においては P > α であるから,帰無仮説を採択する。すなわち,「品種の差があるとはいえない」とする。肥料の差においては P < α であるから,帰無仮説を棄却する。すなわち,「肥料の差がある」とする。
二元配置分散分析--各水準の繰返し数が等しく,2 以上である場合
例題:
「年齢と季節がホルモンの分泌量と関係するかどうかについて,年齢階級および各季節ごとにそれぞれ別々に 3 人ずつ,計 60 人の被検者のホルモン分泌量を測定した結果は表 1 のようになった。5% の有意水準で二元配置分散分析をしなさい。」
| 20〜24歳 | 25〜29歳 | 30〜34歳 | 35〜39歳 | 40〜45歳 | |
|---|---|---|---|---|---|
| 春 | 24.8 23.9 24.1 | 25.0 26.6 27.9 | 27.5 32.5 29.5 | 29.8 26.7 30.7 | 28.5 25.7 28.7 |
| 夏 | 28.8 22.6 28.0 | 28.5 27.1 25.2 | 26.3 28.2 31.8 | 28.5 26.5 26.7 | 31.3 29.4 29.8 |
| 秋 | 26.4 27.4 29.4 | 27.9 29.2 26.7 | 30.2 31.7 29.2 | 31.7 27.2 25.5 | 30.3 29.6 31.7 |
| 冬 | 30.0 28.7 29.2 | 25.0 29.9 29.4 | 30.3 30.9 28.4 | 29.9 27.3 28.8 | 33.6 32.0 34.3 |
検定手順:
- 前提
- 帰無仮説 H0:「要因効果がない」。
- 対立仮説 H1:「要因効果がある」。
- 有意水準 α で両側検定を行う(片側検定は定義できない)。
注:意味的に両側検定である。形式的には F 分布の片側確率を使う片側検定である。
- 繰返し数を n,各セルの測定値を Xijk(i=1,2,... ,a;j=1,2,... ,b;k=1,2,... ,n)とする。
例題では,n = 3,a = 4,b = 5 である。
- 表 2 の各水準の平均値は,
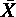 i . .,
i . .,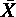 . j . のように “.” が最後にもう 1 個つき,それは各水準の組み合わせでの繰返し数 nij を意味する。また,
. j . のように “.” が最後にもう 1 個つき,それは各水準の組み合わせでの繰返し数 nij を意味する。また,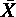 ij . は各水準の組み合わせでの平均値を意味する。
ij . は各水準の組み合わせでの平均値を意味する。
- この場合には,分析対象変数 X の全変動 SSt は以下のように 4 個の独立な変動に分解できる。
全変動 = 要因 A の効果 + 要因 B の効果 + 要因 A と要因 B の交互作用 + 残差
SSt = SSa + SSb + SSab + SSe
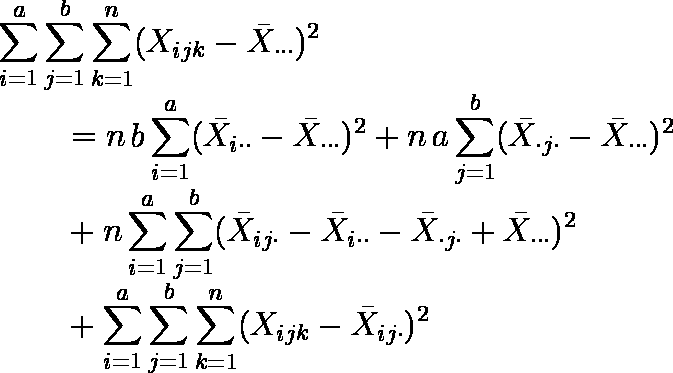
- この場合,二元配置分散分析は表 2 のような分散分析表で表される。
表 2.分散分析表 変動要因 平方和 自由度 平均平方 要因 A SSa dfa = a - 1 MSa = SSa / dfa 要因 B SSb dfb = b - 1 MSb = SSb / dfb 交互作用 SSab dfab = ( a - 1 ) ( b - 1 ) MSab = SSab / dfab 残差 SSe dfe = a b ( n - 1 ) MSe = SSe / dfe 全体 SSt dft = a b n - 1
表 3.分散分析表 を解釈する 3 つのモデル F 値 変動要因 モデルI モデルII 混合モデル 要因 A Fa = MSa / MSe MSa / MSab MSa / MSab 要因 B Fb = MSb / MSe MSb / MSab MSb / MSe 交互作用 Fab = MSab / MSe MSab / MSe MSab / MSe
モデル I は 母数モデル とも呼ばれる。要因 A,B の各水準を固定された不動のものとみなす。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fab が第 1 自由度が dfab,第 2 自由度が dfe である F 分布に従うことを利用する。
モデル II は 変量モデル とも呼ばれる。要因 A,B の各水準は無数の水準の内の標本とみなし,そこから得られる推測結論を,標本以外の広い範囲へも適用しようとするものである。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfab である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfab である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
混合モデル は,片方の要因に母数モデル,もう一方の要因に変量モデルを考えるものである。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfe である F 分布に従うことを利用する。
- それぞれの自由度を持つ F 分布において,有意確率を P = Pr{F ≧ F0} とする。
F 分布表(α = 0.05,α = 0.025,α = 0.01,α = 0.005),または F 分布の上側確率の計算を参照すること。
- 帰無仮説の採否を決める。
例題では,それぞれのモデルごとに以下のようになる。各表の右端の欄に帰無仮説を棄却するか採択するかを示す。
n.s. は有意確率が 0.05 以上なので,帰無仮説を採択する。
* は有意確率が 0.05 以下なので,帰無仮説を棄却する。
** は有意確率が 0.01 以下なので,帰無仮説を棄却する。
表 4.モデル I( 母数モデル ) 要因 平方和 自由度 平均平方 F値 有意確率 季節 51.39733 3 17.13244 4.937067 0.00520 ** 年齢 106.2873 4 26.57183 7.657221 0.00011 ** 交互作用 52.85267 12 4.404389 1.269215 0.27389 n.s. 残差 138.8067 40 3.470167 合計 349.3440 59 5.921085
表 5.モデル II( 変量モデル ) 要因 平方和 自由度 平均平方 F値 有意確率 季節 51.39733 3 17.13244 3.889857 0.03739 * 年齢 106.2873 4 26.57183 6.033035 0.00672 ** 交互作用 52.85267 12 4.404389 1.269215 0.27389 n.s. 残差 138.8067 40 3.470167 合計 349.3440 59 5.921085
二元配置分散分析--周辺度数に比例する場合
例題:
「表 1 のようなデータについて二元配置分散分析を行いなさい。」
| 要因 B | ||||||
|---|---|---|---|---|---|---|
| b1 | b2 | b3 | b4 | b5 | ||
| 要因 A | a1 | 7.0 5.7 | 4.6 5.6 | 7.0 7.4 6.6 | 7.3 6.3 7.8 | 5.3 4.7 |
| a2 | 5.8 8.9 | 10 7.1 | 6.5 9.8 5.0 | 9.7 6.4 9.9 | 7.8 5.4 | |
| a3 | 8.1 6.1 10.2 6.9 | 5.2 5.7 11.8 6.1 | 10.4 5.6 9.4 5.9 12.1 5.7 | 5.3 9.7 5.5 10.2 13.8 7.0 | 11.1 4.2 7.1 5.0 | |
検定手順:
- 前提
- 帰無仮説 H0:「要因効果がない」。
- 対立仮説 H1:「要因効果がある」。
- 有意水準 α で両側検定を行う(片側検定は定義できない)。
注:意味的に両側検定である。形式的には F 分布の片側確率を使う片側検定である。
- 分析対象変数 X の全変動 SSt は,次式のように 4 個の独立な変動に分解できる。
全変動 = 要因 A の効果 + 要因 B の効果 + 要因 A と要因 B の交互作用 + 残差
SSt = SSa + SSb + SSab + SSe
SSa と SSb はそれぞれ要因 A,要因 B の主効果とよばれる。
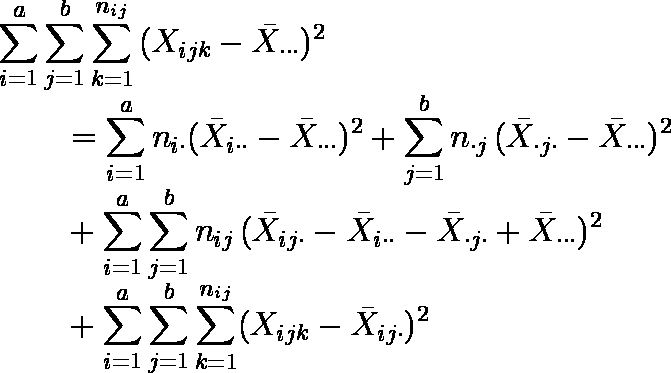
- この場合,二元配置分散分析は表 2 のような分散分析表で表される。
表 2.分散分析表 変動要因 平方和 自由度 平均平方 要因 A SSa dfa = a - 1 MSa = SSa / dfa 要因 B SSb dfb = b - 1 MSb = SSb / dfb 交互作用 SSab dfab = ( a - 1 ) ( b - 1 ) MSab = SSab / dfab 残差 SSe dfe = n・・- a b MSe = SSe / dfe 全体 SSt dft = n・・ - 1
表 3.分散分析表 を解釈する 3 つのモデル F 値 変動要因 モデルI モデルII 混合モデル 要因 A Fa = MSa / MSe MSa / MSab MSa / MSab 要因 B Fb = MSb / MSe MSb / MSab MSb / MSe 交互作用 Fab = MSab / MSe MSab / MSe MSab / MSe
モデル I は 母数モデル とも呼ばれる。要因 A,B の各水準を固定された不動のものとみなす。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fab が第 1 自由度が dfab,第 2 自由度が dfe である F 分布に従うことを利用する。
モデル II は 変量モデル とも呼ばれる。要因 A,B の各水準は無数の水準の内の標本とみなし,そこから得られる推測結論を,標本以外の広い範囲へも適用しようとするものである。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfab である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfab である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
混合モデル は,片方の要因に母数モデル,もう一方の要因に変量モデルを考えるものである。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfab である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fb が第 1 自由度が dfb,第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 A の有意性の検定は,Fa が第 1 自由度が dfa,第 2 自由度が dfe である F 分布に従うことを利用する。
- それぞれの自由度を持つ F 分布において,有意確率を P = Pr{F ≧ F0} とする。
F 分布表(α = 0.05,α = 0.025,α = 0.01,α = 0.005),または F 分布の上側確率の計算を参照すること。
- 帰無仮説の採否を決める。
例題では,それぞれのモデルごとに以下のようになる。各表の右端の欄に帰無仮説を棄却するか採択するかを示す。
n.s. は有意確率が 0.05 以上なので,帰無仮説を採択する。
* は有意確率が 0.05 以下なので,帰無仮説を棄却する。
** は有意確率が 0.01 以下なので,帰無仮説を棄却する。
表 4.モデル I( 母数モデル ) 要因 平方和 自由度 平均平方 F 値 有意確率 要因 A 20.79688 2 10.39844 1.758991 0.18798 n.s. 要因 B 19.53646 4 4.884115 0.8261929 0.51804 n.s. 交互作用 7.848958 8 0.9811198 0.1659654 0.99400 n.s. 残差 195.0825 33 5.911591 合計 243.2648 47 5.175847
表 5.モデル II( 変量モデル ) 要因 平方和 自由度 平均平方 F 値 有意確率 要因 A 20.79688 2 10.39844 10.59854 0.00564 ** 要因 B 19.53646 4 4.884115 4.978102 0.02600 * 交互作用 7.848958 8 0.9811198 0.1659654 0.99400 n.s. 残差 195.0825 33 5.911591 合計 243.2648 47 5.175847
表 6.混合モデル 要因 平方和 自由度 平均平方 F 値 有意確率 要因 A 20.79688 2 10.39844 10.59854 0.00564 ** 要因 B 19.53646 4 4.884115 0.8261929 0.51804 n.s. 交互作用 7.848958 8 0.9811198 0.1659654 0.99400 n.s. 残差 195.0825 33 5.911591 合計 243.2648 47 5.175847
二元配置分散分析--周辺度数にも比例しない場合
二元配置分散分析において,「各水準の繰返し数が等しくなく,周辺度数にも比例しない」という状況は,データ採取後に 2 要因でケースを 2 重分類して要因効果を検討するような場合には最もありうる。
このようなものを,非直交要因計画といい,要因の主効果が互に独立ではなく,交互作用も主効果と独立ではないので平方和( 変動 )の加法性はそのままでは成立しない。要因間に因果的順序がなく,主効果は交互作用よりはるかに大きい場合( 古典的要因計画法 )には以下のように分析が行われる。
例題:
「表 1 のデータについて二元配置分散分析を行いなさい。」
| 要因 B | |||
|---|---|---|---|
| b1 | b2 | ||
| 要因 A | a1 | 17 16 | 25 22 |
| a2 | 18 26 | 34 30 34 30 | |
検定手順:
- 前提
- 帰無仮説 H0:「要因効果がない」。
- 対立仮説 H1:「要因効果がある」。
- 有意水準 α で両側検定を行う(片側検定は定義できない)。
注:意味的に両側検定である。形式的には F 分布の片側確率を使う片側検定である。
- 解析対象変数の変動が SSt である。
例題では,SSt = 415.6 である。
- 分析対象変数 X の全変動 SSt は,次式のように 4 個の独立な変動に分解できる。
全変動 = 要因 A の効果 + 要因 B の効果 + 要因 A と要因 B の交互作用 + 残差
二元配置分散分析の結果は,表 2 のような分散分析表で表される。
表 2.分散分析表 変動要因 平方和 自由度 平均平方 F値 要因 A SSa・b dfa・b = a - 1 MSa・b = SSa・b / dfa・b Fa・b = MSa・b / MSe 要因 B SSb・a dfb・a = b - 1 MSb・a = SSb・a / dfb・a Fb・a = MSb・a / MSe 交互作用 SSab dfab = ( a - 1 ) ( b - 1 ) MSab = SSab / dfab Fab = MSab / MSe 残差 SSe dfe = n・・ - a b MSe = SSe / dfe 全体 SSt dft = n・・ - 1
- 2 要因の加法的効果を SSa,b としたとき 2 要因は非直交であるから,SSa,b ≠ SSa + SSb である( したがって,SSa + SSb + SSab + SSe ≠ SSt である )。そこで,SSa,b のうち要因 B で説明されない部分を要因 A に割当て,要因 A で説明されない部分を要因 B に割当てる。具体的には,各要因についてダミー変数を用いた重回帰分析を行い,対応する変動を抽出する。
例題では,要因 A,B の水準の数はそれぞれ 2 であるので,主効果を表すダミー変数はそれぞれ 1 個ずつ考えればよい。水準 1 の場合に 1,水準 2 の場合に 0 を取るようなダミー変数を考える。また,交互作用を表すダミー変数も 1 個考えればよく,要因 A,B とも水準 1 の場合に 1,そうでない場合に 0 を取るようなダミー変数を考える。
重回帰分析に用いるデータ行列は表 3 のようになる。
表 3.重回帰分析に用いるデータ行列 水準 観察値
(従属変数)ダミー変数(独立変数) 要因A 要因B A の主効果 B の主効果 A, Bの 交互作用 1 1 17 1 1 1 1 1 16 1 1 1 1 2 25 1 0 0 1 2 22 1 0 0 2 1 18 0 1 0 2 1 26 0 1 0 2 2 34 0 0 0 2 2 30 0 0 0 2 2 34 0 0 0 2 2 30 0 0 0
- 要因 A,B およびその交互作用を表す( a - 1 ) + ( b - 1 ) + ( a - 1 )( b - 1 )個のダミー変数を独立変数とし,解析対象変数を従属変数とした重回帰分析を行う。これは「飽和モデル」であり,2 つの要因の全ての効果を抽出するものである。重回帰分散分析表の残差平方和の項が SSe である。全てのダミー変数によって説明される平方和の項が SSa,b,ab である。SSt = SSa,b,ab + SSe という関係が成り立つ。
例題では,飽和モデルとして,A の主効果,B の主効果,A, B の交互作用を表す 3 つのダミー変数を独立変数として重回帰分析を行う。
表 4 から,残差平方和 SSe = 53.0 を得る。
また,回帰により説明される平方和は SSa,b,ab = 362.6 である。
表 4.飽和モデルの
回帰分析における分散分析表要因 平方和 自由度 平均平方 F値 回帰 362.6000 3 120.8667 13.68302 残差 53.00000 6 8.833333 全体 415.6000 9
- 要因 A,B を表す( a - 1 ) + ( b - 1 )個のダミー変数を独立変数とし,解析対象変数を従属変数とした重回帰分析を行う。これは要因 A と B の「加法モデル」である。全てのダミー変数によって説明される平方和の項は SSa,bである。
例題では,要因 A と B の加法モデルとして,A の主効果,B の主効果を表す 2 つのダミー変数を独立変数として重回帰分析を行う。
表 5 の回帰により説明される平方和は SSa,b = 357.4571 である。
表 5.加法モデルの
回帰分析における分散分析表要因 平方和 自由度 平均平方 F値 回帰 357.4571 2 178.7286 21.51769 残差 58.14286 7 8.306122 全体 415.6000 9
- 要因 A,B の交互作用は,SSab = SSa,b,ab - SSa,b で定義する。
例題では,表 4 の回帰により説明される平方和( SSa,b,ab = 362.6 )と,表 5 の回帰により説明される平方和( SSa,b = 357.4571 )の差( 5.142857 )が,交互作用の平方和 SSab = 362.6 - 357.4571 = 5.1429 である。
- 要因 A を表す( a - 1 )個のダミー変数を独立変数とし,解析対象変数を従属変数とした重回帰分析を行う。全てのダミー変数によって説明される平方和の項は要因 A の主効果 SSaである。
例題では,要因 A を表す 1 つのダミー変数を独立変数として重回帰分析を行う。
表 6 の回帰により説明される平方和が SSa = 180.2667 である。
表 6.要因 A の
回帰分析における分散分析表要因 平方和 自由度 平均平方 F値 回帰 180.2667 1 180.2667 6.128045 残差 235.3333 8 29.41667 全体 415.6000 9
- 要因 B を表す( b - 1 )個のダミー変数を独立変数とし,解析対象変数を従属変数とした重回帰分析を行う。全てのダミー変数によって説明される平方和の項は要因 B の主効果 SSbである。
例題では,要因 B を表す 1 つのダミー変数を独立変数として重回帰分析を行う。
表 7 の回帰により説明される平方和が SSb = 236.0167 である。
表 7.要因 B の
回帰分析における分散分析表要因 平方和 自由度 平均平方 F値 回帰 236.0167 1 236.0167 10.51397 残差 179.5833 8 22.44792 全体 415.6000 9
- 加法モデルにより説明される変動のうち,要因 B で説明されない部分を,「B で調整された A の主効果」として SSa ・ b = SSa,b - SSb で定義する。
例題では,表 5 の回帰により説明される平方和( SSa,b = 357.4571 )と,表 7 の回帰により説明される平方和( SSb = 236.0167 )の差が,SSa ・ b = 357.4571 - 236.0167 = 121.4404 である。
- 加法モデルにより説明される変動のうち,要因 A で説明されない部分を,「A で調整された B の主効果」として SSb ・ a = SSa,b - SSa で定義する。
例題では,表 7 の回帰により説明される平方和( SSa,b = 357.4571 )と,表 6 の回帰により説明される平方和( SSa = 180.2667 )の差が SSb ・ a = 357.4571 - 180.2667 = 177.1904 である。
- 要因 A の有意性の検定は,Fa・b が第 1 自由度が dfa・b,第 2 自由度が dfe である F 分布に従うことを利用する。
- 要因 B の有意性の検定は,Fb・a が第 1 自由度が dfb・a,第 2 自由度が dfe である F 分布に従うことを利用する。
- 交互作用 の有意性の検定は,Fab が第 1 自由度が dfab,第 2 自由度が dfe である F 分布に従うことを利用する。
- それぞれの自由度を持つ F 分布において,有意確率を P = Pr{F ≧ F0} とする。
F 分布表(α = 0.05,α = 0.025,α = 0.01,α = 0.005),または F 分布の上側確率の計算を参照すること。
- 以上をまとめて分散分析表を完成させる。
例題では,表 8 のようになる。
表 8.表 1 のデータに対する分散分析表 - モデル I( 母数モデル ) 要因 平方和 自由度 平均平方 F値 有意確率 要因 A SSa・b 121.4405 1 121.4405 13.74798 0.01000 要因 B SSb・a 177.1905 1 177.1905 20.05930 0.00420 交互作用 SSab 5.142857 1 5.142857 0.5822102 0.47437 残差 SSe 53.00000 6 8.833333 合計 SSt 415.6000 9 46.17778
- 帰無仮説の採否を決める。
例題では,有意水準 5% で検定を行うとすれば(α = 0.05),要因 A の効果は, P < α であるから,帰無仮説を棄却する。すなわち,「要因効果がある」とする。要因 B の効果は, P < α であるから,帰無仮説を棄却する。すなわち,「要因効果がある」とする。交互作用は, P > α であるから,帰無仮説を採択する。すなわち,「交互作用があるとはいえない」とする。
二元配置分散分析と同じ種類の言葉
- 二元配置分散分析のページへのリンク
