乱塊法

統計学用語辞典

乱塊法

例題：
　「表 1 のようなデータがある。4 種の肥料間で収量に差があるか，また，3 種の品種ごとに差があるか検定しなさい。」

表 1．乱塊法が対象とするデータ

	肥料
品種	B1	B2	B3	B4
A1	9	17	12	16
A2	1	21	16	11
A3	7	19	6	9

R による解析

> randblk(dat)	# この関数の定義を見る
                   SS d.f.       MS   F value    P value
Treatment   268.66667    3 89.55556 5.4923339 0.03719245
Replication  21.50000    2 10.75000 0.6592845 0.55102999
Residual     97.83333    6 16.30556        NA         NA
Total       388.00000   11 35.27273        NA         NA

aov 関数を用いる場合

> m <- matrix(c(9,1,7,17,21,19,12,16,6,16,11,9),3,4)
> m
     [,1] [,2] [,3] [,4]
[1,]    9   17   12   16
[2,]    1   21   16   11
[3,]    7   19    6    9
> df <- data.frame(x=as.vector(m), Treatment=as.factor(col(m)), Replication=as.factor(row(m)))
> df
    x Treatment  Replication
1   9         1            1
2   1         1            2
3   7         1            3
4  17         2            1
5  21         2            2
6  19         2            3
7  12         3            1
8  16         3            2
9   6         3            3
10 16         4            1
11 11         4            2
12  9         4            3
> summary(aov(x ~ Treatment + Replication, df))
             Df  Sum Sq Mean Sq F value  Pr(>F)  
Treatment     3 268.667  89.556  5.4923 0.03719 *
Replication   2  21.500  10.750  0.6593 0.55103  
Residuals     6  97.833  16.306                  
---
Signif. codes:  0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1  

乱塊法

例題：
　「8 名のボランティアを被検者として，ある薬剤を投与しない場合（0mg），10，20，40，80mg 投与する場合の 5 通りの処置を行い，効果を測定した結果は表 5 のようになった。薬剤の効果があるかどうかを 5% の有意水準で検定しなさい。」

表 5．薬剤投与量による効果

	投与量
被検者	0mg	10mg	20mg	40mg	80mg
1	5	60	35	62	76
2	24	44	74	63	76
3	56	57	70	74	79
4	44	51	55	23	84
5	8	68	50	24	64
6	32	66	45	63	46
7	25	38	70	58	77
8	48	24	40	80	72

R による解析

> randblk(dat)	# この関数の定義を見る
                  SS d.f.        MS   F value     P value
Treatment    7076.75    4 1769.1875 6.2886477 0.000965823
Replication  1771.50    7  253.0714 0.8995525 0.520523332
Residual     7877.25   28  281.3304        NA          NA
Total       16725.50   39  428.8590        NA          NA

乱塊法

　乱塊法は，対応のあるデータにおける平均値の差の検定である。
　乱塊法は農事研究における圃場試験での伝統的な呼び方であり，表 1 のようなデータを対象としている。


例題：
　「表 1 のようなデータがある。4 種の肥料間で収量に差があるか，また，3 種の品種ごとに差があるか検定しなさい。」

表 1．乱塊法が対象とするデータ

	肥料
品種	B1	B2	B3	B4
A1	9	17	12	16
A2	1	21	16	11
A3	7	19	6	9

検定手順:

1. 前提
   • 帰無仮説 H0：「母平均値の差はない」。
   • 対立仮説 H1：「母平均値に差がある」。
   • 有意水準 α で両側検定を行う（片側検定も定義できない）。
   
   
2. r 人の各被験者に c 種の処理を行い，測定値 Xij（i = 1，2，... ，r；j=1，2，... ，c）を得たとする。この場合の被験者（一般的には c 種類の処理が施される単位）をブロックと呼ぶ。
   

   表 2．乱塊法の記号表現

   被験者	処理1	処理2	…	処理c
   1	X11	X12	…	X1c
   2	X21	X22	…	X2c
   ：	：	：	：	：
   r	Xr1	Xr2	…	Xrc

   
   
3. 全体の平均を μ，処理 j の平均を μ・j，個体 i の平均を μi・，誤差を εij とすると次式のように表せる。
   
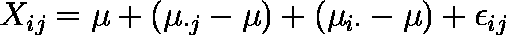
   または，
   
   
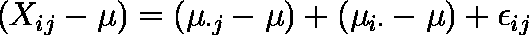
4. μ，μ・j ，μi・ に標本値 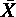・・ 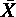，・j 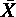，i・ をあてると，次式になる。
   
   
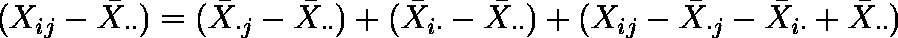
5. 式の両辺を 2 乗して i，j について和を求めると，次式が得られる。
   
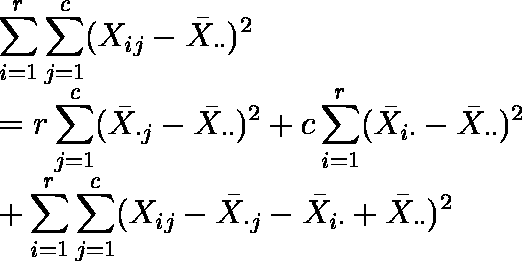
   この式は，測定値の全変動 SSt が，処理の差 SSt と個体の差 SSr および残差 SSe に分解されることを表している。
   
   
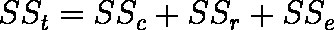
6. 乱塊法の解析結果を表 3 のような分散分析表で表す。
   

   表 4．乱塊法の分散分析表

   変動要因	平方和	自由度	平均平方	F 値
   処理の差	SSc	c - 1	MSc	MSc / MSe
   個体の差	SSr	r - 1	MSr	MSr / MSe
   残差（誤差）	SSe	( c - 1) ( r - 1 )	MSe
   全体	SSt	c r - 1	MSt

   MSc ，MSr ，MSe ，MSt は，対応する平方和を自由度で割ったもの
   

   表 5．表 1 のデータの乱塊法による分散分析

   	肥料
   品種	B1	B2	B3	B4	平均値
   A1	9	17	12	16	13.500
   A2	1	21	16	11	12.250
   A3	7	19	6	9	10.250
   平均値	5.667	19.000	11.333	12.000	12.000

   
   

   偏差平方

   9.000	25.000	0.000	16.000	2.250
   121.000	81.000	16.000	1.000	0.063
   25.000	49.000	36.000	9.000	3.063
   40.111	49.000	0.444	0.000

   
   

   分散分析表

   要因	平方和	自由度	平均平方	F 値	有意確率
   肥料の差	268.667	3	89.556	5.492	0.037
   品種の差	21.500	2	10.750	0.659	0.551
   残差	97.833	6	16.306
   全体	388.000	11	35.273

   
   
7. 処理間の有意差の検定は，MSc / MSe が，第 1 自由度 c - 1，第 2 自由度 が ( c - 1 ) ( r - 1 ) の F 分布に従うことを利用する。
   例題では，肥料の差についての検定統計量は F0 = 5.492 で，自由度（3，6）の F 分布に従う。
   
8. 個体間の有意差の検定は，MSr / MSe が，第 1 自由度 r - 1，第 2 自由度 が ( c - 1 ) ( r - 1 ) の F 分布に従うことを利用する。
   例題では，肥料の差についての検定統計量は F0 = 0.659 で，自由度（2，6）の F 分布に従う。
   
9. それぞれの自由度を持つ F 分布において，有意確率を P = Pr｛F ≧ F0｝ とする。
   F 分布表（α = 0.05，α = 0.025，α = 0.01，α = 0.005），または F 分布の上側確率の計算を参照すること。
   例題では，肥料の差については，自由度が（3，6）の F 分布において，Pr｛F ≧ 4.76｝= 0.05　であるから，P = Pr｛F ≧ 5.492｝＜ 0.05 である（正確な有意確率：P = 0.037）。
   品種の差については，自由度が（2，6）の F 分布において，Pr｛F ≧ 5.14｝= 0.05　であるから，P = Pr｛F ≧ 0.659｝＞ 0.05 である（正確な有意確率：P = 0.551）。
   
10. 帰無仮説の採否を決める。
    
    • P ＞ α のとき，帰無仮説を採択する。「母平均値に差があるとはいえない」。
    • P ≦ α のとき，帰無仮説を棄却する。「母平均値に差がある」。
    
    例題では，有意水準 5% で検定を行うとすれば（α = 0.05），肥料の差においては P ＜ α であるから，帰無仮説を棄却する。すなわち，「肥料の差はある」とする。品種の差においては P ＞ α であるから，帰無仮説を採択する。すなわち，「品種の差はない」とする。

ウィキペディア

乱塊法

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/10/27 01:03 UTC 版)

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "乱塊法" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2024年10月)

乱塊法とはフィッシャーの3原則である無作為化、反復、局所管理のすべてを取り入れた実験デザインである。

検定精度

完全無作為化法と比較すると、乱塊法は誤差分散が小さくなるため検定精度が高くなる。しかし、乱塊法は誤差の自由度が低くなるため、一般的に誤差の自由度を10以上確保できる場面で乱塊法を選択する方が有利になると考えられる。

外部リンク

• 乱塊法　randomized block design

表 話 編 歴 統計学
標本調査	標本 母集団 無作為抽出 層化抽出法
記述統計学	連続データ 位置 平均 算術 幾何 調和 中央値 分位数 順序統計量 最頻値 階級値 分散 範囲 偏差 偏差値 標準偏差 標準誤差 変動係数 決定係数 相関係数 自己相関 共分散 自己共分散 分散共分散行列 百分率 統計的ばらつき モーメント 分散 歪度 尖度 カテゴリデータ 頻度 分割表
推計統計学	仮説検定 パラメトリック t検定 ウェルチのt検定 F検定 Z検定 二項検定 ジャック–ベラ検定 シャピロ–ウィルク検定 分散分析 共分散分析 ノンパラメトリック ウィルコクソンの符号順位検定 マン・ホイットニーのU検定 カイ二乗検定 イェイツのカイ二乗検定 累積カイ二乗検定 フィッシャーの正確確率検定 尤度比検定 G検定 アンダーソン–ダーリング検定 コルモゴロフ–スミルノフ検定 カイパー検定 マンテル検定 コクラン・マンテル・ヘンツェルの統計量 その他 帰無仮説 対立仮説 有意 棄却 区間推定 信頼区間 予測区間 モデル選択基準 AIC BIC WAIC MDL その他 偏り 偏りと分散 過剰適合 推定量 点推定 最尤推定 尤度関数 尤度方程式 最小距離推定 メタアナリシス ブートストラップ法
ベイズ統計学	確率 主観確率 ベイズ確率 事前確率 事後確率 最大事後確率 その他 ベイズ推定 ベイズ因子
相関	相関係数 ピアソンの積率相関係数 スピアマンの順位相関係数 ケンドールの順位相関係数 偏相関係数 その他 自己相関 空間的自己相関 相互相関 交絡変数 相関関係と因果関係 擬似相関 錯誤相関
モデル	一般線形モデル 一般化線形モデル 混合モデル 一般化線形混合モデル
回帰	線形 リッジ回帰 ラッソ回帰 エラスティックネット 非線形 k近傍法 回帰木 ランダムフォレスト ニューラルネットワーク サポートベクター回帰 射影追跡回帰 時系列 自己回帰モデル 自己回帰移動平均モデル ARCHモデル 対移動平均比率法 トレンド定常 傾向推定 共和分 構造変化
分類	線形 線形判別分析 ロジスティック回帰 単純ベイズ分類器 単純パーセプトロン 線形サポートベクターマシン 二次 二次判別分析 非線形 k近傍法 決定木 ランダムフォレスト ニューラルネットワーク サポートベクターマシン ベイジアンネットワーク 隠れマルコフモデル その他 二項分類 多クラス分類 第一種過誤と第二種過誤
教師なし学習	クラスタリング k平均法（k-means++法） DBSCAN 密度推定（英語版） カーネル密度推定（カーネル） その他 主成分分析 独立成分分析 自己組織化写像
統計図表	棒グラフ バイプロット（英語版） 箱ひげ図 管理図 フォレストプロット ヒストグラム 円グラフ Q-Qプロット ランチャート 散布図 幹葉図 バイオリン図 ドットプロット ヒートマップ 階級区分図
生存時間分析	生存時間関数 カプラン＝マイヤー推定量 ログランク検定 故障率 比例ハザードモデル
歴史	統計学の創始者 確率論と統計学の歩み
応用	社会統計学 疫学 生物統計学 系統学 統計力学 計量経済学 機械学習 実験計画法
出版物	統計学に関する学術誌一覧 重要な出版物
全般	統計 頻度主義統計学 統計学および機械学習の評価指標
その他	方向統計学 S言語 R言語 統計検定 社会調査士 JDLA Deep Learning For GENERAL JDLA Deep Learning for ENGINEER 実用数学技能検定 品質管理検定
カテゴリ