名義尺度間の相関
2 個の変数 A,B がそれぞれ k 個,m 個のカテゴリーを持つとしたとき,k × m 個の桝目を持つ集計表(相関関係を見るときには特に相関表ともいう)を作成する。
| 要因 B | ||||||||
|---|---|---|---|---|---|---|---|---|
| B1 | B2 | ... | Bj | ... | Bm | 合計 | ||
| 要因 A | A1 | O1j | n1・ | |||||
| A2 | O2j | n2・ | ||||||
| : | : | : | ||||||
| Ai | Oi1 | Oi2 | ... | Oij | ... | Oim | ni・ | |
| : | : | : | ||||||
| Ak | Okj | nk・ | ||||||
| 合計 | n・1 | n・2 | ... | n・j | ... | n・m | n | |
表 1 のような k × m 分割表で,変数 A の第 i カテゴリー,変数 B の第 j カテゴリーの観察値を Oij とする。また,ni ・ を第 i 行の合計,n・ j を第 j 列の合計とする。
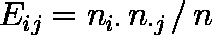
全ての桝目について ( Oij - Eij ) 2 / Eij の合計をとったものを χ20 とする (これは,独立性の検定に使用される)。
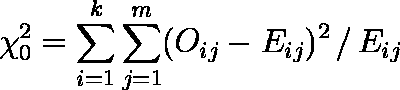
2 変数間の関連の強さは,χ20 から計算され,表 2 に示すようないくつかの指標がある。これらを総称して,属性相関係数と呼ぶ。
- ファイ係数 φ は,2 × 2 分割表に適用された場合には,ピアソンの積率相関係数(の絶対値)に一致する。
φ 係数は分割表の大きさ t = min ( k ,m ) により上限が異なるので,t の異なる分割表の間で関連の強さの比較ができない。
- コンティンジェンシー係数 C は,分割表の大きさ t が無限大になった場合には上限が 1 になるが,やはり t の異なる分割表の間で関連の強さの比較ができない。
- クラメール係数 V は,分割表の大きさに関係なく,0 から 1 の範囲の値をとるので,最も望ましいものといえる。
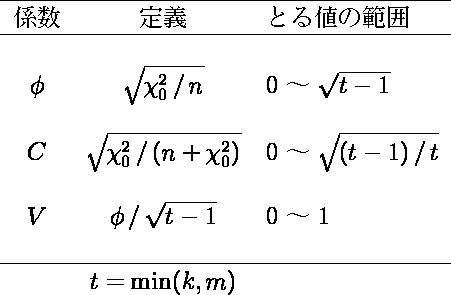 |
名義尺度間の相関と同じ種類の言葉
- 名義尺度間の相関のページへのリンク
