母平均の検定

統計学用語辞典

母平均の検定

例題：
　「31 人の身長の平均値が 157.8 cm，不偏分散が 24.6 であった。母平均が 156.2 cm であるかどうかを，有意水準 5% で検定しなさい。」


R による解析:

> boheikin.test(31, 157.8, 156.2, 24.6)	# この関数の定義を見る
          t        d.f.     P value 
 1.79611143 30.00000000  0.08255481 

母平均の検定

例題：
　「31 人の身長の平均値が 157.8 cm，不偏分散が 24.6 であった。母集団については，母平均 156.2 cm，母分散 = 25.5 であることが分かっているとする。標本平均は母平均と異なるといえるか有意水準 5% で検定しなさい。」


R による解析:

> boheikin.test(31, 157.8, 156.2, 25.5, known.sigma2=T)	# この関数の定義を見る
         z    P value 
1.76413063 0.07770999 

母平均の検定

例題：
　「31 人の身長の平均値が 157.8 cm，不偏分散が 24.6 であった。母平均が 156.2 cm であるかどうかを，有意水準 5% で検定しなさい。」


検定手順:

1. 前提
   • 帰無仮説 H0：「μ=μ0（母平均はμ0である）」。
   • 対立仮説 H1：「μ≠μ0（母平均はμ0ではない）」。
   • 有意水準 α で両側検定を行う（片側検定も定義できる）。
   
   
2. 母分散が既知か未知かでいずれかの方法をとる。
   
   • 母分散が未知の場合
     
     1. 母平均，ケース数，標本平均，標本不偏分散を，それぞれ μ0，n，，U とする。
        例題では，μ0 =　156.2，n = 31， = 157.8，U = 24.6 である（σ² は不明である）。
        
     2. 次式で t0 検定統計量を計算する。
        
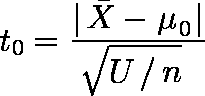
        例題では，t0 = 1.796 である。
        
     3. t0 は，自由度が n - 1 の t 分布に従う。
        例題では，自由度が 30 の t 分布に従う。
        
     4. 有意確率を P = Pr｛｜t｜ ≧ t0｝ とする。
        t 分布表，またはt 分布の両側確率の計算を参照すること。
        例題では，自由度 30 の t 分布において，Pr｛｜t｜≧ 2.042｝= 0.05 であるから，P = Pr｛｜t｜≧ 1.796｝＞ 0.05 である（正確な有意確率：P = 0.0825）。
     
     
   • 母分散が既知の場合
     
     1. 母平均，母分散，ケース数，標本平均を，それぞれ μ0，σ²，n， とする。
        
     2. 次式で Z0 検定統計量を計算する。
        
        
     3. Z0 は，正規分布に従う。
        
     4. 有意確率を P = Pr｛｜Z｜ ≧ Z0｝ とする。
        正規分布表，または正規分布の上側確率の計算を参照すること。
   
   
3. 帰無仮説の採否を決める。
   
   • P ＞ α のとき，帰無仮説を採択する。「母平均はμ0ではないとはいえない」。
   • P ≦ α のとき，帰無仮説を棄却する。「母平均はμ0ではない」。
   
   例題では，有意水準 5% で検定を行うとすれば（α = 0.05），P ＞ α であるから，帰無仮説を採択する。すなわち，「母平均 は156.2 cm でないとはいえない」といえる。

ウィキペディア小見出し辞書

母平均の検定

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/12/06 04:44 UTC 版)

「科学的方法」の記事における「母平均の検定」の解説

◆例1-1:母分散が既知の場合 ある病気の患者16人の血清中のカルシウム濃度の平均値(μ)は、7.4 mg/dlであった。健常者の血清中のカルシウム濃度は平均9.8 mg/dl(μ0) 標準偏差は0.5 mg/dlである。この時、H1：「この病気に感染すると血清中のカルシウム濃度は低下する」と言えるか？ 両側z検定において、有意水準pで帰無仮説を棄却することを考えた場合、p=0.05,p=0.01の場合の帰無仮説の採択範囲は以下のようになる。 α=0.05のとき、「=NORMSINV(0.05/2)」の計算値(Excel)は、「-1.959963985」であるため、標準正規分布の対称性より-1.96≦Z≦1.96となり、 α=0.01のとき、「=NORMSINV(-0.05/2)」の計算値(Excel)は、「0.005」であるため、標準正規分布の対称性より-0.005≦Z≦0.005 標本平均 μ = 7.4 に対し、検定統計量として標準化変数（Z）を以下のように定義する。 Z = μ − μ 0 σ n 前提よりZは（確率変数 μ について）標準正規分布N(0,1)に従う。実際に本例で標準化変数の値を計算すると以下の値を得る。 Z=-19.2 従って、p=0.05の場合でも,p=0.01の場合でも、この場合の標準化変数（Z）の値は、帰無仮説の採択範囲の採択範囲の外にあるため、帰無仮説はp=0.05でも、p=0.01でも棄却される。したがって、p=0.05でも、p=0.01でも「この病気に感染すると血清中のカルシウム濃度は低下する」と言える。 参考までに、(両側)Z検定においては,p値は、標準正規分布の累積分布関数(NORM.S.DIST)を用いて、この場合(Z=19.2の場合)は、 =2*(1-NORM.S.DIST(ABS(19.2),TRUE)) にて計算されるが、Excelにおいては、19.2は標準正規分布の標準偏差に対し離れすぎているため、桁落ちにて0と算出されてしまう。 ◆例1-2:母分散が未知の場合 W社に勤務する社員30名の血圧の平均値は145 mmHgで、不偏分散(U2)は900となった。血圧の全国平均は140 mmHgである。この時H1:「W社の社員の血圧は、全国平均に対し高い」と言えるか？ 自由度29の両側t検定において、検定において、有意水準pで帰無仮説を棄却することを考えた場合、p=0.05,p=0.01の場合の帰無仮説の採択範囲は以下のようになる。 p=0.05のとき、「=TINV(0.05,29)」の計算値(Excel)は、「2.045229642」でありt分布の対称性より、-2.05≦T≦2.05 p=0.01のとき、「=TINV(0.01,29)」の計算値(Excel)は、「2.756385904」でありt分布の対称性より、-2.76≦T≦2.76 題意より、標本数n=30,標本平均 μ = 145 mmHg であり、不偏分散は、 U n 2 = 1 n − 1 ∑ i = 1 n ( X i − X ¯ n ) 2 = 900 である。検定統計量として以下のスチューデント比(T)を次のように定義すると、 T = μ − μ 0 U n / n 前提より、Tは、自由度n-1のt分布に従う。実際に本例でスチューデント比(T)の値を計算すると、 T=0.912870929 である。 従って、p=0.05の場合でも、p=0.01の場合でも、上記のスチューデント比(T)の値はこの場合、帰無仮説の採択範囲の採択範囲の内にあるため、帰無仮説はp=0.05でも、p=0.01でも棄却されない。従って、p=0.01でもp=0.05でも、「W社の社員の血圧は、全国平均に対し高い」とは言えない。