マクネマー検定
例題:
「内閣の支持率調査で,同じ対象者に 1 月と 4 月の 2 回調査をした結果は表 1 のようになった。 この 3 ヵ月間に支持率に変化があったといえるかどうか検定しなさい。」
| 4 月 | ||||
|---|---|---|---|---|
| 支持する | 支持しない | 合計 | ||
| 1 月 | 支持する | 48 | 28 | 76 |
| 支持しない | 35 | 53 | 88 | |
| 合計 | 83 | 81 | 164 | |
R による解析:
> mcnemar.test(matrix(c(48,28,35,53),2,2), correct=F) # 連続性の補正をしない場合 McNemar's Chi-squared test data: matrix(c(48, 28, 35, 53), 2, 2) McNemar's chi-squared = 0.7778, df = 1, p-value = 0.3778 > mcnemar.test(matrix(c(48,28,35,53),2,2)) # 連続性の補正をする場合 McNemar's Chi-squared test with continuity correction data: matrix(c(48, 28, 35, 53), 2, 2) McNemar's chi-squared = 0.5714, df = 1, p-value = 0.4497 > binom.test(c(35,28)) # 二項検定による正確な有意確率 Exact binomial test data: 35 and 63 number of successes = 35, number of trials = 63, p-value = 0.45 alternative hypothesis: true probability of success is not equal to 0.5 95 percent confidence interval: 0.4248876 0.6808269 sample estimates: probability of success 0.5555556
マクネマー検定
例題:
「ある意見への賛否の態度を 2 回調査した結果は表 1 のようになった。 変化があったといえるかどうか検定しなさい。」
| 4 月 | |||||
|---|---|---|---|---|---|
| 支持する | どちらともいえない | 支持しない | 合計 | ||
| 1 月 | 支持する | 13 | 6 | 1 | 20 |
| どちらともいえない | 2 | 8 | 19 | 29 | |
| 支持しない | 4 | 7 | 21 | 32 | |
| 合計 | 19 | 21 | 41 | 78 | |
R による解析:
> tbl <- matrix(c( + 13, 6, 1, + 2, 8, 19, + 4, 7, 21 + ), ncol=3, byrow=T) > tbl [,1] [,2] [,3] [1,] 13 6 1 [2,] 2 8 19 [3,] 4 7 21 前もって定義されている関数を使う場合 > mcnemar.test(tbl) McNemar's Chi-squared test data: tbl McNemar's chi-squared = 9.3385, df = 3, p-value = 0.02511 別の拡張による新たに定義した関数を使う場合 > McNemar(tbl) n1 n2 P value 13.00000000 26.00000000 0.05325191
マクネマー検定
対応のある場合の比率の差の検定を行う。
例題:
「内閣の支持率調査で,同じ対象者に 1 月と 4 月の 2 回調査をした結果は表 1 のようになった。 この 3 ヵ月間に支持率に変化があったといえるかどうか検定しなさい。」
| 4 月 | ||||
|---|---|---|---|---|
| 支持する | 支持しない | 合計 | ||
| 1 月 | 支持する | 48 | 28 | 76 |
| 支持しない | 35 | 53 | 88 | |
| 合計 | 83 | 81 | 164 | |
検定手順:
- 記号を以下のように決める。
表 2.同じ対象者に行われた 2 回の内閣支持率調査結果 条件 2 特性を持つ 特性を持たない 合計 条件 1 特性を持つ a b a+b 特性を持たない c d c+d 合計 a+c b+d n
- 前提
- 標本比率の差は,( b - c ) / n である。帰無仮説のもとでは,b = c である。
これは,ケース数 = b + c,母比率 = 1/2 の場合の二項検定(母比率の検定)である。
b + c が大きい場合には,χ2 分布で近似できる。この検定法を特にマクネマーの検定と呼ぶ。
例題では,b = 28,c = 35 である。1 月,4 月における比率はそれぞれ 0.463,0.506 である。
- 状況に応じて以下のいずれかの方法により有意確率を求める。
- b + c が大きい場合(マクネマーの検定)
- 次式により検定統計量を計算する。
χ20 = ( b - c ) 2 / ( b + c )
連続性の補正を行うときは次式を使う。
χ20 = (|b - c|- 1) 2 / ( b + c)
ただし,b = c のときは χ20 = 0 とする。
例題では,b + c は十分に大きいので,マクネマーの検定を適用できる。
χ20 ≒ 0.778 となる(連続性の補正を行った場合は,χ20 ≒ 0.571)。
- χ20 は,自由度が 1 の χ2 分布に従う。
- 有意確率を P = Pr{χ2 ≧ χ20}とする。
χ2 分布表,または χ2 分布の上側確率の計算を参照すること。
例題では,自由度 1 の χ2 分布において,Pr{χ2 ≧ 3.84}= 0.05 であるから,P = Pr{χ2 ≧ 0.77}> 0.05 である(正確な有意確率:P = 0.378)。
連続性の補正を行ったときは,正確な有意確率は P = 0.450 となる。
- 次式により検定統計量を計算する。
- b + c が小さい場合(二項検定)
N = b + c,m = min (b, c) とすると,有意確率 P は,二項分布に基づいて次式で計算される。
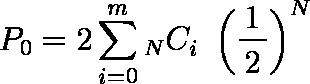
例題ではマクネマー検定でよいが,二項検定はいつの場合でも適用できる。有意確率は,P = 0.450 となる。
なお,二項検定はF 分布による母比率の検定と等価である。
- b + c が大きい場合(マクネマーの検定)
- 帰無仮説の採否を決める。
例題では,有意水準 5% で検定を行うとすれば(α = 0.05),P > α であるから,帰無仮説を採択する。すなわち,「支持率に変化があったとはいえない」。
マクネマー検定
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/03/02 21:49 UTC 版)
マクネマー検定(マクネマーけんてい、McNemar's test)は、統計学において、対応のある名目データに用いられる仮説検定である。 二値変数に関するマッチドペアの2x2分割表に適用され、行と列の限界度数が正しいかどうか(限界均一性があるかどうか)を判定する。1947年に導入したクイン・マクネマーにちなんで名付けられた[1]。遺伝学における応用例として、連鎖不平衡を検出するための伝達不平衡検定がある[2]。
医学分野では、主に感度(病気の人を正しく識別する能力)と特異度(病気のない人を正しく識別する能力)によって検査を評価する。同じグループの患者に対して2つのテストを行い、その感度と特異度が同じであれば両方の検査が同等であると考えがちだが、そうではないかもしれない。このため、私たちは病気のある患者と病気のない患者を調査したり、これら2つのテストが一致しない部分を見つけたりする必要がある。これがまさにマクネマーの検定の基礎であり、同じグループの患者に対する2つの診断テストの感度と特異度を比較する[3]。
定義
この検定は、n 人の被験者の標本に対する 2 つの検査の結果の 2x2分割表に、次のように適用される。
| 検査2 陽性 | 検査2 陰性 | 行合計 | |
| 検査1 陽性 | a | b | a + b |
| 検査1 陰性 | c | d | c + d |
| 列合計 | a + c | b + d | N |
限界均一性の帰無仮説とは、各結果に対する2つの限界確率が同じであるというもので、pa + pb = pa + pc かつ pc + pd = pb + pd に対応する。
したがって、帰無仮説H0と対立仮説H1は[1]
マクネマー検定と同じ種類の言葉
- マクネマー検定のページへのリンク
