数理計画問題
最適化問題
(数理計画問題 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/09 08:54 UTC 版)
最適化問題(さいてきかもんだい、英: optimization problem)とは、特定の集合上で定義された実数値関数または整数値関数についてその値が最小(もしくは最大)となる状態を解析する問題である[1]。こうした問題は総称して数理計画問題(すうりけいかくもんだい、英: mathematical programming problem, mathematical program)、数理計画とも呼ばれる[1]。最適化問題は、自然科学、工学、社会科学などの多種多様な分野で発生する基本的な問題の一つであり、その歴史は18世紀の変分問題に遡る[2]。1940年代に線型計画法が登場して以来、理論的な研究や数値解法の研究が非常に活発に行われ、その応用範囲はいろいろな分野に拡大されていった[1]。実世界の現象の数理的な解析に関わる問題や抽象的な理論の多くをこの最適化問題という一般的なくくりに入れることができる。物理学やコンピュータビジョンにおける最適化問題は、考えている関数をモデル化された系のエネルギーを表すものと見なすことによって、エネルギー最小化問題と呼ばれることもある。
定義
最適化問題を数学的に記述すると、最小化問題の場合
-
与えられた関数

Optimization computes maxima and minima.
| 一般 | |
|---|---|
| 微分可能 |
| 凸最小化 | |||||||
|---|---|---|---|---|---|---|---|
| 線形 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
||||
| ネットワークフロー (最大流問題) |
- 数理計画問題のページへのリンク
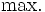
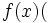 あるいは,
あるいは, 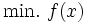 )
)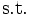
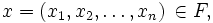
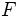 は
は 
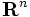 の
の は
は 


