モンテカルロ‐ほう〔‐ハフ〕【モンテカルロ法】
モンテカルロ法
モンテカルロ法
モンテカルロ法
別名:モンテカルロ解析
【英】Monte Carlo method
モンテカルロ法とは、確率論的問題を解析するための手法で、大量の乱数を用いて何度もシミュレーションを行なうことによって近似解を求める計算手法のことである。
モンテカルロ法では、対象となる条件式に、コンピュータで発生させた乱数をあてはめる操作を繰り返すことによって様々な解のサンプルを大量に採取していく。解析的な手法によって解を得ることが困難な問題でも、膨大な量のシミュレーションを繰り返すことによって、解の値に接近してゆくことができる。
モンテカルロ法には、精度の高い近似解を得ようとすればするほど膨大な回数の計算が必要になるという困難があった。コンピュータによって多量の乱数を生成し、多量の演算を短時間で処理し、演算結果の統計まで行ってしまうことによって、非常に効率的な解析を可能とした。
モンテカルロ法は第二次大戦中、コンピューターの父と呼ばれるジョン・フォン・ノイマン(John Luis von Neumann)によって、中性子の物質中を動き回る様子を探るために考案されたといわれている。なお、当初から通称として呼ばれていたモンテカルロの名は、モナコ公国の首都モンテカルロにちなんだものであると言われている。
モンテカルロ法
モンテカルロ法 Monte Carlo Method
モンテカルロ法
【英】:Monte Carlo method
概要
乱数を使って実験する方法のこと. 第二次世界大戦中に原爆の開発に関する極秘プロジェクトを示す符丁として, フォンノイマン等がカジノで有名なモンテカルロに因んで命名したとされている.本来は, 確率的な変動を含まない問題を解くのに乱数を利用する方法のことであったが, 現在では乱数を使う実験の総称として使われることが多い.
詳説
システムの特性値などを推定するために, 適当なモデルと乱数を使って実験し, 大数の法則や中心極限定理などを利用して推測を行う方法のこと. システムに確率的な変動が内在する場合だけでなく, 確定的な問題を解くためにも使われる.
モンテカルロ法の原理を簡単な例で示そう. 推定したい特性値を 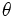 とし, これは既知の分布関数
とし, これは既知の分布関数  を持つ確率変数
を持つ確率変数  の関数
の関数 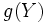 の平均値に等しいものとすれば,
の平均値に等しいものとすれば,
![\theta = E[g(Y)]=\int_{-\infty}^\infty g(y)\mathrm{d}F(y) =
\int_0^1 h(u) \mathrm{d}u, \,](https://cdn.weblio.jp/e7/img/dict/orjtn/b051904e001a6e946471c5f0d903dc80.png)
と書ける. ただし, 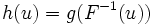 である. そこで, 区間[0,1]上の一様乱数
である. そこで, 区間[0,1]上の一様乱数 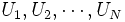 を発生し, 算術平均
を発生し, 算術平均
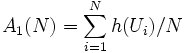
を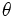 の推定値とすることが考えられる.
の推定値とすることが考えられる. 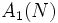 は
は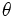 の不偏推定量であり, 分散は
の不偏推定量であり, 分散は
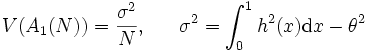
となる. したがって, 推定量 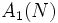 に含まれる誤差の標準偏差は
に含まれる誤差の標準偏差は 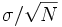 であり, 精度を十進で1桁上げるためには, サンプル数
であり, 精度を十進で1桁上げるためには, サンプル数  を10倍に増やさなければならない. このように, モンテカルロ法の収束は遅いので, これを改善するための方法が種々提案されており, 分散減少法と総称されている. ただし, これらは
を10倍に増やさなければならない. このように, モンテカルロ法の収束は遅いので, これを改善するための方法が種々提案されており, 分散減少法と総称されている. ただし, これらは 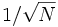 というオーダーを改善するものではなく, 比例係数を小さくするための工夫である.
というオーダーを改善するものではなく, 比例係数を小さくするための工夫である.
[重点サンプリング]
積分区間から一様にサンプルをとるのではなく, 重要と考えられる部分(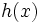 の絶対値が大きい部分)により多くの重みをおく密度関数
の絶対値が大きい部分)により多くの重みをおく密度関数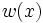 に従う乱数
に従う乱数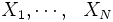 を発生し,
を発生し,
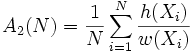
で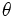 を推定する.
を推定する. 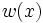 が
が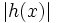 に比例するように選べれば分散は最小となるので, なるべくそれに近くなるように工夫する.
に比例するように選べれば分散は最小となるので, なるべくそれに近くなるように工夫する.
[制御変量法]
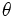 に対するひとつの不偏推定量を
に対するひとつの不偏推定量を とする.
とする.  と相関があって平均値
と相関があって平均値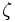 が既知の確率変数
が既知の確率変数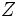 のことを,
のことを,  の制御変量という.
の制御変量という. 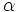 を定数として
を定数として
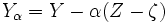
と定義すれば, 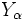 も
も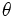 の不偏推定量となり, その分散は
の不偏推定量となり, その分散は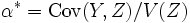 のとき最小となり, 最小値は
のとき最小となり, 最小値は
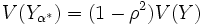
である. ここで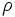 は
は と
と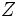 の相関係数であるから,
の相関係数であるから,  と相関の強い制御変量を選ぶほど効果的である.
と相関の強い制御変量を選ぶほど効果的である.
定積分の例では, 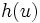 に近い関数
に近い関数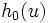 で, その積分の値
で, その積分の値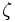 が正確に計算できるものを選び,
が正確に計算できるものを選び,
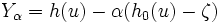
[負相関変量法]
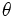 の不偏推定量
の不偏推定量 と平均値が同じで負の相関を持つ変量
と平均値が同じで負の相関を持つ変量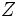 を利用して,
を利用して, 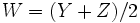 を
を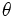 の推定量とする. この分散は,
の推定量とする. この分散は,  に対して2回独立にサンプルをとって平均する場合の分散より小さくなる. 定積分の例では, もし
に対して2回独立にサンプルをとって平均する場合の分散より小さくなる. 定積分の例では, もし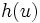 が単調な関数ならば,
が単調な関数ならば, 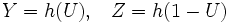 とするとよい.
とするとよい.
[共通乱数法]
二つの特性値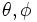 をそれぞれ確率変数
をそれぞれ確率変数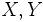 に関するモンテカルロ実験によって推定し, 比較したいものとし,
に関するモンテカルロ実験によって推定し, 比較したいものとし, ![\theta=E[X], \phi=E[Y] \,](https://cdn.weblio.jp/e7/img/dict/orjtn/fb13619d8a956585f893a1fbf3f8c1b4.png) とする.
とする.
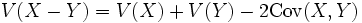
であるから, 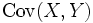 が大きいほど推定の精度が良くなる.
が大きいほど推定の精度が良くなる.  と
と の分布関数をそれぞれ
の分布関数をそれぞれ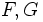 とし,
とし,  と
と を逆関数法で作るものとする. このとき,
を逆関数法で作るものとする. このとき,  と
と 用に別々の一様乱数列を使う代りに, ひとつの乱数列
用に別々の一様乱数列を使う代りに, ひとつの乱数列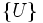 を使って,
を使って, 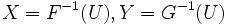 とすれば,
とすれば, 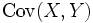 が最大となる. これが共通乱数法の原理である.
が最大となる. これが共通乱数法の原理である.
[1] 伏見正則, 『確率的方法とシミュレーション』(岩波講座 応用数学), 岩波書店, 1994.
[2] G. S. Fishman, Monte Carlo-Concepts, Algorithms, and Applications, Springer, 1996.
[3] A. M. Law and W. D. Kelton, Simulation Modeling and Analysis, 2nd. ed., McGraw-Hill, 1991.
| 非線形計画: | ベンダース分解法 ペナルティ関数法 ミニマックス定理 モンテカルロ法 ヤコビ行列 ラグランジュの双対性 ラグランジュ関数 |
| シミュレーション: | シミュレーテドアニーリング法 ペトリネット モデル モンテカルロ法 ランダム探索法 一様乱数 並列シミュレーション |
モンテカルロ法
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/06/10 06:36 UTC 版)
計算理論
計算理論の分野において、モンテカルロ法とは誤答する確率の上界が与えられる乱択アルゴリズム(ランダム・アルゴリズム)と定義される[1]。一例として素数判定問題におけるミラー-ラビン素数判定法がある。このアルゴリズムは与えられた数値が素数の場合は確実に Yes と答えるが、合成数の場合は非常に少ない確率ではあるが No と答えるべきところを Yes と答える場合がある。一般にモンテカルロ法は独立な乱択を用いて繰り返し、実行時間を犠牲にすれば誤答する確率をいくらでも小さくすることができる。またモンテカルロ法の中でも任意の入力に対して最大時間計算量の上界が入力サイズの多項式で与えられるものを効率的モンテカルロ法という[2]。
なお、これとは対照的に理論上必ずしも終了するとは限らないが、もし答えが得られれば必ず正しい乱択アルゴリズムをラスベガス法と呼ぶ。
計算複雑性理論では、確率的チューリング機械によるモデル化によってモンテカルロ法を用いて解決できる問題のクラスをいくつか定義している。代表的なところでは RPやBPP、PP などがある。これらのクラスと P や NP との関連性を解明していくことによって、モンテカルロ法のようにランダム性を含むアルゴリズムによって解ける問題の範囲が拡大しているのか(P ≠ BPP なのか)、それとも単に決定的アルゴリズムで解ける問題の多項式時間の次数を減らしているだけなのか(P=BPP なのか)は計算複雑性理論における主要課題の1つである。現在、NP ⊂ PP 、RP ⊆ NPであることはわかっているが BPP と NPとの関係はわかっていない。
準モンテカルロ法
一様乱数ではなく、超一様分布列を使用する方法を準モンテカルロ法という[3]。たとえばモンテカルロ数値積分法で、乱数の代わりに準乱数を用いれば収束の加速が期待できる。ただし、分布の一様性の高い数列としての準乱数は、モンテカルロ数値積分には適切であっても、それ以外の用途に用いた場合には、本来の答えと異なる結果を生じる可能性がある。
以下は超一様分布列の例である。
数値積分

数値解析の分野においてはモンテカルロ法はよく確率を近似的に求める手法として使われる。n 回シミュレーションを行い、ある事象が m 回起これば、その事象の起こる確率は当然ながら m/n で近似される。試行回数が少なければ近似は荒く、試行回数が多ければよい近似となる。
また、この確率を利用すれば、積分(面積)の近似解を求めることが可能となる。領域 R の面積 S は、領域 R を含む面積 T の領域内でランダムに点を打ち、領域 R の中に入る確率 p をモンテカルロ法で求めれば、S = pT で近似される。
n 重積分
- P.J. Davis and P.Rabinowitz、森正武(訳):「計算機による数値積分法」、日本コンピュータ協会(1981年2月15日)。
- Motwani, Rajeev; Raghavan, Prabhakar (1995). Randomized algorithms. Cambridge University Press. ISBN 0-521-47465-5. MR 1344451. Zbl 0849.68039
- Jan van Leeuwen 編:「コンピュータ基礎理論ハンドブックⅠ:アルゴリズムと複雑さ」、廣瀬 健、野崎昭弘、小林孝次郎 監訳、丸善、1994年、ISBN 4-621-03921-0
- 電気学会 GA・ニューロを用いた学習法とその応用調査専門委員会 編:『学習とそのアルゴリズム』、森北出版、2002年、ISBN 4-627-82751-2
- 杉原正顕、室田一雄:「数値計算法の数理」、岩波書店 2003年、ISBN 978-4-00-005518-5
- 伏見正則 、逆瀬川浩孝(監訳):「モンテカルロ法ハンドブック」、朝倉出版、ISBN 978-4-254-28005-0(2014年8月25日)。原著はDirk P.Kroese, Thomas Taimre, Zdravko I.Botev:Handbook of Monte Carlo Methods, John Wiley & Sons, Inc.,ISBN 978-0-47017793-8(2011年1月28日)。
- 鈴木航介、合田隆「準モンテカルロ法の最前線」『日本応用数理学会論文誌』第30巻第4号、日本応用数理学会、2020年、320-374頁、doi:10.11540/jsiamt.30.4_320、 ISSN 2424-0982。
- Müller, Fabio; Christiansen, Henrik; Schnabel, Stefan; Janke, Wolfhard (2023-07). “Fast, Hierarchical, and Adaptive Algorithm for Metropolis Monte Carlo Simulations of Long-Range Interacting Systems”. Phys. Rev. X (American Physical Society) 13 (3): 031006. doi:10.1103/PhysRevX.13.031006.
- K.K. Sabelfeld: Monte Carlo Methods: In Boundary Value Problems, Springer-Verlag, ISBN 978-3-642-75979-6 (1991).
- 鈴木航介、合田隆:「重点解説 モンテカルロ法と準モンテカルロ法」、サイエンス社(SGC 197)、ISBN 978-4-7819-1623-1 (2025年1月25日)。
関連項目
モンテカルロ法
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/12/10 02:35 UTC 版)
「モンテカルロ木探索」の記事における「モンテカルロ法」の解説
他のアプローチでは解決不可能または困難な決定問題をランダム性を使用するモンテカルロ法で解決する試みは、1940年代に始まった。ブルース・アブラムソンは、1987年の博士論文で、通常の静的評価関数ではなく、ミニマックス法をランダムなゲームプレイアウトに基づく期待結果モデルと組み合わせた。アブラムソンは、期待結果モデルは「正確・高精度で簡単に推定でき、効率的に計算でき、ドメインに依存しないことが示された」と述べた。アブラムソンは、三目並べ、リバーシ、チェスの機械生成の評価関数を詳細に実験した。 この方法は、1989年に、W・エルテル・シューマンとC・ズットナーによって、定理の自動証明の分野に適用され、幅優先探索、深さ優先探索、反復深化などの探索アルゴリズムにおいて、指数関数的な探索時間を改善することが発見された。 1992年、B・ブルークマンは、コンピュータ碁のプログラムに初めてそれを採用した。チャンらは、マルコフ決定プロセスモデルのアダプティブマルチステージサンプリング(AMS)アルゴリズムで「適応型」サンプリングを選択して、「再帰的ロールアウトとバックトラック」のアイデアを提案した。AMSは、サンプリング/シミュレーション(モンテカルロ)ツリーの構築におけるUCBベースの探査と開発のアイデアを探求した最初の試みであり、UCT(上位信頼性ツリー)のメインシードだった。
※この「モンテカルロ法」の解説は、「モンテカルロ木探索」の解説の一部です。
「モンテカルロ法」を含む「モンテカルロ木探索」の記事については、「モンテカルロ木探索」の概要を参照ください。
「モンテカルロ法」の例文・使い方・用例・文例
モンテカルロ法と同じ種類の言葉
「モンテカルロ法」に関係したコラム
-
モンテカルロ法は、勝率が33%、払い戻しが3倍の勝負に用いられる手法の1つです。1回目は「1、2、3」の数列を作り、両端の1と3の和の4をかけ金とします。ここで勝ったら次回も同じように「1、2、3」の...
- モンテカルロ法のページへのリンク





