モンテカルロ‐ほう〔‐ハフ〕【モンテカルロ法】
モンテカルロ法
モンテカルロ法
別名:モンテカルロ解析
【英】Monte Carlo method
モンテカルロ法とは、確率論的問題を解析するための手法で、大量の乱数を用いて何度もシミュレーションを行なうことによって近似解を求める計算手法のことである。
モンテカルロ法では、対象となる条件式に、コンピュータで発生させた乱数をあてはめる操作を繰り返すことによって様々な解のサンプルを大量に採取していく。解析的な手法によって解を得ることが困難な問題でも、膨大な量のシミュレーションを繰り返すことによって、解の値に接近してゆくことができる。
モンテカルロ法には、精度の高い近似解を得ようとすればするほど膨大な回数の計算が必要になるという困難があった。コンピュータによって多量の乱数を生成し、多量の演算を短時間で処理し、演算結果の統計まで行ってしまうことによって、非常に効率的な解析を可能とした。
モンテカルロ法は第二次大戦中、コンピューターの父と呼ばれるジョン・フォン・ノイマン(John Luis von Neumann)によって、中性子の物質中を動き回る様子を探るために考案されたといわれている。なお、当初から通称として呼ばれていたモンテカルロの名は、モナコ公国の首都モンテカルロにちなんだものであると言われている。
モンテカルロ法
モンテカルロ法 Monte Carlo Method
モンテカルロ法
【英】:Monte Carlo method
概要
乱数を使って実験する方法のこと. 第二次世界大戦中に原爆の開発に関する極秘プロジェクトを示す符丁として, フォンノイマン等がカジノで有名なモンテカルロに因んで命名したとされている.本来は, 確率的な変動を含まない問題を解くのに乱数を利用する方法のことであったが, 現在では乱数を使う実験の総称として使われることが多い.
詳説
システムの特性値などを推定するために, 適当なモデルと乱数を使って実験し, 大数の法則や中心極限定理などを利用して推測を行う方法のこと. システムに確率的な変動が内在する場合だけでなく, 確定的な問題を解くためにも使われる.
モンテカルロ法の原理を簡単な例で示そう. 推定したい特性値を 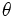 とし, これは既知の分布関数
とし, これは既知の分布関数  を持つ確率変数
を持つ確率変数  の関数
の関数 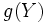 の平均値に等しいものとすれば,
の平均値に等しいものとすれば,
![\theta = E[g(Y)]=\int_{-\infty}^\infty g(y)\mathrm{d}F(y) =
\int_0^1 h(u) \mathrm{d}u, \,](https://cdn.weblio.jp/e7/img/dict/orjtn/b051904e001a6e946471c5f0d903dc80.png)
と書ける. ただし, 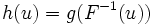 である. そこで, 区間[0,1]上の一様乱数
である. そこで, 区間[0,1]上の一様乱数 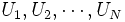 を発生し, 算術平均
を発生し, 算術平均
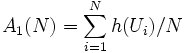
を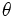 の推定値とすることが考えられる.
の推定値とすることが考えられる. 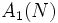 は
は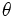 の不偏推定量であり, 分散は
の不偏推定量であり, 分散は
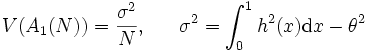
となる. したがって, 推定量 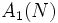 に含まれる誤差の標準偏差は
に含まれる誤差の標準偏差は 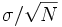 であり, 精度を十進で1桁上げるためには, サンプル数
であり, 精度を十進で1桁上げるためには, サンプル数  を10倍に増やさなければならない. このように, モンテカルロ法の収束は遅いので, これを改善するための方法が種々提案されており, 分散減少法と総称されている. ただし, これらは
を10倍に増やさなければならない. このように, モンテカルロ法の収束は遅いので, これを改善するための方法が種々提案されており, 分散減少法と総称されている. ただし, これらは 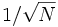 というオーダーを改善するものではなく, 比例係数を小さくするための工夫である.
というオーダーを改善するものではなく, 比例係数を小さくするための工夫である.
[重点サンプリング]
積分区間から一様にサンプルをとるのではなく, 重要と考えられる部分(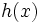 の絶対値が大きい部分)により多くの重みをおく密度関数
の絶対値が大きい部分)により多くの重みをおく密度関数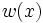 に従う乱数
に従う乱数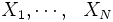 を発生し,
を発生し,
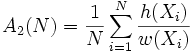
で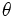 を推定する.
を推定する. 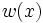 が
が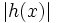 に比例するように選べれば分散は最小となるので, なるべくそれに近くなるように工夫する.
に比例するように選べれば分散は最小となるので, なるべくそれに近くなるように工夫する.
[制御変量法]
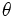 に対するひとつの不偏推定量を
に対するひとつの不偏推定量を とする.
とする.  と相関があって平均値
と相関があって平均値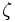 が既知の確率変数
が既知の確率変数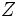 のことを,
のことを,  の制御変量という.
の制御変量という. 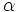 を定数として
を定数として
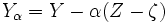
と定義すれば, 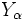 も
も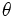 の不偏推定量となり, その分散は
の不偏推定量となり, その分散は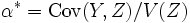 のとき最小となり, 最小値は
のとき最小となり, 最小値は
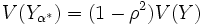
である. ここで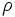 は
は と
と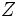 の相関係数であるから,
の相関係数であるから,  と相関の強い制御変量を選ぶほど効果的である.
と相関の強い制御変量を選ぶほど効果的である.
定積分の例では, 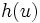 に近い関数
に近い関数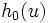 で, その積分の値
で, その積分の値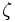 が正確に計算できるものを選び,
が正確に計算できるものを選び,
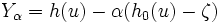
[負相関変量法]
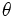 の不偏推定量
の不偏推定量 と平均値が同じで負の相関を持つ変量
と平均値が同じで負の相関を持つ変量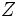 を利用して,
を利用して, 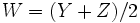 を
を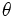 の推定量とする. この分散は,
の推定量とする. この分散は,  に対して2回独立にサンプルをとって平均する場合の分散より小さくなる. 定積分の例では, もし
に対して2回独立にサンプルをとって平均する場合の分散より小さくなる. 定積分の例では, もし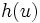 が単調な関数ならば,
が単調な関数ならば, 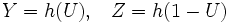 とするとよい.
とするとよい.
[共通乱数法]
二つの特性値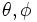 をそれぞれ確率変数
をそれぞれ確率変数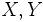 に関するモンテカルロ実験によって推定し, 比較したいものとし,
に関するモンテカルロ実験によって推定し, 比較したいものとし, ![\theta=E[X], \phi=E[Y] \,](https://cdn.weblio.jp/e7/img/dict/orjtn/fb13619d8a956585f893a1fbf3f8c1b4.png) とする.
とする.
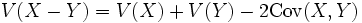
であるから, 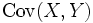 が大きいほど推定の精度が良くなる.
が大きいほど推定の精度が良くなる.  と
と の分布関数をそれぞれ
の分布関数をそれぞれ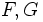 とし,
とし,  と
と を逆関数法で作るものとする. このとき,
を逆関数法で作るものとする. このとき,  と
と 用に別々の一様乱数列を使う代りに, ひとつの乱数列
用に別々の一様乱数列を使う代りに, ひとつの乱数列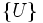 を使って,
を使って, 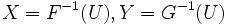 とすれば,
とすれば, 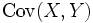 が最大となる. これが共通乱数法の原理である.
が最大となる. これが共通乱数法の原理である.
[1] 伏見正則, 『確率的方法とシミュレーション』(岩波講座 応用数学), 岩波書店, 1994.
[2] G. S. Fishman, Monte Carlo-Concepts, Algorithms, and Applications, Springer, 1996.
[3] A. M. Law and W. D. Kelton, Simulation Modeling and Analysis, 2nd. ed., McGraw-Hill, 1991.
| 非線形計画: | ベンダース分解法 ペナルティ関数法 ミニマックス定理 モンテカルロ法 ヤコビ行列 ラグランジュの双対性 ラグランジュ関数 |
| シミュレーション: | シミュレーテドアニーリング法 ペトリネット モデル モンテカルロ法 ランダム探索法 一様乱数 並列シミュレーション |
「Monte Carlo method」の例文・使い方・用例・文例
- Monte Carlo methodのページへのリンク



