ラグランジュ関数
ラグランジュ関数
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/07/13 08:32 UTC 版)
「ラグランジュ力学」の記事における「ラグランジュ関数」の解説
ラグランジュ関数(ラグランジアン、Lagrangian)は、物理的な力学系の動力学を記述するために用いられる関数である。ラグランジアン L ( q , q ˙ , t ) {\displaystyle L(q,{\dot {q}},t)} は一般に運動エネルギー T とポテンシャル V の差 L ( q , q ˙ , t ) = T − V {\displaystyle L(q,{\dot {q}},t)=T-V} の形で書かれる。 ラグランジアンはエネルギーの次元を持つスカラーであるが、観測可能な物理量ではなく、その値自体に物理的な意味があるわけではない。特に、座標と時間の任意関数 f ( q , t ) {\displaystyle f(q,t)} の時間による全微分を加える変換 L ′ ( q , q ˙ , t ) = L ( q , q ˙ , t ) + d d t f ( q , t ) {\displaystyle L'(q,{\dot {q}},t)=L(q,{\dot {q}},t)+{\frac {d}{dt}}f(q,t)} を行っても全く同じ力学系を表す。この全微分は連鎖律により d d t f ( q , t ) = q ˙ i ⋅ ∂ f ∂ q i + ∂ f ∂ t {\displaystyle {\frac {d}{dt}}f(q,t)={\dot {q}}_{i}\cdot {\frac {\partial f}{\partial q_{i}}}+{\frac {\partial f}{\partial t}}} となるので、この変換に対して、共役運動量は p i ′ = ∂ L ′ ∂ q ˙ i = p i + ∂ f ∂ q i {\displaystyle p'_{i}={\frac {\partial L'}{\partial {\dot {q}}_{i}}}=p_{i}+{\frac {\partial f}{\partial q_{i}}}} と変換される。したがって、新たな共役運動量の時間微分は p ˙ i ′ = p ˙ i + d d t ∂ f ∂ q i {\displaystyle {\dot {p}}'_{i}={\dot {p}}_{i}+{\frac {d}{dt}}{\frac {\partial f}{\partial q_{i}}}} となる。一方、一般化された力は ∂ L ′ ∂ q i = ∂ L ∂ q i + ∂ ∂ q i d d t f {\displaystyle {\frac {\partial L'}{\partial q_{i}}}={\frac {\partial L}{\partial q_{i}}}+{\frac {\partial }{\partial q_{i}}}{\frac {d}{dt}}f} と変換される。任意関数 f に作用する全微分 d/dt と座標の偏微分 ∂/∂q が交換可能なので、この変換に対して運動方程式が保たれる。
※この「ラグランジュ関数」の解説は、「ラグランジュ力学」の解説の一部です。
「ラグランジュ関数」を含む「ラグランジュ力学」の記事については、「ラグランジュ力学」の概要を参照ください。
- ラグランジュ関数のページへのリンク
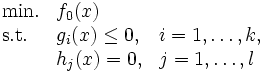
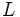 をラグランジュ関数という.
をラグランジュ関数という.
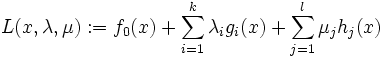
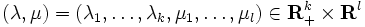 を
を