劣モジュラ最適化
【英】:submodular optimization
概要
劣モジュラ最適化とは, 劣モジュラ関数を制約条件または目的関数に含んだ離散最適化を指す. 劣モジュラ関数に関連した最適化問題に 対しては, 離散構造を利用した効率的なアルゴリズムが存在することが少なくない. そのため, 劣モジュラ最適化は, 非線形最適化における凸最適化のように, 離散最適化における基本的な位置を占めている.
詳説
劣モジュラ最適化 (submodular optimization) とは, 劣モジュラ関数 (submodular function) を制約条件または目的関数に含んだ離散最適化を指す. 劣モジュラ最適化は, 非線型最適化における凸最適化のように, 離散最適化における基本的な位置を占めている.
有限集合  の部分集合族
の部分集合族 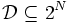 が,
が, 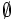 と
と  を共に含み, 任意の
を共に含み, 任意の 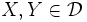 に対して
に対して 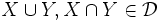 を満たすものとする. このとき,
を満たすものとする. このとき, 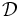 は分配束をなす. 関数
は分配束をなす. 関数  が, 任意の
が, 任意の 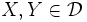 に対して
に対して
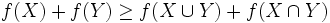
を満たすとき,  は劣モジュラ関数と呼ばれる. 不等号が常に等号で成立する場合には,
は劣モジュラ関数と呼ばれる. 不等号が常に等号で成立する場合には,  をモジュラ関数という. 分配束
をモジュラ関数という. 分配束 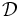 と劣モジュラ関数
と劣モジュラ関数  の組
の組 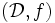 は,
は, 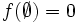 のとき, 劣モジュラシステム (submodular system) と呼ばれる. さらに,
のとき, 劣モジュラシステム (submodular system) と呼ばれる. さらに, 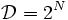 であり,
であり,  が単調性を有するとき, すなわち任意の
が単調性を有するとき, すなわち任意の 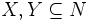 に対して
に対して 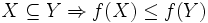 が成り立つとき,
が成り立つとき, 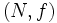 をポリマトロイド (polymatroid)という.
をポリマトロイド (polymatroid)という.
オペレーションズ・リサーチにおいて重要な劣モジュラ関数の代表的な例を以下に挙げる.
カット容量関数 有向グラフ 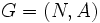 において, 各枝
において, 各枝 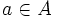 に非負の容量
に非負の容量  が与えられているとき,
が与えられているとき, 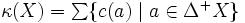 で定義される容量関数
で定義される容量関数 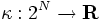 は, 劣モジュラ関数となる. ここで,
は, 劣モジュラ関数となる. ここで, 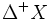 は,
は, 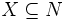 から出る枝の集合を表す.
から出る枝の集合を表す.
マトロイド階数関数 マトロイド 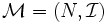 において, 階数関数
において, 階数関数 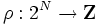 を
を 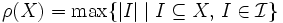 で定めると,
で定めると, 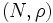 はポリマトロイドとなる.
はポリマトロイドとなる.
エントロピー関数 有限アルファベットの離散確率変数の集合  に関して, 空でない部分集合
に関して, 空でない部分集合 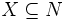 のエントロピーを
のエントロピーを 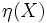 と書き,
と書き, 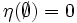 と定めると,
と定めると, 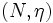 はポリマトロイドとなる.
はポリマトロイドとなる.
有限集合  上の実数値関数全体のなす線型空間を
上の実数値関数全体のなす線型空間を 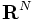 と表す. ベクトル
と表す. ベクトル 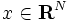 は, 部分集合
は, 部分集合 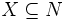 に対して
に対して 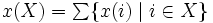 と定義することによって,
と定義することによって, 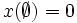 であるようなモジュラ関数
であるようなモジュラ関数  と同一視される.劣モジュラシステム
と同一視される.劣モジュラシステム 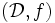 は,
は, 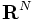 中の基多面体 (base polyhedron)
中の基多面体 (base polyhedron)
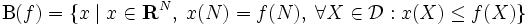
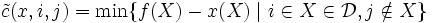
基多面体上では, 貪欲アルゴリズムによって, 線型目的関数の最適化が可能である. 一般に, 楕円体法を通じて, 最適化問題と分離問題とが計算量の多項式性という観点からは等価であるという原理に基づいて, 強多項式時間で劣モジュラ関数の最小化が可能であることが示されている [3] . しかし, 楕円体法は実際上効率的とは言い難く, 組合せ的な多項式時間アルゴリズムの開発が望まれていた. 2000年前後に, Iwata-Fleischer-Fujishige[6]とSchrijver[7]によって独立に解決された.
有向グラフ 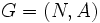 と,
と, 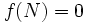 を満たす
を満たす  上の劣モジュラシステム
上の劣モジュラシステム 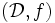 を考える. 各枝
を考える. 各枝 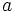 の始点を
の始点を 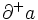 , 終点を
, 終点を 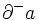 と書き,
と書き, 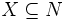 から出る枝の集合を
から出る枝の集合を 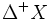 , 入る枝の集合を
, 入る枝の集合を  と表す. 任意の
と表す. 任意の 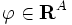 に対して, 境界
に対して, 境界 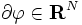 を
を 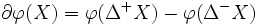 で定める. 劣モジュラフロー問題 (submodular flow problem) とは, 枝流量の上下限
で定める. 劣モジュラフロー問題 (submodular flow problem) とは, 枝流量の上下限 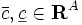 と費用
と費用 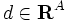 が与えられたとき,
が与えられたとき,
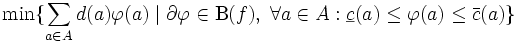
を求める問題である [1] . 特に,  がモジュラ関数の場合には, 最小費用フロー問題となることに注意する.
がモジュラ関数の場合には, 最小費用フロー問題となることに注意する.
劣モジュラフロー問題は, 任意の 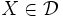 に対して
に対して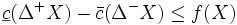 が成立するとき, かつそのときに限り, 実行可能解を有する. さらに,
が成立するとき, かつそのときに限り, 実行可能解を有する. さらに, 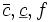 が整数値関数であれば, 整数実行可能解が存在する.
が整数値関数であれば, 整数実行可能解が存在する.
実行可能解 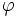 は, 以下の条件を満たす
は, 以下の条件を満たす 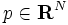 が存在するとき, かつそのときに限り, 最適解である. ただし, 各枝
が存在するとき, かつそのときに限り, 最適解である. ただし, 各枝 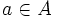 に対して
に対して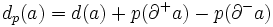 と定める.
と定める.
さらに,  が整数値関数の場合には,
が整数値関数の場合には,  を整数値関数に限ることができる.
を整数値関数に限ることができる.
最小費用フロー問題の解法を一般化することによって, 劣モジュラフロー問題を解くアルゴリズムが提案されている [5] . これらの組合せ的なアルゴリズムは, いずれも劣モジュラシステム 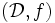 に関する交換容量を計算する手続きの存在を仮定している. 交換容量の計算は, 定義より明らかなように, 劣モジュラ関数の最小化になっており, 楕円体法を用いれば強多項式時間で可能なことが知られている. しかし, 劣モジュラフロー問題の応用に際しては, 問題の特殊性を活かした組合せ的な手続きが設計できる場合が少なくない.
に関する交換容量を計算する手続きの存在を仮定している. 交換容量の計算は, 定義より明らかなように, 劣モジュラ関数の最小化になっており, 楕円体法を用いれば強多項式時間で可能なことが知られている. しかし, 劣モジュラフロー問題の応用に際しては, 問題の特殊性を活かした組合せ的な手続きが設計できる場合が少なくない.
劣モジュラ関数  の最小値を達成する
の最小値を達成する 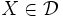 の全体は,
の全体は, 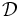 の部分分配束をなす. バーコフ(G. Birkhoff)の表現定理より, この部分分配束は
の部分分配束をなす. バーコフ(G. Birkhoff)の表現定理より, この部分分配束は  の適当な部分集合への分割と各成分間の半順序関係によって表すことができる. この原理に基づいて劣モジュラ関数で記述された離散システムを分解する手法を総称して基本分割 (principal partition) と呼ぶ.
の適当な部分集合への分割と各成分間の半順序関係によって表すことができる. この原理に基づいて劣モジュラ関数で記述された離散システムを分解する手法を総称して基本分割 (principal partition) と呼ぶ.
[1] J. Edmonds and R. Giles, "A min-max relation for submodular functions on graphs," in Studies in Integer Programming, P. L. Hammer, E. L. Johnson, and B. H. Korte, eds., North-Holland, 185-204, 1977.
[2] S. Fujishige, Submodular Functions and Optimization, 2nd ed., Elsevier, 2005.
[3] M. Grötschel, L. Lov\'asz and A. Schrijver, Geometric Algorithms and Combinatorial Optimization, Springer-Verlag, 1988.
[4] 伊理正夫, 藤重悟, 大山逹雄, 『グラフ・ネットワーク・マトロイド』, 産業図書, 1986.
[5] 岩田覚, 「劣モジュラ流問題」, 藤重悟 編 『離散構造とアルゴリズム Ⅵ』, 近代科学社, 第4章,127-170, 1999.
[6] S.Iwata, L.Fleischer and S.Fujishige, A combinatorial strongly polynomial algorithm for minimizing submodular functions, Journal of ACM 48 (2001) , 761--777.
[7] A.Schrijver, A combinatorial algorithm minimizing submodular functions in strongly polynomial time, Journal of Combinatorial Theory, Ser. B, 80 (2000) , 346--355.
| グラフ・ネットワーク: | 割当問題 劣モジュラシステム 劣モジュラフロー問題 劣モジュラ最適化 劣モジュラ関数 同形性 基多面体 |
劣モジュラ最適化と同じ種類の言葉
- 劣モジュラ最適化のページへのリンク
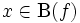 と
と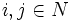
 , および
, および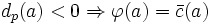 .
.
 .
.
