劣勾配
劣微分
(劣勾配 から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/05/13 05:40 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2022年8月)
|

数学において劣微分(れつびぶん、英: subderivative, subdifferential)とは一般の微分の概念を微分不可能な関数に対して拡張した考え方である。一般の関数の微分は関数であるが、劣微分の値は集合となる[1]。劣微分は凸解析の分野で広く用いられており、凸最適化と深い関係を持つ。
ある開区間 I 上の必ずしも全ての点で微分可能でない凸関数 f: I→R を考える。例えば絶対値を返す関数 f(x) = |x| などは x = 0 では微分不可能である。しかしながら右の図に示す通り、微分不可能な点を通り、その近傍の点とは接するか、あるいは下を通るような直線の集合を考えることができる.この直線それぞれの傾きの集合が劣微分の値となる。もし関数が下に凸ではなく上に凸である場合にも劣微分の定義は適用可能であるが、それはあまり重要な意味を持たないため、多くの場合、凸関数に対してのみ劣微分が定義される.
定義
凸関数 f: I→R の点 x0 における劣微分は次の条件を満たす数 c の集合である[1]。
-

この項目は、解析学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています(プロジェクト:数学/Portal:数学)。
- 劣勾配のページへのリンク
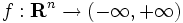
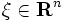 を
を  の
の  における劣勾配といい, 劣勾配
における劣勾配といい, 劣勾配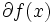 と表す.
と表す.
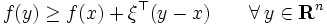
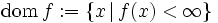 の
の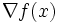 に
に