制約付き最適化
【英】:constrained optimization
概要
制約付き最適化とは, ベクトル空間上の連続関数を適当な(連続)集合上で最適化する問題およびその解法である. 代表的な制約付き最適化問題には線形計画問題, 2次計画問題, 多面体上の凸(非線形)関数最適化問題, 凸計画問題などがあり, 問題に応じた解法が考案されている. 一般的な問題にも適用できる解法としては, 逐次2次計画法や内点法がある.
詳説
制約付き最適化とは,  次元ベクトル空間上の連続関数
次元ベクトル空間上の連続関数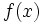 を適当な(連続)集合上で最適化する問題で一般に次の形で記述される.
を適当な(連続)集合上で最適化する問題で一般に次の形で記述される.
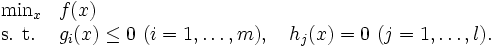
|
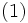 |
代表的な制約付き最適化問題には (A) 線形計画問題 (linear programming); (B) 2次計画問題 (quadratic programming); (C) 多面体上の凸(非線形)計画問題; (D) 凸計画問題 (convex programming); (E) (一般の) 非線形計画問題 (nonlinear programming)(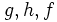 が一般の非線形関数である場合);があり, 各問題の特徴を生かした解法が研究されている.以下では主として(E)の解法について述べる.
が一般の非線形関数である場合);があり, 各問題の特徴を生かした解法が研究されている.以下では主として(E)の解法について述べる.
問題(1)に対するラグランジュ関数 (Lagrangian function)を次のように定義する.
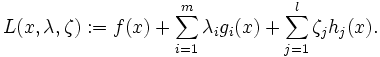 |
解法は, 最適性の必要条件であるカルーシュ・キューン・タッカー条件 (Karush-Kuhn-Tucker condition)
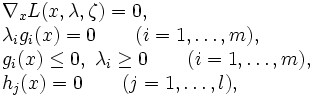
|
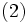 |
を満たす点(KKT点)を求めることを目的として設計される.探索方向を定め,その方向に適当なステップ幅だけ進むことを繰り返して漸近的にKKT点に収束する点列を生成する. 主な解法としては, (1) 射影勾配法 (gradient projection method)および有効制約法 (active set method); (2) ペナルティ関数法 (penalty function method); (3) 乗数法 (multiplier method); (4) 逐次2次計画法 (sequential quadratic programming method); (5) 内点法 (interior point method)が知られている. これらの内で実用性が高いとされるのは逐次2次計画法と内点法であるが, 制約領域が多面体である場合は有効制約法も用いられる.現状では, 逐次2次計画法により数百変数程度の中規模問題が, さらに内点法によって数千, 数万変数の大規模問題がある程度解けるようになりつつある.
勾配射影法は, 実行可能領域 (やその境界) の接平面の集合上に目的関数の勾配を射影してその(逆)方向に進む方法で、等式制約のみの問題に対するものが基本形である [2].有効制約法は制約領域が多面体である場合に対する勾配射影法の拡張である [2].
ペナルティ関数法は, 問題を無制約最適化問題に変換して解く方法であり,60年代に研究された[2, 4].この方法では, 目的関数に制約を満たさないことに対するペナルティ項を付加したペナルティ関数 (penalty function) を導入する. ペナルティ項が十分大きければ, ペナルティ関数を最小化することによって問題が近似的に解けるわけである. 典型的なペナルティ関数の一つは
![F_\rho^{\rm P}(x) := f(x) + \rho_1 \max_i[0, g_i(x)]^2 + \rho_2 \|h(x)\|^2](https://cdn.weblio.jp/e7/img/dict/orjtn/d4aff59024c09151c7e479d5d450d76b.png)
| 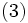 |
である. 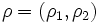 は正のパラメータでこれをペナルティパラメータと呼ぶ. 実際には, 大きな
は正のパラメータでこれをペナルティパラメータと呼ぶ. 実際には, 大きな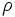 の値に対して
の値に対して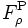 をいきなり最適化するのではなく,
をいきなり最適化するのではなく, 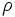 の値を徐々に大きくしながら
の値を徐々に大きくしながら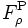 を無制約最適化するというステップを繰り返して問題を解く.
を無制約最適化するというステップを繰り返して問題を解く.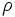 が大きくなるにつれて
が大きくなるにつれて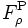 が悪条件になり無制約最適化が難しくなることが欠点とされる. 類似の方法で不等式制約を必ず満たすようにペナルティ項を付加したものは, 障壁関数法 (barrier function method)と呼ばれる.
が悪条件になり無制約最適化が難しくなることが欠点とされる. 類似の方法で不等式制約を必ず満たすようにペナルティ項を付加したものは, 障壁関数法 (barrier function method)と呼ばれる.
上に述べたペナルティ法の欠点を克服するために考えられたのが乗数法である [1, 3]. 乗数法は, 基本的には等式制約のみの問題を扱うための解法であり,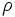 の他にラグランジュ乗数(Lagrangian multiplier)
の他にラグランジュ乗数(Lagrangian multiplier)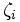 を導入して次のように定義される拡張ラグランジュ関数 (augumented Lagrangian function)
を導入して次のように定義される拡張ラグランジュ関数 (augumented Lagrangian function)
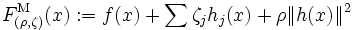
|
の無制約最適化を行って問題を解くものである.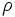 が十分大きく
が十分大きく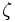 が元の問題のKKT点におけるラグランジュ乗数である時には, KKT点は
が元の問題のKKT点におけるラグランジュ乗数である時には, KKT点は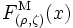 の極小点になる. そこで,
の極小点になる. そこで,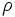 を十分に大きくとった上で, (i)適当な方法で
を十分に大きくとった上で, (i)適当な方法で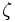 を推定し, (ii)
を推定し, (ii)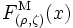 を無制約最適化する; という2つのステップを繰り返すことで,
を無制約最適化する; という2つのステップを繰り返すことで, 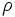 を更新することなくKKT点に収束する解法が得られる. 不等式制約
を更新することなくKKT点に収束する解法が得られる. 不等式制約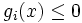 を持つ問題に対しては, スラック変数
を持つ問題に対しては, スラック変数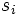 を導入して
を導入して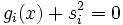 として, 等式制約に直した上でこの方法を適用すればよい. 乗数法は70年代に研究された.
として, 等式制約に直した上でこの方法を適用すればよい. 乗数法は70年代に研究された.
次に70年代後半から80年代に入って研究されたのが,逐次2次計画法である [2, 4, 6].逐次2次計画法では, 点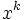 において, ラグランジュ関数
において, ラグランジュ関数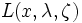 を2次近似し, 制約条件を1次近似して得られる2次計画問題
を2次近似し, 制約条件を1次近似して得られる2次計画問題
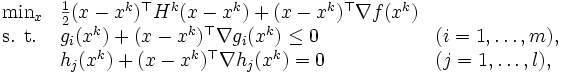
|
を解いてその方向に進んで次の点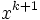 を定める. ここで
を定める. ここで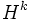 は
は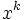 における
における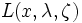 の変数
の変数 に関するヘッセ行列
に関するヘッセ行列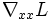 あるいはその近似行列である.
あるいはその近似行列である.
1984年のカーマーカー法(Karmarkar method)の登場以来, 内点法はさまざまな制約付き最適化問題に拡張された[5, 7]. 内点法には主内点法 (primal interior point method)と主双対内点法 (primal-dual interiorpoint method)の2種類がある.主内点法は, 基本的には不等式制約条件のみの最適化問題を取り扱う方法で,不等式制約を厳密に満たす点から出発して対数障壁関数 (log barrier function) ![\textstyle F_\nu^{\rm B}(x) := f(x) - \nu \sum_i \log[ - g_i(x)]](https://cdn.weblio.jp/e7/img/dict/orjtn/69549b490a0496b2a991d3c912502570.png) を逐次最小化して問題を解くものである.各
を逐次最小化して問題を解くものである.各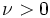 に対して
に対して を最小化する点が作る集合を中心曲線(central trajectory)という.
を最小化する点が作る集合を中心曲線(central trajectory)という.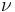 を小さくしながら
を小さくしながら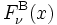 をニュートン法 によって最小化して中心曲線を追跡して問題を解く. 対数障壁関数は各不等式制約を定数倍する変換に対して不変であるという自然な性質を持つ.
をニュートン法 によって最小化して中心曲線を追跡して問題を解く. 対数障壁関数は各不等式制約を定数倍する変換に対して不変であるという自然な性質を持つ.
現在主流となりつつある主双対内点法は, 線形計画問題に対するものを拡張した次のような方法である[7]. この方法では新たに正のパラメータ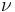 を導入し,カルーシュ・キューン・タッカー条件(2)の内,
を導入し,カルーシュ・キューン・タッカー条件(2)の内, 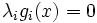 と
と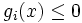 を,
を,
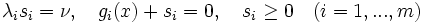 |
で置き換え, この条件を満たす点の集合を中心曲線とする. 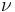 を小さくしながらニュートン法で中心曲線上の点を求めることを繰り返してKKT点に収束する点列を生成する.主双対内点法では,ラグランジュ乗数
を小さくしながらニュートン法で中心曲線上の点を求めることを繰り返してKKT点に収束する点列を生成する.主双対内点法では,ラグランジュ乗数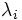 を導入することでペナルティ関数などの欠点であったKKT点の近くでの悪条件を克服している.
を導入することでペナルティ関数などの欠点であったKKT点の近くでの悪条件を克服している.
上述の各解法においてはKKT点や中心曲線上の点への近さを適当なメリット関数(merit function)で測り,各反復ではそれを減少させるようにステップ幅を選ぶ. メリット関数は探索方向の生成法と並んで解法の設計上重要な要素である. 無制約最小化することで元の制約付き最適化問題のKKT点が得られるような関数を厳密ペナルティ関数(exact penalty function)という. ペナルティ関数(3)で項![\rho_1\max[0, g_i(x)]^2\,](https://cdn.weblio.jp/e7/img/dict/orjtn/c9bf39c2bc5ae3dd87226bbe55bb98d1.png) ,
, 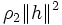 をそれぞれ
をそれぞれ![\rho_1\max[0, g_i(x)],\rho_2\|h\|_1](https://cdn.weblio.jp/e7/img/dict/orjtn/a9aa985e18430919f323afe3565b6c95.png) で置き換えたものは
で置き換えたものは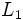 厳密ペナルティ関数と呼ばれ, 乗数法や逐次2次計画法に対するメリット関数としてよく用いられる.
厳密ペナルティ関数と呼ばれ, 乗数法や逐次2次計画法に対するメリット関数としてよく用いられる.
なお, 非線形関数の勾配やヘッセ行列の効率的な計算には高速自動微分法が有効であり,ヘッセ行列の近似行列を逐次構成する方法としては準ニュートン法がある. また, 線形計画問題に対する多項式内点法の理論は凸計画問題に拡張されている[5].
[1] D. P. Bertsekas: Nonlinear Programming, Athena Scientific, 1997.
[2] R. Fletcher: Practical Methods of Optimization, John Wiley, 1987.
[3] 藤田宏, 今野浩, 田邊國士:『最適化法』, 岩波書店, 1994.
[4] 福島雅夫:『数理計画入門』, 朝倉書店, 1996.
[5] Y. Nesterov and A. Nemirovskii: Interior Point Polynomial Algorithms in Convex Programming, SIAM, 1994.
[6] J. Nocedal and S. Wright: Numerical Optimization, Springer, 1999.
制約付き最適化と同じ種類の言葉
- 制約付き最適化のページへのリンク
