しゃ‐えい【射影】
射影
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/03/17 06:41 UTC 版)
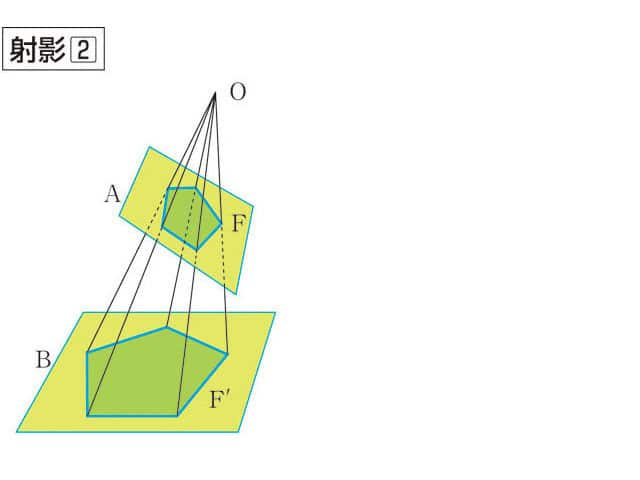
射影（しゃえい、projection）とは、物体に光を当ててその影を映すこと、またその影のことである。
- 集合論
- 直積集合の成分への標準射影 →射影 (集合論)
- 商集合への標準射影 →商写像
- 関係データベース
- 射影 → 対象となる列を抽出する操作
- 選択 → 対象となる行を抽出する操作
- 結合 → 複数の表を共通の列をキーとして連結し、別の表を作る操作
- 圏論
- 圏論的直積の成分への標準射影 →積 (圏論)
- 対象のある種の分類を与えるエピ射 →商対象
- 線型代数学
- 内積空間における（正）射影→射影作用素
- 位相幾何学
- 束の射影→ファイバー束、ベクトル束等を参照
- 関係代数の射影演算
- 関係代数 (関係モデル)#射影
関連項目
このページは曖昧さ回避のためのページです。一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。お探しの用語に一番近い記事を選んで下さい。このページへリンクしているページを見つけたら、リンクを適切な項目に張り替えて下さい。
射影
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/02/27 00:04 UTC 版)
「関係代数 (関係モデル)」の記事における「射影」の解説
射影（projection）演算は、ある関係から属性を限定した関係を返す。射影演算は、Rを構成する属性集合から、いくつかの属性を抽出する。βを抽出する属性の集合とすると、射影は、πβ(R) もしくは R[β] と記述することができる。
※この「射影」の解説は、「関係代数 (関係モデル)」の解説の一部です。
「射影」を含む「関係代数 (関係モデル)」の記事については、「関係代数 (関係モデル)」の概要を参照ください。
ウィキペディア小見出し辞書の「射影」の項目はプログラムで機械的に意味や本文を生成しているため、不適切な項目が含まれていることもあります。ご了承くださいませ。
お問い合わせ。
「射影」の例文・使い方・用例・文例
射影と同じ種類の言葉
品詞の分類
- >> 「射影」を含む用語の索引
- 射影のページへのリンク
