ニュートン法

OR事典

ニュートン法

読み方：にゅーとんほう
【英】：Newton's method

制約なし最適化問題 min 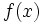(ただし 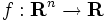)を解くための勾配法の1つである. 連立1次方程式 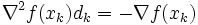の解 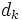を探索方向に選び, によって近似解の点列 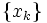を生成する. この解法は, 解の十分近くから出発すれば2次収束する.

「OR事典」の他の用語

非線形計画：

カルーシュ・キューン・タッカー条件  カーマーカー法  ダンツィク・ウルフ分解法  ニュートン法  フェンシェルの双対性  ヘッセ行列  ベンダース分解法

ウィキペディア

ニュートン法

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/02/13 08:11 UTC 版)

数値解析の分野において、ニュートン法（ニュートンほう、英: Newton's method）またはニュートン・ラフソン法（英: Newton–Raphson method）は、方程式系を数値計算によって解くための反復法による求根アルゴリズムの1つである。対象とする方程式系に対する条件は、領域における微分可能性と2次微分に関する符号だけであり、線型性などは特に要求しない。収束の速さも2次収束なので古くから数値計算で使用されていた。名称はアイザック・ニュートンとジョゼフ・ラフソンに由来する。ニュートン法を複素平面に適用し、初期値がどの解に収束するかについて色分けした結果としてニュートン・フラクタルを描くことができる（初期値の境界における挙動の予測が難しいことを示している）。

導入

ニュートン法の一手順の概念図 (青い線が関数 f のグラフで、その接線を赤で示した). x_n よりも x_n+1 のほうが、 f(x)=0 の解 x についてのよりよい近似を与えている.

この方法の考え方は以下のようである：まず初めに、予想される真の解に近いと思われる値をひとつとる。次に、そこでグラフの接線を考え、その x 切片を計算する。このx切片の値は、予想される真の解により近いものとなるのが一般である。以後、この値に対してそこでグラフの接線を考え、同じ操作を繰り返していく。

上の考え方は次のように定式化される。 ここでは、考える問題を f: R → R, x ∈ Rとして

$f(x)=0\,$

例として、 ${\sqrt {2}}$

ウィキメディア・コモンズには、ニュートン法に関連するカテゴリがあります。

• 除算 (デジタル)
• ガウス・ニュートン法
• ニュートン＝カントロビッチの定理

外部リンク

• 『ニュートン法の解説とそれを背景とする入試問題』 - 高校数学の美しい物語
• 山本哲朗、「Newton法とその周辺」『数学』 1985年 37巻 1号 p.1-15, doi:10.11429/sugaku1947.37.1, 日本数学会

ウィキペディア小見出し辞書

ニュートン法

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/11/01 02:18 UTC 版)

「求根アルゴリズム」の記事における「ニュートン法」の解説

初期値が根から遠い場合には必ずしも収束しないが、収束する場合は二分法より速い方法である。ニュートン法は、収束は通常2次であり、精度は1ステップ毎に2倍になる。関数 f が連続な微分値を持つことを前提とする。ニュートン法は、多次元の問題に直ちに一般化できる点でも重要である。より高次の収束を示す方法はハウスホルダー法に分類される。このうち最も単純なハレー法は3次の収束を示す。