ヘッセ行列
| 非線形計画: | ダンツィク・ウルフ分解法 ニュートン法 フェンシェルの双対性 ヘッセ行列 ベンダース分解法 ペナルティ関数法 ミニマックス定理 |
ヘッセ行列
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/07/02 15:19 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。(2015年10月)
|
数学におけるヘッセ行列(ヘッセ-ぎょうれつ、英: Hessian matrix)は、多変数スカラー値関数の二階偏導関数全体が作る正方行列である。実数値関数の極値判定に用いられる。ヘッセ行列は、ジェームス・ジョセフ・シルベスターが、ドイツの数学者ルートヴィヒ・オットー・ヘッセに由来して名づけた。
定義
実数値関数 f(x1, x2, ..., xn) に全ての二階偏微分が存在するとき、変数 xi に関する偏微分作用素を ∇i = ∂/∂xi とおくと、f のヘッセ行列 H(f) は、(i, j)-成分 H(f)ij が各点 x = (x1, x2, ..., xn) において
| 一般 |
|
|---|---|
| 微分可能 |
|
| 凸縮小化 |
|
||||
|---|---|---|---|---|---|
| 線型 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
ヘッセ行列
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/04/02 02:00 UTC 版)
詳細は「ヘッセ行列」を参照 二次導函数は、二次偏導函数の概念として高次元へ一般化される。函数 f: R3 → R に対して、これらは3つの二次偏導函数 ∂ 2 f ∂ x 2 , ∂ 2 f ∂ y 2 , ∂ 2 f ∂ z 2 {\displaystyle {\frac {\partial ^{2}f}{\partial x^{2}}},\;{\frac {\partial ^{2}f}{\partial y^{2}}},{\frac {\partial ^{2}f}{\partial z^{2}}}} および混合導函数 ∂ 2 f ∂ x ∂ y , ∂ 2 f ∂ x ∂ z , ∂ 2 f ∂ y ∂ z {\displaystyle {\frac {\partial ^{2}f}{\partial x\,\partial y}},\;{\frac {\partial ^{2}f}{\partial x\,\partial z}},{\frac {\partial ^{2}f}{\partial y\,\partial z}}} を含む。 函数の像と定義域の両方がポテンシャルを持つ場合、これらはヘッセ行列と呼ばれる対称行列に当てはまる。この行列の固有値は、二次導函数判定の多変量アナログを実装するために使用できる。(Second partial derivative test を参照せよ。)
※この「ヘッセ行列」の解説は、「二階導関数」の解説の一部です。
「ヘッセ行列」を含む「二階導関数」の記事については、「二階導関数」の概要を参照ください。
ヘッセ行列と同じ種類の言葉
- ヘッセ行列のページへのリンク
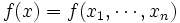 を各
を各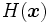 と
と![H(\boldsymbol x) :=
\left[
\begin{array}{ccc}
\frac{\partial^2 f}{\partial x_1\partial x_1}(\boldsymbol x)&\cdots&\frac{\partial^2 f}{\partial x_1\partial x_n}(\boldsymbol x)\\
\vdots & & \vdots\\
\frac{\partial^2 f}{\partial x_n\partial x_1}(\boldsymbol x)&\cdots&\frac{\partial^2 f}{\partial x_n\partial x_n}(\boldsymbol x)
\end{array}
\right].](https://cdn.weblio.jp/e7/img/dict/orjtn/489621b1de3e91cf4131e7ae18b76326.png)


