制約充足問題
【英】:constraint satisfaction problem
概要
与えられたすべての制約を満たすような各変数への値の割当てを求める問題.多くの組合せ問題を定式化することができ,問題解決の一般的な枠組みと位置付けられる.主に人工知能の分野で, 基盤技術の1つとして研究されている.
詳説
制約充足問題 (constraint satisfaction problem, CSP) は,一般に,  個の変数
個の変数 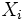
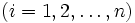 と各変数
と各変数 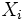 がとり得る有限個の値から成る領域
がとり得る有限個の値から成る領域 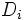 ,及び
,及び  個の制約
個の制約
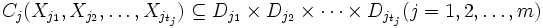
で定義される.制約 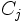 は,変数
は,変数 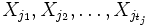 に対する
に対する 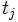 項制約であり,これらの変数が同時にとることのできる値の組の集合である.ここで, すべての制約を満たす値の組
項制約であり,これらの変数が同時にとることのできる値の組の集合である.ここで, すべての制約を満たす値の組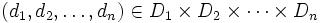 をCSPの解と呼び, (存在するならば) 一つ, あるいはすべての解を求めることがCSPの目的である.
をCSPの解と呼び, (存在するならば) 一つ, あるいはすべての解を求めることがCSPの目的である.
なお, 人為的に新たな変数を加えることで,多項制約を複数の二項制約で記述することができ,制約を二項制約に限定した形で定式化することも多く, 二項CSP (binary CSP) と呼ばれる.また, 上の定義では, 制約は値の組の集合で与えられるが, それらすべてを陽に記述する必要はなく,等式や論理式などを用いて表現することもできる.
CSPの高い定式化能力を活かして汎用問題解決器 (general problem solver) の開発が可能である.すなわち, 与えられた問題をCSPとして定式化し, その解を求めることで元の問題を解くことができる.この考えは制約プログラミングに通ずるものである. 制約プログラミングでは, 制約充足はシステムが行うものとし, それゆえ, 制約を記述することのみがプログラマ (ユーザ) の仕事であり, それ自体がプログラミングと考えられる [1].
CSPの解法としては,バックトラッキング法 (backtracking method) が代表的である. これは制約違反が起こらないように, ある順序に従って, 変数への値の割当てを順次行っていく方法であり, 木探索 (tree search) とも呼ばれる.変数に値を割当てる際, すべての制約を満たす値が存在しなければ, 一つ前の変数に戻ってその値を取消し, 他の値を試みる (バックトラック) という操作を繰り返す. この方法により, CSPを厳密に解くことが可能であるが, バックトラックが頻繁に発生する場合には効率的ではない. そこで, 木探索を効率的に行うための手法が種々提案されている. フォワードチェッキング (forward checking) は, 変数に値を割当てる度に, まだ値が割当てられていない変数の値域から, 制約に矛盾する値を予め削除しておく方法である. このとき, ある変数の値域が空になれば, 木探索を進めることなく, 現在の割当てが解の一部とはなり得ないと結論づけられる. このように, 制約に矛盾する値を変数の値域から削除する方法は, 一般に制約伝播 (constraint propagation) と呼ばれ, 問題縮小のための前処理としても用いられる. また, バックジャンピング (backjumping) では, 木探索において変数に値を割当てる際, そのすべての値が, 変数  以前に値が割当てられた変数と制約矛盾を起こす場合, 一つ前の変数に戻るのではなく, 変数
以前に値が割当てられた変数と制約矛盾を起こす場合, 一つ前の変数に戻るのではなく, 変数  まで戻ってその値を変更する. いずれも無駄な探索を防ぐために枝刈りを行うものであり, この他, バックマーキング (backmarking) やバックチェッキング (backchecking) などの手法が提案されている. また, バックトラックの数は, 値を割当てる変数の順序や変数に割当てる値の順序に依存する. これらの順序を発見的手法を用いて定める方法も提案されている [3].
まで戻ってその値を変更する. いずれも無駄な探索を防ぐために枝刈りを行うものであり, この他, バックマーキング (backmarking) やバックチェッキング (backchecking) などの手法が提案されている. また, バックトラックの数は, 値を割当てる変数の順序や変数に割当てる値の順序に依存する. これらの順序を発見的手法を用いて定める方法も提案されている [3].
上述の手法を用いることにより, 多少の探索の効率化が可能であるが, CSPが解を持つかどうかを決定する問題はNP完全であり, 多項式時間でCSPを(厳密に)解くアルゴリズムは存在しないと考えられる. そこで, バックトラックなしの木探索で(すなわち多項式時間で)解を一つ求めることができるCSPの部分クラスが, -整合 (
-整合 ( -consistency) や
-consistency) や  -木 (
-木 ( -tree) といった概念を用いて定義されている [2, 3].
-tree) といった概念を用いて定義されている [2, 3].
CSPに対する近似アルゴリズムの研究も数多くなされている.その多くは,すべての制約を満たすとは限らない全変数の値の組 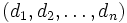 に対して, 値の変更を繰り返していくことで解を求めようとするものであり, 反復改善法 (iterative improvement) や山登り法 (hill climbing method) などと呼ばれている.厳密性は保証されないが, 実用上, 非常に有効であることが計算実験により確かめられている. これらの最も初期のものとしては, MCHC法 (min-conflict hill climbing) が挙げられる. これは,制約に違反している変数を一つ任意に選び, その値を制約違反数が最も少なくなる値に変更するという操作を, どの変数の値を変更しても制約違反数を減らすことができなくなるまで繰り返すものである. もちろんこれだけでは高い性能は望めず, 初期割当てを変えて何度か試行を繰り返すなどの工夫が必要である. ニューラルネットワーク (neural network) による近似解法の研究も比較的古く, 代表的なものとして GENET と呼ばれるものがある. その他多数の手法が提案されており, アニーリング法 (simulated annealing) や遺伝アルゴリズム (genetic algorithm) など, 組合せ最適化問題に対する一般的な枠組みとして近年盛んに研究されている, メタ戦略 (meta-heuristics) の適用も行われている [3].
に対して, 値の変更を繰り返していくことで解を求めようとするものであり, 反復改善法 (iterative improvement) や山登り法 (hill climbing method) などと呼ばれている.厳密性は保証されないが, 実用上, 非常に有効であることが計算実験により確かめられている. これらの最も初期のものとしては, MCHC法 (min-conflict hill climbing) が挙げられる. これは,制約に違反している変数を一つ任意に選び, その値を制約違反数が最も少なくなる値に変更するという操作を, どの変数の値を変更しても制約違反数を減らすことができなくなるまで繰り返すものである. もちろんこれだけでは高い性能は望めず, 初期割当てを変えて何度か試行を繰り返すなどの工夫が必要である. ニューラルネットワーク (neural network) による近似解法の研究も比較的古く, 代表的なものとして GENET と呼ばれるものがある. その他多数の手法が提案されており, アニーリング法 (simulated annealing) や遺伝アルゴリズム (genetic algorithm) など, 組合せ最適化問題に対する一般的な枠組みとして近年盛んに研究されている, メタ戦略 (meta-heuristics) の適用も行われている [3].
制約充足最適化問題 (constraint satisfaction optimization problem, CSOP) は, 解  に対してその評価値を定める関数
に対してその評価値を定める関数 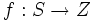 が与えられ, それを最小化(あるいは最大化)する問題である(ここで,
が与えられ, それを最小化(あるいは最大化)する問題である(ここで,  は解集合,
は解集合, 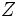 は整数集合). CSOPはCSPの拡張であり, スケジューリング問題など多くの現実問題を含む. CSOPの厳密解法としては, 分枝限定法が一般的である. 基本的には CSP のバックトラッキング法と同じであり, 無駄な探索を省くため, いかに効率良く枝刈りを行うかが重要となる.
は整数集合). CSOPはCSPの拡張であり, スケジューリング問題など多くの現実問題を含む. CSOPの厳密解法としては, 分枝限定法が一般的である. 基本的には CSP のバックトラッキング法と同じであり, 無駄な探索を省くため, いかに効率良く枝刈りを行うかが重要となる.
[1] 渕一博 監修, 溝口文雄, 古川康一, J-L. Lassez 編, 『制約論理プログラミング』, 1989.
[2] 西原清一, 「制約充足問題の基礎と展望」, 『人工知能学会誌』, 12 (3) (1997), 351-358.
[3] E. Tsang, Foundations of Constraint Satisfaction, Academic Press, 1993.
制約充足問題
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/10/01 00:24 UTC 版)
制約充足問題(せいやくじゅうそくもんだい、英: Constraint satisfaction problem, CSP)は、複数の制約条件を満たすオブジェクトや状態を見つけるという数学の問題を指す。CSPは特に人工知能やオペレーションズ・リサーチで研究されている。多くのCSPでは、それなりの時間内に解くのにヒューリスティクスと組合せ最適化手法を組み合わせる必要がある。
制約充足問題の具体例:
制約充足問題を解くアルゴリズムとしては、AC-3アルゴリズム、バックトラッキング、制約違反最小化などがある。
参考文献
- Tsang, Edward (1993年). Foundations of Constraint Satisfaction. Academic Press. ISBN 0-12-701610-4
- Dechter, Rina (2003年). Constraint processing. Morgan Kaufmann. ISBN 1-55860-890-7
- Apt, Krzysztof (2003年). Principles of constraint programming. Cambridge University Press. ISBN 0-521-82583-0
関連項目
外部リンク
- 制約充足問題のページへのリンク
