ラフ集合
【英】:rough set
概要
同値関係 による
による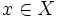 の同値類を
の同値類を
![[x]_R](https://cdn.weblio.jp/e7/img/dict/orjtn/757c20b296fcb1e3f88b0eb24b86abb4.png) と表すと,
集合
と表すと,
集合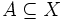 に対して,
上近似
に対して,
上近似![R^*(A) = \{ x \mid [x]_R \cap A \neq \emptyset\}](https://cdn.weblio.jp/e7/img/dict/orjtn/60207f006dfac4043ad9f5b11e462736.png) と
下近似
と
下近似![R_*(A) = \{ x \mid [x]_R \subseteq A \}](https://cdn.weblio.jp/e7/img/dict/orjtn/d1299ac53a2d49ee72a01603f37209d4.png) が得られる.
対
が得られる.
対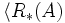 ,
,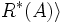 を
集合
を
集合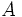 の
の -ラフ集合と呼ぶ.
ラフ集合は,識別不能性による曖昧さをモデル化しており,
類別や近似に深く関係している.
決定や診断における不要な属性の発見,
属性間の依存性の発見など,独特な方法が提案され,
近似識別や機械学習,意思決定に応用されている.
-ラフ集合と呼ぶ.
ラフ集合は,識別不能性による曖昧さをモデル化しており,
類別や近似に深く関係している.
決定や診断における不要な属性の発見,
属性間の依存性の発見など,独特な方法が提案され,
近似識別や機械学習,意思決定に応用されている.
詳説
ラフ集合は, 識別不能性(indiscernibility)による不確実性を扱う集合概念で, 1982年にポーランドの数学者 Zdzislaw Pawlak 教授により提案された[1,2]. いま, 全体集合として多くの対象の集合を考えよう. これらの対象を同等とみなせるグループ(同値類)に分割したとき, 任意の部分集合は, それに含まれるグループの和集合と, それと共通部分をもつグループの和集合により近似することができる. 前者は下近似と呼ばれ, 与えられた部分集合に確実に含まれる要素から構成される. 一方, 後者は上近似と呼ばれ, 与えられた部分集合に含まれるかもしれない要素からなる. 下近似と上近似とのペアをラフ集合という. 下近似と上近似は, それぞれ, 位相における集合の内部(interior)と閉包(closure), あるいは, 様相論理(modal logic)における必然性(necessity)と可能性(possibility)に対応している.
ラフ集合は, 決定表 (decision table)で与えられるデータを解析する基礎を与える. 決定表において, すべての条件属性の値が等しい対象は同値類としてグループ化できる. 一方, 決定属性値が等しい対象は決定クラスとしてまとめられる. これらより, 各決定クラスに対して下近似と上近似が求められることになる. ある決定クラスの下近似に帰属する対象は, 与えられた条件属性により正しく分類できる対象とみなされる. このことから, 下近似を用いて, 重要な条件属性を縮約 (reduct)やコア (core)として見出したり, 決定規則を極小長さのif-thenルールとして見出す方法が提案されている. ある決定クラスの上近似はどのような条件属性値をもつ対象が帰属しうるかを示しており, 可能性ルールの抽出に用いられる. また, すべての決定クラスの上近似は, どのような条件属性値をもつ対象がどの決定クラスに帰属しえないかを示しているので, この意味での重要な条件属性を求めることも考えられている[3].
このように, ラフ集合による解析法は, (1)数値データより名義データの方が取り扱いやすい, (2)条件属性の重要性を評価できる, (3)簡潔なif-thenルールが求められる などの特徴をもっており, 機械学習(machine learning)や知識発見(knowledge discovery), 特徴抽出(feature selection)などに利用され, 人工知能, 医療情報学, 土木工学, 感性工学, 決定科学, 経営学に応用されている.
ラフ集合は分割すなわち同値関係のもとで定義されてきたが, 被覆や順序関係(order relation), 類似関係(similarity relation), さらに一般の2項関係のもとでも定義されている. 順序関係のもとでのラフ集合は, 支配関係に基づくラフ集合(dominance-based rough set)と呼ばれ, 「燃費が高ければ高いほど購買意欲が高くなる」などのように, 条件属性(condition attribute)の一部と決定属性(decision attribute)とがともに序数属性で, 単調関係にある場合の決定表の解析に用いられる[4]. また, 条件属性の一部が序数属性で決定属性と単調関係がない場合には, 被覆のもとでのラフ集合が適用可能となる. 決定表の一部の条件属性データが欠損している場合は, トレランス関係(tolerance relation)という特別な類似関係のもとでのラフ集合により解析することができる[5]. 類似関係とは反射性を満たす関係をいい, トレランス関係は反射性と対称性とを満たす関係をいう. 以上は、通常の2項関係のもとでの通常の集合に対するラフ集合であったが, ファジィ関係のもとでのファジィ集合に対するラフ集合であるファジィラフ集合(fuzzy rough set)も考えられている[6].
ラフ集合の一般化は, もとになる2項関係を一般化したものばかりではなく, 下近似に帰属するための条件を一般化したラフ集合も考えられている. 与えられた決定表に誤差が含まれる場合には, 下近似が極めて小さくなり, ラフ集合により有益な解析が行えない場合がある. これに対処するため, ある程度の誤差を許容する可変精度ラフ集合 (variable precision rough set)が提案されている[7]. また, 可変精度ラフ集合において許容する誤差を定めることが容易でないことから, 情報ゲインに基づいたベイジアンラフ集合 (Bayesian rough set) が考えられている[8]. これらはラフメンバシップ値 (rough membership value) を用いて定義される.
ラフ集合は, 分割, 被覆, 支配関係, 類似関係などにより定められる対象のグループに基づき定義される. このようなグループは全体集合内の粒(granule)と考えられ, これに基づく計算法は, グラニュラーコンピューティング (granular computing)と呼ばれる[9]. 人間の言葉もグラニュラーコンピューティングに近いと考えられ, 言葉による計算の基礎となりうる. ラフ集合はこのようなグラニュラーコンピューティングを実現する手法としても注目されている.
[1] Z. Pawlak, "Rough Sets," International Journal of Computer and Information Sciences, 11 (5) (1982), 341-356.
[2] Z. Pawlak, Rough Sets: Theoretical Aspects of Reasoning About Data, Kluwer Academic Publishers, Dordrecht, 1991.
[3] 乾口,「ラフ集合による情報の解析」,『システム/制御/情報』, 49 (5) (2005), 162-172.
[4] S. Greco, B. Matarazzo and R. Slowinski, "The Use of Rough Sets and Fuzzy Sets in MCDM", in: T. Gal, T. J. Stewart and T. Hanne (eds.) Multicriteria Decision Making: Advances in MCDM Models, Algorithms, Theory, and Applications, Kluwer Academic Publishers, Dordrecht, 1999, pp.14-1-14-59.
[5] M. Kryszkiewicz, "Rough Set Approach to Incomplete Information Systems," Information Sciences, 112 (1-4)(1998), 39-49.
[6] M. Inuiguchi, "Generalizations of Rough Sets: From Crisp to Fuzzy Cases," in: S. Tsumoto, R. S{\l}owi\'{n}ski, J. Komorowski, J. W. Grzymala-Busse (eds.) Rough Sets and Current Trends in Computing: 4th International Conference, Proceedings, LNAI 3066, Springer-Verlag, Berlin, 2004, pp.26-37.
[7] W. Ziarko, "Variable Precision Rough Set Model," Journal of Computer and System Sciences, 46 (1) (1993), 39-59.
[8] D. Slezak and W. Ziarko, "The Investigation of the Bayesian Rough Set Model," International Journal of Approximation Reasoning, 40 (1-2) (2005), 81-91
[9] L. A. Zadeh, "From Computing with Numbers to Computing with Words: From Manipulation of Measurements to Manipulation of Perceptions," IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, 45 (1) (1999), 105-119
| 近似・知能・感覚的手法: | メタヒューリスティクス ラフセット ラフメンバシップ値 ラフ集合 人工生命 人工知能 制約充足問題 |
ラフ集合
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/12/22 07:46 UTC 版)
ナビゲーションに移動 検索に移動ラフ集合(ラフしゅうごう、Rough sets)とは上近似集合と下近似集合からなる集合で、非数値の対象を粗く(ラフに)記述することができるものである。これを用いることによって、他のデータマイニング手法からは得られにくい、非数値であったり矛盾のあるようなデータからの知識獲得が可能である。Rough sets theory(ラフ集合理論)の頭文字をとって RST や、Rough sets approach(ラフ集合アプローチ)の頭文字をとって RSA とも呼ばれる。
応用として、対象集合をファジィ集合に拡張したファジィ-ラフ集合理論 (Fuzzy-Rough sets theory) というものがある。
歴史
ラフ集合と同じ種類の言葉
- ラフ集合のページへのリンク
