PIとは - 日本語表現辞典 Weblio辞書

三省堂大辞林

索引トップ用語の索引ランキング凡例

パイ［1］【pi・ Π ・ π 】

①

ギリシャ語アルファベットの第一六字。

②

〘数〙

㋐

円周率を表す記号（ π ）。

㋑

相乗積を表す記号（ Π ）。

Π，π（ピー，パイ）

〖pī〗

①

ギリシャ語のアルファベットの第 16 字。

②

（π）円周率を表す記号。

③

（Π）相乗積を表す記号。

>>『三省堂大辞林』の表記・記号についての解説を見る

実用日本語表現辞典

索引トップ用語の索引ランキング

PI

英語：principal investment

投資家から資金を募り収益に応じて配当する、他人資金を用いた投資とは違い自己資金または借入を用いて行われる投資を意味する語。一部の証券会社などにおいてはPIの名を冠した部署があり、その部署を指すこともある言葉である。

時事用語のABC

索引トップ用語の索引ランキング

PI（ぴーあい）

公共事業で道路やダム、橋などの建設を行う際の手法だ。行政だけが政策決定に携わるのではなく、地域住民も政策決定に参加する。これによって、国民と行政側の双方向性のコミュニケーションを目指する。

具体的には、建設の計画を策定する段階で、アンケートを用いて地域住民から意見を集める。

実際のところ、施設を最終的に利用するのは地域住民だ。そこで利用者である住民の視点をもっと政策決定に取り入れるべき、というのがＰＩの思想だ。

（2000.08.28更新）

大車林

索引トップ用語の索引ランキング画像一覧

PI

英語 polyimide

主鎖にイミド基結合をもつ耐熱性高分子の総称。

※「大車林」の内容は、発行日である2004年時点の情報となっております。

石油/天然ガス用語辞典

索引トップ用語の索引ランキング画像一覧

産出指数

読み方：さんしゅつしすう
【英】: productivity index
略語: PI

油井の原油産出能力（production capacity または well potential）を表す指数で、一般に PI と呼ばれる。PI は坑井の単位ドローダウン・プレッシャーあたりの原油生産レートを表現するもので、次式で定義される。
PI＝q_o /（P_ws－P_wf）［kL/d/（kg/cm²）］または［b/d/psi］
q_o：産出レート［kL/d］または［b/d］
P_ws：密閉坑底圧力［kg／cm²］または［psi］
P_wf ：流動坑底圧力［kg／cm²］または［psi］

このPI は常に一定の値ではなく、生産を続けていく過程で変化するが、PI の値が大きな坑井は生産性が良いといえる。油井の PI は、これが決定されるとドロー・ダウン・プレッシャーと生産レートの関係が分かるため、適正生産量を決めるうえで一つの指標となる。

スラグ用語集

索引トップ用語の索引ランキング

PI

別名：ぴーあい

土あるいは路盤材料中に含まれる細粒分等が塑性状態にある含水量の大きさをいい、液性限界と塑性限界の含水比の差で表される。この指数は土の分類に使われるほか、路盤材等の品質規格の判定項目にも使われている。ＩＰ＝ＷＬ－ＷＰここにＩＰ：塑性指数〔％〕ＷＬ：液性限界〔％〕ＷＰ：塑性限界〔％〕塑性指数は砂質土で０である。粘土分が多くなるに従がい大きくなる。

塑性指数

読み方：そせいしすう
別名：ぴーあい
【英】：PI,plasticity index

土あるいは路盤材料中に含まれる細粒分等が塑性状態にある含水量の大きさをいい、液性限界と塑性限界の含水比の差で表される。この指数は土の分類に使われるほか、路盤材等の品質規格の判定項目にも使われている。ＩＰ＝ＷＬ－ＷＰここにＩＰ：塑性指数〔％〕ＷＬ：液性限界〔％〕ＷＰ：塑性限界〔％〕塑性指数は砂質土で０である。粘土分が多くなるに従がい大きくなる。

針入度指数

読み方：しんにゅうどしすう
別名：ぴーあい
【英】：PI,penetration index

アスファルトの針入度と軟化点より求められるアスファルトの感温性を示す指数で一般にPIで表わし、次式より計算される。
PI＝30/(1+50A)?10ここで　A＝（log 800?log pen（25 ℃））/（軟化点（℃）　?25（℃））log pen（25 ℃）： 25 ℃における針入度の対数 log 800 ：軟化点における針入度を800とした対数針入度指数が大きいほど感温性が小さい。つまり高温で流動を起こしにくく、低温でクラックやはく離を起こしにくい傾向を示す。

日本化学物質辞書Web

索引トップランキング

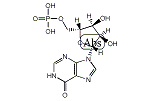
ＩＭＰ

分子式：	C₁₀H₁₃N₄O₈P
慣用名：	イノシン酸、ヒポキサンチンリボシド5-りん酸、pI、IMP、Ino-5'-P、Inosinic acid、5'-Inosinic acid、Hypoxanthine riboside-5-phosphoric acid、9-(5-O-Phosphono-β-D-ribofuranosyl)-9H-purin-6(1H)-one、Inosine 5'-phosphoric acid、5'-IMP、Inosine 5'-phosphate、2-Deamino-5'-guanylic acid、9-[5-O-(Dihydroxyphosphinyl)-β-D-ribofuranosyl]-1,6-dihydro-9H-purine-6-one
体系名：	9-(5-O-ホスホノ-β-D-リボフラノシル)-9H-プリン-6(1H)-オン、イノシン5'-りん酸、5'-イノシン酸、イノシン5'-ホスファート、2-デアミノ-5'-グアニル酸、9-[5-O-(ジヒドロキシホスフィニル)-β-D-リボフラノシル]-1,6-ジヒドロ-9H-プリン-6-オン

「日化辞Web」で詳細を見る

生物学用語辞典

索引トップ用語の索引ランキングカテゴリー

ホスファチジルイノシトール

英訳・(英)同義/類義語：phosphatidylinositol, PI , Phosphatidylinositol (PI), phosphatidylinositol

細胞膜を構成する酸性のリン脂質で、ジアシルグリセロールの3位OH基とイノシトールのOH基がリン酸ジエステルで結合した化合物。

エイズ関連用語集

索引トップ用語の索引ランキング

ＰＩ

PI, Protease Inhibitor

Protease Inhibitorの短縮形。『プロテアーゼ阻害剤』を参照。

《参照》プロテアーゼ阻害剤

外国人名読み方字典

索引トップ用語の索引ランキング

Pi

名前ピ；ピー；ピィ

ウィキペディア

索引トップ用語の索引ランキングカテゴリー

PI

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2013/06/06 11:06 UTC 版)

PI, pi, Pi, pI

ギリシア文字 π
- 円周率
イタリア共和国トスカーナ州ピサ県の県名略記号およびISO 3166-2:IT県名コード
パブリック・インボルブメント（Public Involvement）
パッケージ・インテグレーション（Package Integration）
XMLにおける処理命令（Processing Instructions）
パーリ語のISO 639-1言語コード
画像圧縮フォーマットの一つ。Pi (画像圧縮)を参照
PIアドレス（Provider Independent Address）。プロバイダ非依存のIPアドレス
パールインデックス。ある避妊法を一年間用いた場合に、避妊に失敗する確率（厳密な定義ではないが、妊娠する確率ともいえる）をパーセントで示したもの
プロフォーマ・インボイス（Proforma Invoice）
テレビ新潟放送網（TeNY）の識別信号（コールサイン）（JOPI-DTV）
ブラジル連邦共和国の州、ピアウイ州
Pi（ペビ）は2⁵⁰を表す接頭辞の単位。2進接頭辞を参照
無機リン酸のこと。Piと表記する
等電点（pI：isoelectric point）
PI（Principal investigator）。研究プロジェクト・研究グループの長のこと。一般に大学の教授、准教授

このページは曖昧さ回避のためのページです。一つの言葉や名前が二つ以上の意味や物に用いられている場合の水先案内のために、異なる用法を一覧にしてあります。お探しの用語に一番近い記事を選んで下さい。このページへリンクしているページを見つけたら、リンクを適切な項目に張り替えて下さい。

円周率

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2014/01/30 10:17 UTC 版)

(PI から転送)

円周率

定義
円周の長さを C、直径を d とすると、 π = C/d
使用
円板の面積（英語版） • 周長 • 他の数式での使用
特性
無理性 • 超越性
数値
22/7 より小さい • 近似（英語版） • 覚え方
人物
アルキメデス • 劉徽 • 祖沖之 • マーダヴァ • ウィリアム・ジョーンズ（英語版） • ジョン・マチン • ジョン・レンチ（英語版） • ルドルフ・ファン・コーレン • アリヤバータ
歴史
歴史 • 書籍
文化
法律 • 記念日
関連項目
円積問題 • バーゼル問題 • ファインマン・ポイント
表・話・編・歴

円周率（えんしゅうりつ）は、円の周長の直径に対する比率として定義される数学定数である。通常、ギリシア文字 π（パイ）で表される。数学をはじめ、物理学、工学といった様々な科学分野に出現し、最も重要な数学定数とも言われる。

円周率は無理数、つまりその小数展開は循環しない。小数点以下35桁までの値は次の通りである。

π = 3.14159 26535 89793 23846 26433 83279 50288 …

円周率は、無理数であるのみならず、超越数でもある。

基礎

表記と呼び方

π という文字は、周辺・地域・円周などを意味するギリシア語 περιφέρεια（ペリフェレイア）の頭文字である。ウィリアム・オートレッドやアイザック・バローにより円周を表す記号として用いられ、ウィリアム・ジョーンズやレオンハルト・オイラーなどにより円周の直径に対する比率を表す記号として用いられた。日本では「パイ」と発音する。

π は国によっては別名がある。例えばそれを計算した人物の名前を取った、「アルキメデス数」、「ルドルフ数」、日本においては「円周率」がそれに当たる。

なお、「π」の字体は、表示環境によってはキリル文字の п に近い π などと表示されることがある。なお、大文字の「パイ」 $\Pi$ は数列の総乗を表す記号である。

定義

幾何学的な定義

直径 1 の円の周長は π

平面幾何学において、円周率 π は、円の周長の直径に対する比率として定義される。円の周長を C、直径を d とすると、

$\pi =\frac{C}{d}$

全ての円は互いに相似なので、この比率は円の大きさに依らず一定である。

他の定義

上記の定義は、円の周長を用いているため、曲線の長さを最初に定義していない現代数学の分野では、π が現れる際に問題となることがある。この場合、円の周長に言及せず、解析学などにおける性質の一つを π の定義とすることが多い^[1]。この際の π の定義の一般なものとして、三角関数 cos x が 0 を取るような x > 0 の最小値の2倍とするもの、定積分による定義などがある。

歴史

「円周率の歴史」も参照

円に内接する正多角形による π の近似

円に内接・外接する正多角形による π の近似。アルキメデスによる計算。

古代

円周の直径に対する比率が円の大きさに依らず一定であり、それが 3 より少し大きい程度だということは古代エジプトやバビロニア、インド、ギリシアの幾何学者たちにはすでに知られていた。また、古代インドやギリシアの数学者たちの間では半径 r の円の面積が πr² であることも知られていた。さらに、アルキメデスは半径 r の球の体積が 4/3πr³ であることや、この球の表面積が 4πr²（その球の大円の面積の4倍）であることを示した。

2千年紀

14世紀インドの数学者・天文学者であるサンガマグラマのマーダヴァは次のような π の級数表示を見いだしている（ライプニッツの公式）：

$\frac{\pi}{4} =1-\frac{1}{3} +\frac{1}{5} -\frac{1}{7} +\cdots =\sum_{n=0}^{\infty} \frac{(-1)^n}{2n+1}$

これは逆正接関数 Arctan x のテイラー展開の x = 1 での実現になっている。マーダヴァはまた、

$\pi =\sqrt{12} \left( 1-\frac{1}{3\cdot 3} +\frac{1}{5\cdot 3^2} -\frac{1}{7\cdot 3^3} +\cdots \right)$

を用いて π の値を小数点以下11桁まで求めている。

18世紀フランスの数学者アブラーム・ド・モアブルは、コインを 2n 回投げたときに表が x 回出る確率は、n が十分大なら、ある定数 C を取ると、

$\frac{C}{\sqrt{n}} \exp \left\{ -\frac{(x-n)^2}{n} \right\}$

で近似できることを、n = 900 における数値計算により見いだした。この正規分布の概念は1738年に出版されたド・モアブルの『巡り合わせの理論』に現れている。ド・モアブルの友人のジェイムズ・スターリングは後に、 $C=\frac{1}{\sqrt{2\pi}}$ であることを示した。

1751年にヨハン・ハインリッヒ・ランベルトは、x が 0 でない有理数ならば正接関数 tan x の値は無理数であることを示し、その系として π は無理数であることを導いた。さらに1882年にフェルディナント・フォン・リンデマンは π が超越数であることを示し、円積問題（与えられた長さを半径とする円と等積の正方形を作図する問題）は解くことができないことを導いた。

コンピュータによる計算の時代

20世紀以降、コンピュータの発達により、計算された円周率の桁数は増大した。1949年に、ジョン・フォン・ノイマンはコンピュータ ENIAC を使い70時間かけて、円周率を2037桁まで計算した^[2]。その後の数十年間、さまざまな計算機科学者によって計算は進められ、1973年には100万桁を超えた。この進歩は高速なハードウェアの開発だけによるものではなく、効率のよいアルゴリズムが考案されたためである。そのうちの最も重要な発見の一つとして、1960年代の高速フーリエ変換がある。これにより、多倍精度の演算が高速に実行できるようになった。

2011年現在では、円周率は小数点以下10兆桁まで計算されている^[3]。

性質

無理性

π は無理数である。つまり、2つの整数の商で表すことはできず、小数展開は循環しない。このことは1761年にヨハン・ハインリッヒ・ランベルトが証明したが、厳密性に欠けた部分があった。その部分は1806年にルジャンドルによって補われた。

円周率は無理数であることの証明については「円周率の無理性の証明」を参照

したがって、円周率のコンピュータによる計算や暗唱、10進法における各数字 (0～9) の出現頻度は、興味の対象となる。

超越性

さらに、π は超越数である。つまり、有理数係数の有限次代数方程式の根とはならない。これは1882年にフェルディナント・フォン・リンデマンによって証明された（リンデマンの定理）。これより、整数から四則演算と冪根をとる操作だけを有限回組み合わせて π の正確な値を求めることはできないことが分かる。

円周率は超越数であることの証明については「リンデマンの定理」を参照

π が超越数であることより、古代ギリシアの三大作図問題の内の一つ「円積問題」（与えられた長さを半径とする円と等積の正方形を作図すること）が不可能であることが従う。

ランダム性

π は現在小数点以下10兆桁を超える桁まで計算されている。数字 0～9 がランダムに現れているようには見えるが、実際は、π が正規数であるかどうかは分かっていない。例えば π の10進表示において、各桁を順に取り出して得られる数列：

3, 1, 4, 1, 5, 9, 2, 6, 5, 3, 5, …（オンライン整数列大辞典の数列 A796）

には、0～9 が均等に現れるのかどうか、すなわち、この数列が乱数列になっているかどうかは分かっていない。それどころか、0～9 がそれぞれ無限に現れるのかどうかすら分かっていない。

したがって、10兆桁以降の桁についてもランダムであるかどうかは、現在分かっていないのである。

ベイリーとクランドールの2000年の発表によると、ベイリー＝ボールウィン＝プラウフの式を用いて2進表示で様々な桁の計算をした結果では、各数字の出現率はカオス理論に基づいていると推測できるようである。

5兆桁までの数字の出現回数は以下の通りである。全てほぼ等しく、最も多いのは 8、最も少ないのは 6 である。

0：4999億9897万6328回

1：4999億9996万6055回

2：5000億0070万5108回

3：5000億0015万1332回

4：5000億0026万8680回

5：4999億9949万4448回

6：4999億9893万6471回

7：5000億0000万4756回

8：5000億0121万8003回

9：5000億0027万8819回

未解決問題

$\pi \pm e, \pi e, \frac{\pi}{e}, \pi^\pi, \pi^e, \pi^\sqrt{2}, e^{{\pi}^2}$ は超越数か?
$\pi$ は正規数か?

この節の加筆が望まれています。

円周率に関する式

π についての式は非常に多い。ここではその一部を紹介する。数式によってはそれ自体が π の定義になり得るし、π の近似値の計算などにも使われてきた。

幾何

半径 r の円の周長：L(r) = 2πr
半径 r の円の面積：A(r) = πr²
半径 r の球の体積：V(r) = 4/3πr³
半径 r の球の表面積：S(r) = 4πr²
半軸が a と b の楕円の面積：A(a, b) = πab
180° = π ラジアン

解析

$\frac{2}{1} \cdot \frac{2}{3} \cdot \frac{4}{3} \cdot \frac{4}{5} \cdot \frac{6}{5} \cdot \frac{6}{7} \cdot \frac{8}{7} \cdot \frac{8}{9} \cdots =\frac{\pi}{2}$ （ウォリス）
$\zeta (2)=\frac{1}{1^2} +\frac{1}{2^2} +\frac{1}{3^2} +\frac{1}{4^2} +\cdots =\frac{\pi^2}{6}$ （1735年：オイラー、バーゼル問題、ゼータ関数）
$\zeta (4)=\frac{1}{1^4} +\frac{1}{2^4} +\frac{1}{3^4} +\frac{1}{4^4} +\cdots =\frac{\pi^4}{90}$
$\frac{\pi^2}{6} =\sum_{n=1}^\infty \frac{1}{{n^2}2^{n-1}} +(\log 2)^2$ （オイラー）
$\zeta (2n)=\frac{(-1)^{n-1} 2^{2n-1} B_{2n}}{(2n)!} \pi^{2n} \ (n\in \mathbb{N})$ （B_n はベルヌーイ数）
$\int_{-\infty}^\infty e^{-x^2} \, dx=\sqrt{\pi}$ （ガウス積分）
$\Gamma \left( \frac{1}{2} \right) =\sqrt{\pi}$ （ガンマ関数）
$n!\sim \sqrt{2\pi n} \left( \frac{n}{e} \right)^n$ （スターリングの近似。f(n)～g(n) は $\lim_{n\to\infty}\frac{f(n)}{g(n)}=1$ を表す）
$\sum_{k=1}^n \phi (k)\sim \frac{3n^2}{\pi^2}$ （φ(k) はオイラーのφ関数）
e^πi + 1 = 0（オイラーの等式）
$\frac{1}{\pi} =\frac{2\sqrt{2}}{99^2} \sum_{n=0}^\infty \frac{(4n)!(1103+26390n)}{(4^n99^nn!)^4}$ （ラマヌジャン）
$\frac{4}{\pi} =\sum_{n=0}^\infty \frac{(-1)^n(4n)!(1123+21460n)}{882^{2n+1}(4^nn!)^4}$ （ラマヌジャン）
$\sqrt{\frac{1}{2}} \sqrt{\frac{1}{2} +\frac{1}{2} \sqrt{\frac{1}{2}}} \sqrt{\frac{1}{2} +\frac{1}{2} \sqrt{\frac{1}{2} +\frac{1}{2} \sqrt{\frac{1}{2}}}} \cdots =\frac{2}{\pi}$
の連分数表示：
- $\frac{4}{\pi} =1+ \cfrac{1}{3+ \cfrac{4}{5+ \cfrac{9}{7+ \cfrac{16}{9+ \cfrac{25}{11+ \cfrac{36}{13+ \cfrac{49}{\ddots}}}}}}}$

数論

整数全体から無作為に2つ取り出す時、その2つが互いに素である確率は $\frac{6}{\pi^2}$ である。

証明については「互いに素#互いに素である確率」を参照

力学系・エルゴード理論

ロジスティック写像 x_i+1 = 4x_i(1 − x_i) により帰納的に定まる数列 {x_i} を考える。初期値 x₀ を 0 以上 1 以下に取るとき、そのほとんど全てで、次が成り立つ。

$\lim_{n \to \infty} \frac{1}{n} \sum_{i = 1}^n \sqrt{x_i} =\frac{2}{\pi}$

統計

$f(x)=\frac{1}{\sigma\sqrt{2\pi}} \, e^{-\frac{(x-\mu )^2}{2\sigma^2}}$ （正規分布の確率密度関数）
幅 1 の無数の平行線の上から長さ 1/2 の針を落とすとき、その針が直線と共有点を持つ確率は 1/π である（ビュフォンの針）。

その他

河川の長さの水源－河口間の直線距離に対する比率は、平均すると円周率に近い^[4]。

暗唱

語呂合わせ

π の桁を記憶術に頼らずに暗記する方法が各種存在している。

日本語では、語呂合わせにより、長い桁を暗記するのも比較的簡単である。有名なものとして、以下がある。

産	医	師	異	国	に	向	かう	産	後	厄	な	く	産	婦	み	や	し	ろ	に	虫	散	々	闇	に	鳴	く
3.	1	4	1	59	2	6	5	3	5	89	7	9	3	2	3	8	4	6	2	64	3	3	83	2	7	9	（30桁）

英語圏では語呂合わせがうまくいかないため、単語の文字数で覚える方法がある。

Yes,	I	have	a	number.
3.	1	4	1	6	（小数点以下4桁までで四捨五入）

How	I	want	a	drink,	alcoholic	of	course,	after	the	heavy	lectures	involving	quantum	mechanics!
3.	1	4	1	5	9	2	6	5	3	5	8	9	7	9	（14桁）

How	I	want	a	drink,	alcoholic	of	course,	after	the	heavy	lectures	involving	quantum	mechanics!	and	if	the	lectures	were	boring	or	tiring,	then	any	odd	thinking	was	on	quartic	equations	again
3.	1	4	1	5	9	2	6	5	3	5	8	9	7	9	3	2	3	8	4	6	2	6	4	3	3	8	3	2	7	9	5	（31桁）S.ボトムリー

これらのような覚え方は多くあり、日本語では上記のものの改編で90桁までのものや、歌に合わせたもの、数値を文字に置き換えて1,000桁近く覚える方法などがある。

暗唱記録

『ギネス世界記録』によれば、円周率暗唱の世界記録は2005年 11月20日に6万7890桁を暗唱した中国人、呂超（西北農林科技大学大学院生）が記録したものである^[5]^[6]。

2004年 9月25日、原口證が8時間45分かけて円周率5万4000桁の暗唱に成功し、従来の世界記録を更新した。しかしながら、実際はより多くの桁を覚えていたため、2005年 7月1日～7月2日に再挑戦し、8万3431桁までの暗唱に成功した。2006年 10月3日午前9時～10月4日午前1時30分（16時間30分）の挑戦で円周率10万桁の暗唱に成功した。ギネス世界記録に申請中である。

文化的影響

ベルリン工科大学数学科の近くにあるタイル

円という日常でもよく知られた図形についての単純な定義でありながら、小数部分が無限に続くという不思議さから、数学における概念の中で最もよく知られたものの一つである。

3月14日は円周率の日および数学の日である。また7月22日（22/7 は近似値）は円周率近似値の日とされている。
2012年 8月14日、米国勢調査局が、米国の人口が円周率と同じ並びの3億1415万9265人に達したと発表した。アメリカには円周率の曲を作る人もいる^[7]。

この節の加筆が望まれています。

参考文献

^ Rudin, Walter (1976) [1953]. Principles of Mathematical Analysis (3e ed.). McGraw-Hill. p. 183. ISBN 0-07-054235-X.
^ "An {ENIAC} Determination of pi and e to more than 2000 Decimal Places", Mathematical Tables and Other Aids to Computation, 4 (29), pp. 11–15. (January, 1950)
^ “長野男性、円周率で１０兆桁達成　自作パソコンで”. 共同通信. (2011年10月16日) 2011年10月17日閲覧。
^ サイモン・シン著、青木薫訳、『フェルマーの最終定理』、新潮社、2000年、ISBN 4-10-539301-4、42ページ
^ 陝西省の大学院生、円周率暗唱のギネス新記録樹立
^ レコードチャイナ：円周率6万桁以上を暗唱、世界記録に輝いた「記憶の達人」-陝西省楊凌市
^ 米国の人口が円周率と「同じ」に　３億１４１５万９２６５人 CNN 2012.08.15 Wed posted at 12:42 JST

Berggren, Lennart; Borwein, Jonathan and Borwein, Peter (1991). Pi: A Source Book. Springer-Verlag. ISBN 0-387-94924-0.
上野健爾　『円周率 π をめぐって』　日本評論社、1999年。ISBN 4-535-60840-7。
牧野貴樹　『円周率100,0000桁表』　暗黒通信団、1996年。ISBN 978-4-87310-002-9。

外部リンク

Weisstein, Eric W., "Pi" - MathWorld.（英語）
PlanetMath: Pi
Wolfram Alpha, Pi
円周率のはじめの百万桁
（参考）円周率.com - ドメイン（Webアドレス）が3.14から64ケタ目まであるサイト（英語）

	先負
	馬鮫魚
	赤口
	及第点
	注意喚起
	吝かではない
	汎用性
	日々精進
	共益費
	ご用命


	Copyright (C) 2001-2014 Sanseido Co.,Ltd. All rights reserved. 株式会社三省堂、三省堂 Web Dictionary
	Copyright © 2014 実用日本語表現辞典 All Rights Reserved.
	Copyright©2014 時事用語のABC All Rights Reserved.
	Copyright c San-eishobo Publishing Co.,Ltd.All Rights Reserved.
	Global Disclaimer（免責事項）本資料は石油天然ガス・金属鉱物資源機構（以下「機構」）石油・天然ガス調査グループが信頼できると判断した各種資料に基づいて作成されていますが、機構は本資料に含まれるデータおよび情報の正確性又は完全性を保証するものではありません。また、本資料は読者への一般的な情報提供を目的としたものであり、何らかの投資等に関する特定のアドバイスの提供を目的としたものではありません。したがって、機構は本資料に依拠して行われた投資等の結果については一切責任を負いません。なお、本資料の図表類等を引用等する場合には、機構資料からの引用である旨を明示してくださいますようお願い申し上げます。 ※Copyright (c) 2014 Japan Oil, Gas and Metals National Corporation. All Rights Reserved. このホームページに掲載されている記事・写真・図表などの無断転載を禁じます。
	Copyright (C) 2014 Nippon Slag Association All Rights Reserved.
	All Rights Reserved, Copyright © Japan Science and Technology Agency
	Copyright (C) 2014 NII,NIG,TUS. All Rights Reserved.
	Copyright (C) 2014, Chugoku-Shikoku Regional AIDS Center
	Copyright (C) 1994- Nichigai Associates, Inc., All rights reserved.
	All text is available under the terms of the GNU Free Documentation License. この記事は、ウィキペディアのPI (改訂履歴)、円周率 (改訂履歴)の記事を複製、再配布したものにあたり、GNU Free Documentation Licenseというライセンスの下で提供されています。 Weblio辞書に掲載されているウィキペディアの記事も、全てGNU Free Documentation Licenseの元に提供されております。

11	自己研鑽
12	繁忙期
13	偉大なる、しゅららぼん
14	KSD事件
15	豊原功補
16	外税・内税表示
17	Fワード
18	ご容赦ください
19	全聾
20	河原健二

21	ご指導ご鞭撻
22	今生の別れ
23	意思疎通
24	虎視眈々
25	語彙力
26	秋桜（コスモス）
27	他言無用
28	ご教示
29	万障お繰り合わせの上
30	セフレ

PIとは？

パイ ［1］ 【pi・ Π ・ π 】

Π，π（ピー，パイ）

PI

PI（ぴーあい）

PI

産出指数

PI

塑性指数

針入度指数

ＩＭＰ

ホスファチジルイノシトール

ＰＩ

Pi

PI

円周率

目次

基礎

表記と呼び方

定義

幾何学的な定義

他の定義

歴史

古代

2千年紀

コンピュータによる計算の時代

性質

無理性

超越性

ランダム性

未解決問題

円周率に関する式

幾何

解析

数論

力学系・エルゴード理論

統計

その他

暗唱

語呂合わせ

暗唱記録

文化的影響

参考文献

関連項目

外部リンク

関連ニュース

PIに関係した商品

「PI」の関連用語

画像から探す

パイ［1］【pi・ Π ・ π 】