論理プログラミング
【英】:logic programming
概要
知識や森羅万象の因果関係を論理記号と非論理記号を使って形式的に記述したものは論理式と呼ばれる. この中で一階述語論理式と呼ばれ, "それを成り立つようにするには, いくつかのそれぞれ異なる条件が満たされればよい" ことを記述する論理式集合の処理を対象として, ある論理式が成り立つかどうかの検証過程を計算過程とみなしたコンピュータプログラムを論理プログラム, このような計算原理に基づくプログラム法を論理プログラミングという.
詳説
論理とは「推理の仕方, 論証の筋道」を意味し, 論理学とは「正しい認識を得るための規範となるべき思惟の法則及び形式を研究する学問一般」をいう. その中で 記号論理学 (symbolic logic) とは「論理の対象となる思考の終局的要素とその基本的な関係を数学の記号に類するもので表現し, 論理的操作を数学の演算に類する操作で行う論理学」であって, 論理計算, 数学的論理学と大体同義であるとされる [1]. 従って, 記号論理は論理推論 (logical reasoning) 分野に属し, その研究はわれわれの興味の対象要素(思考の終局的要素)と対象間の論理的関係を操作し, 論証の道筋を検証し, 正しい認識を得ることに関する方法論の探究を意味する.
このことはわれわれが計算機を使って計算を行う, 問題を解く, あるいは, 対象を計算機で制御するなどの諸計算行為と多くの類似点をもつ. しかし, こうした (数値的) 計算行為には, 使用するプログラム言語のもつ諸規則 (文法など) や計算順序などを勘案しつつアルゴリズムを構築しプログラミングを行うことが要求されるため, こうした方法では, 知識としての論理の対象となる思考の終局的要素とその基本的な関係を, 直接表現し利用することは, 従来, 困難であった. 近年, 知識工学 (knowledge engineering) と呼称され, 知識を計算行為の対象, すなわち知識処理を対象とする分野が展開されてきた. これは知識を約束に従って記号化し, いわゆる知識ベースとして計算機の中にこれを蓄え, これらを利用しつつ, 対象問題 (ここでは命題) を解こうとする研究分野であって, 記号論理学がその理論的基礎を成す.
さて, 知識工学では, 理論・実用の両面にわたって特に多くの研究やシステム開発が, 一階述語論理(first-order predicate logic)を利用して行われている. 一階述語論理に基づく場合, 知識は記号列で表現され, 知識の操作は, 短い列から長い列を生成する構文的規則(syntax), 与えられた記号列を解釈する意味論的規則 (semantics), 構文的規則に基づく推論規則 (rule of inference) および系全体に関する公理 (axiom) に基づいて行われる. これは例えて言えば, アルファベットから単語が構成され, 単語群から文節が構成され文節群から文が構成される仕組である. 文法に相当するものとして構文的規則があり, 文字列としての単語や文節, 文章の意味解釈に相当する操作が意味論的規則に則って用意される.
記号論理的に見ると一階述語論理の記号列は, 論理記号 (結合子, 限定記号など) と非論理記号 (定数, 変数, 述語, 関数) からなり, 非論理記号に固有の意味を与えたとき, その解釈は一意的に決まる. このことを, 一階言語を定めたという. またここで言う述語 (predicate) は, その引き数である定数や変数の状態や性状 (つまり, ~である;~する, など) を記述する. 述語の解釈としての論理的意味付けには, ブール代数では0か1, 二値論理では真か偽, ファジィ論理では数値的真理値や言語的(linguistic)真理値を割り当てる. 変数や定数, さらに, 変数や定数をすべての引数に代入した関数を項 (term) と呼ぶ.  変数の述語の各引数に項を代入した論理式を原子論理式 (atomic formula) といい, これらを論理記号で結合したものも論理式という. さらに, 論理式同士を論理記号で結合したものも論理式という. 代表的論理式同士の関係を意味づけしたものがいわゆる真理値表 (truth table) を構成する.
変数の述語の各引数に項を代入した論理式を原子論理式 (atomic formula) といい, これらを論理記号で結合したものも論理式という. さらに, 論理式同士を論理記号で結合したものも論理式という. 代表的論理式同士の関係を意味づけしたものがいわゆる真理値表 (truth table) を構成する.
論理式 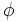 を真とするある解釈と項への値割り当てが存在するならば, この論理式は充足可能 (satisfiable) であるという. さらに論理式の集合
を真とするある解釈と項への値割り当てが存在するならば, この論理式は充足可能 (satisfiable) であるという. さらに論理式の集合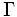 を充足する任意の解釈と割り当てがある論理式
を充足する任意の解釈と割り当てがある論理式 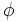 を充足するとき, この論理式
を充足するとき, この論理式 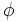 は論理式集合
は論理式集合 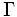 の論理的帰結と呼ばれる. ゲーデルの完全性定理 (completeness theorem) によれば, ある論理式
の論理的帰結と呼ばれる. ゲーデルの完全性定理 (completeness theorem) によれば, ある論理式 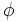 が論理式集合
が論理式集合 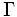 の論理的帰結であるならば, 論理式集合
の論理的帰結であるならば, 論理式集合 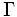 からその論理式
からその論理式 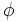 を導く有限の長さの記号列を生成できる. これは論理式集合から有限回のステップで機械的に論理的帰結を導くことができるアルゴリズムの存在を言明している. ここから一階述語論理の推論規則として唯一定義されるモーダス・ポーネスが提示される. すなわち, "二つの論理式
を導く有限の長さの記号列を生成できる. これは論理式集合から有限回のステップで機械的に論理的帰結を導くことができるアルゴリズムの存在を言明している. ここから一階述語論理の推論規則として唯一定義されるモーダス・ポーネスが提示される. すなわち, "二つの論理式 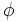 と
と 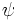 があり, 論理式
があり, 論理式 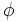 が論理式集合
が論理式集合 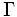 の論理的帰結かつ「
の論理的帰結かつ「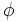 ならば
ならば 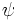 」も
」も 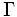 の論理的帰結ならば,
の論理的帰結ならば, 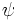 は
は 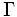 の論理的帰結である. "これは連続値を扱うファジィ推論 (fuzzyinference) [3] の場合にも前提, 条件および近似的帰結として成り立つ推論規則である.
の論理的帰結である. "これは連続値を扱うファジィ推論 (fuzzyinference) [3] の場合にも前提, 条件および近似的帰結として成り立つ推論規則である.
次に, 論理プログラミング (logic programming) において重要な「証明」の概念を述べる. 論理式の列 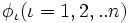 が存在し, 全ての
が存在し, 全ての 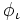 が公理か, 論理式集合
が公理か, 論理式集合 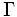 の元か, または列のそれ以前に位置する他の論理式からモーダ・ポーネスによって導かれたか, のいずれかが成り立つとする. この時, 論理式の列
の元か, または列のそれ以前に位置する他の論理式からモーダ・ポーネスによって導かれたか, のいずれかが成り立つとする. この時, 論理式の列 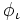 は論理式
は論理式 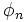 の証明と呼ばれ, 論理式
の証明と呼ばれ, 論理式 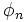 は論理式集合
は論理式集合 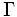 から証明可能である, といわれる.
から証明可能である, といわれる.
以上の議論の結果として形式的知識表現としての論理式はプログラムに, その推論過程としての証明は計算に対応することが理解できる. 現実的視点から一階述語論理のある制限されたクラスのみを対象としてプログラミング環境を実現したものを論理プログラミングという. そのような制限されたクラスとしてホーン節がある. 一般に論理プログラミングでは, 与えられた論理式の否定(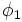 )からトップダウン的またはボトムアップ的に導出原理を利用して演繹的に空節(
)からトップダウン的またはボトムアップ的に導出原理を利用して演繹的に空節(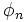 )を導くという証明の手続きが利用される. このようにして
)を導くという証明の手続きが利用される. このようにして 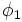 の充足不可能性を証明することによって, 元の論理式が真であることを証明するのである. 論理プログラミングにおける代表的プログラム言語がPROLOGであり, わが国の第5世代コンピュータ計画をはじめとして知識工学, 人工知能分野に多くの影響を与えている.
の充足不可能性を証明することによって, 元の論理式が真であることを証明するのである. 論理プログラミングにおける代表的プログラム言語がPROLOGであり, わが国の第5世代コンピュータ計画をはじめとして知識工学, 人工知能分野に多くの影響を与えている.
論理プログラミングの直接的応用としてはパズル, 定理証明などが知られているが, その実際的応用はいわゆる各種エキスパートシステム (expert system) の構築にある. エキスパートシステムでは, 事実や専門家の知識を論理式, 特にホーン節形式で表現して知識ベースとして蓄え, 知識ベースの内容を論理式集合 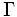 として, 与えられた問題 (論理式) に対して論理的帰結を自動的に得る手続きを論理プログラミングが受け持つ [4]. 論理プログラミングによる証明の解釈そのものが, エキスパートシステムにおいては人間への自動説明機能となる. このようなエキスパートシステムの持つ宿命的課題は必要十分な知識をいかに獲得するかである. 知識獲得 (knowledge acquisition) の方法として人手による方法ばかりではなく自律的学習機能を導入する研究もなされている. さらに, 実用上の問題として蓄えた知識の上の推論の非単調性 (non-monotonicity) の問題, すなわち新しく入力された知識が以前の知識と矛盾するような結果を引き起こす現象がしばしば起こることが指摘されている. これに対する有力な方法は未だに確立されていないが, 実際にはこのような場合でも非単調推論 (non-monotonic reasoning) と呼ばれる方法が利用される.
として, 与えられた問題 (論理式) に対して論理的帰結を自動的に得る手続きを論理プログラミングが受け持つ [4]. 論理プログラミングによる証明の解釈そのものが, エキスパートシステムにおいては人間への自動説明機能となる. このようなエキスパートシステムの持つ宿命的課題は必要十分な知識をいかに獲得するかである. 知識獲得 (knowledge acquisition) の方法として人手による方法ばかりではなく自律的学習機能を導入する研究もなされている. さらに, 実用上の問題として蓄えた知識の上の推論の非単調性 (non-monotonicity) の問題, すなわち新しく入力された知識が以前の知識と矛盾するような結果を引き起こす現象がしばしば起こることが指摘されている. これに対する有力な方法は未だに確立されていないが, 実際にはこのような場合でも非単調推論 (non-monotonic reasoning) と呼ばれる方法が利用される.
論理プログラミングが人の論理的知識を蓄積し利用しようとするものであるのに対して, 定性推論 (qualitative inference) は物理法則に基づいた因果関係を基本として, 対象とする系の動的挙動を定性的に推論し, 理解しようとする [5]. 通常は微分方程式で表わされ解析され理解されるところの物理現象を, 素朴に理解しようとするものと考えることができるが, 計算機の数値計算能力に依存する部分がある. 定性推論は物理現象に対して素直に抱く疑問「なぜ?」, 「こうなったらどうなる?」に答えるのに有効な推論方式と考えられる.
ここで取り上げた伝統的な記号論理的推論に基づく論理プログラミング, 曖昧さを導入したファジィ推論, あるいは知識の直接利用を狙ったエキスパートシステム, さらには, 物理現象の動的振る舞いを対象とする定性推論を有機的に結合することにより, 真に有効な人工知能が実現されることを期待したい.
[1] 新村出編, 『広辞苑(第5版)』, 岩波書店, 1998.
[2] 森下真一, 『知識と推論』, 情報数学講座10, 共立出版, 1997.
[3] 水本雅晴, 『ファジィ理論とその応用』, サイエンス社, 1988.
[4] 安部憲広, 滝寛和, 『エキスパート・システム入門』, 共立出版, 1987.
論理プログラミング
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/04/12 06:28 UTC 版)
| プログラミング・パラダイム |
|---|
|
論理プログラミング(Logic Programming)とは、数理論理学(記号論理学)を基礎にしたプログラミングパラダイム、または数理論理学のコンピュータプログラミングへの応用である。形式論理の論理式をソースコードの書式に投影することが基本になる。プログラミングに適用するための幅広い解釈が加えられており、研究対象としての論理プログラミングは非常に多様である。
より一般的に受け入れられている論理プログラミングは、述語論理を基礎にし、問題領域の事実と規則を論理式モデル書式で表現して(ロジック)非決定性の演繹の導出原理を用いる(コントロール)というものである。このアルゴリズムスタイルで最も普及した論理プログラミング言語は「Prolog」である。
概要
論理プログラミングの基本は数理論理学のスタイルをコンピュータのプログラミングに持ち込むことにある。数学者や哲学者は論理を理論構築のツールとして選んだ。多くの問題は理論として自然に表現される。解決すべき問題とは、新たな仮説が既存の理論で説明できるかどうかを問うことと等しい。論理は問題が真か偽かを証明する方法を提供する。証明構築過程は明確であり、論理は問題に答える信頼できる方法と見なされている。論理プログラミングシステムはこの過程を自動化する。人工知能は論理プログラミングの開発に重要な影響を与えた。
この観点での論理プログラミングは、ジョン・マッカーシー[1958]のadvice takerの提案にまでさかのぼることができる。より一般的に受け入られている狭い意味での論理プログラミングは、述語論理式を非決定的なプログラミング言語とみなすもので、述語論理式は宣言的であると同時に手続き的にも解釈される。
論理をベースにしたプログラミング言語として1971年に Planner のサブセットである Micro-Planner が開発された。表明とゴールからパターンによる手続き的計画を呼び出す機能を備えていたが、十分に形式化されていなかった[1]。Plannerと独立してより論理を重視した Prolog が開発され、コワルスキーにより述語論理式(ホーン節)のプログラム的解釈の考え方と結び付き、論理プログラミングの基本的な考え方が確立した[2]。Planner からの派生で、プログラミング言語 Poplerが開発された。Prolog からの派生言語としては、Mercury、Visual Prolog、Oz、Fril などがある。バックトラッキングを使用しない並行論理プログラミング言語としてProlog からの派生したConcurrent Prolog、PARLOG、GHC、KL1などの各種言語(Shapiro [1989] に調査結果がある)がある。
数理論理学適用の限界
ジョン・マッカーシーは数理論理学をコンピュータシステムの認識論の基礎として利用することを提案した。MITではマービン・ミンスキーとシーモア・パパートが主導して、マッカーシーとは異なる手続き的手法が開発された。Planner が開発されたとき、これら2つの手法の関係に関する疑問が生まれた。Robert Kowalski は「計算は推論に包含される」という命題を生み出した。彼はこれを 1988年の Pat Hayes の論文にあった言葉「計算は制御された推論である」が元になっているとしている。Kowalski や Hayes とは逆に、カール・ヒューイットは「論理的推論はオープンシステムの並行計算を実行することが不可能だ」という命題を生み出した。
論理的手法と手続き的手法の関係という問題の答えは、手続き的手法の数学的意味(表示的意味論)と論理の数学的意味(モデル理論)は異なる、ということである。
歴史
論理プログラミングは、1950年代から盛んになった自動定理証明と、1958年公開言語「LISP」を最初の実践手段にしている。マサチューセッツ工科大学でLISPを開発したジョン・マッカーシーは、Advice takerという常識推論仮説を発表している。
適切な形式言語(述語論理計算の一部に近い)を処理するプログラムは共通の”声明書”になる。基本プログラムは前提から直ちに結論を導き出す。その結論は宣言的かもしれないし命令的かもしれない。命令的結論が導出されたら、プログラムはそれに応じた動作もする。
ジョン・マッカーシーは更にこう補足しており、これは最初の人工知能仮説のようである。
我々がadvice takerに期待する主な利点は、その記号環境と探求物についての”声明”を作成するだけで、その動作が改良されるということである。”声明”の作成には、プログラム知識やadvice takerの事前知識をほとんど要求されないだろう。advice takerは事前知識に基づく広範囲な論理的帰結を取り揃えられると仮定できる。従って次のように言える。『事前知識を豊富に与えられ、自動演繹を行うプログラムは常識を備えている』
なお、マッカーシーは現代で言われる論理プログラミングの形態にはそれほど関与していない。
宣言的知識表現と手続き的知識表現
1965年頃、スタンフォード大学のコーデル・グリーンが、節形式(clausal form)のプログラムとその導出原理を考案した。これはジョン・アラン・ロビンソンの命題論理の単一化の演繹法を参考にしていた。1967年にアバディーン大学で開発された言語「Absys」は最初期の論理プログラミングとして知られている。
1960年代の論理プログラミングの進展を通して、数理論理学に忠実な宣言的知識表現と、最適化アルゴリズムを取り入れる手続き的知識表現のどちらを指針にするべきかという議題が提起されていた。宣言的の支持者は、スタンフォード大学とエディンバラ大学中心のジョン・アラン・ロビンソン、コーデル・グリーン、バートラム・ラファエル、パット・ヘイズ、ロバート・コワルスキらであった。手続き的の支持者は、マサチューセッツ工科大学中心のマービン・ミンスキー、シーモア・パパート、カール・ヒューイット、ジェラルド・サスマン、テリー・ウィノグラード、ユージン・チャニアクらであった。
Plannerの登場
1969年、カール・ヒューイット設計の論理型言語「Planner」がマサチューセッツ工科大学で開発された。メインフレーム前提のPlannerの大規模さは運用できる環境を制限したので、1971年にポータビリティ重視のサブセット版「Micro-Planner」が、ジェラルド・サスマンとテリー・ウィノグラードらによって開発された。
1971年、パパート、サスマン、チャニアクらのMIT勢が、エディンバラ大学を訪問してMicro-PlannerとSHRDLUを披露した。当時の同大学は、対話型自動定理証明プロジェクト「Logic for computable functions」が始動されていた論理プログラミングのメッカであった。Micro-Plannerなどを見たパット・ヘイズらは手続き的の価値を認め、同大学でもMicro-Plannerのサブセット版を実装してその有用性を確認した。Plannerを研究したロバート・コワルスキは、アルフレッド・ホーン発案のホーン節の論理プログラミング導入を提唱し、それへのSLD導出を考案している。更にエディンバラ大学ではPlannerのスーパーセット版「Popler」も開発された。
Prologの登場
1972年、マルセイユ大学のアラン・カルメラウアーらは、ロバート・コワルスキーらの助言を得てホーン節とSLD導出をベースにした論理型言語「Prolog」を開発した。Prologに対する意見は分かれ、カール・ヒューイットなどはMicro-Plannerの複製品であると言い、コワルスキは論理プログラミングへの良いアプローチであると評した[2]。カルメラウアーの元祖版は「Marseille Prolog」と呼ばれる。コワルスキの門弟デビッド・ウォーレンのエディンバラ大学開発版は「Edinburgh Prolog」と呼ばれ、その系譜の1977年開発版「DEC-10 Prolog」がPrologの標準形になった。1979年にコワルスキはインペリアル・カレッジ・ロンドンで論理プログラミング基礎大全『Logic for Problem Solving』を上梓した。
1983年、ウォーレンはSRIインターナショナルでProlog言語処理系標準モデルのウォーレン抽象マシンを策定し、Prologの普及に努めた。1986年に論理プログラミング協会が設立された。1987年にDEC-10系譜の「SWI-Prolog」がアムステルダム大学のジャン・ウィールメーカーによって開発され、これが現在最も使われているPrologになっている。
1980年代の日本の情報工学分野ではProlog研究が盛んに行われており、人工知能コンピュータ開発を目的にした第五世代コンピュータ計画の中心になっていた。
特徴
論理と制御
論理プログラミングでは「ロジック(論理)+コントロール(制御)=アルゴリズム(算法)」とされている。ロジックとは、数理論理学の論理式を特定の解釈で投影したプログラム書式表現を指す。これの代表例はファクト(事実)とルール(規則)を列挙するものであり、ルールは論理包含を主体にする。コントロールとは、そのロジックに対して、一定のファクトまたは特定のゴール(目標)を起点にした任意の問題条件を与えて、一定の解決条件を導出(resolution)することを指す。これを問題解決と言う。ロジックとコントロールの融合は、多様な定理証明戦略を表現する[3]。
最も普及しているProlog系の論理プログラムで使われる導出原理は、論理式をこれ以上解消できない所まで変形させていく演繹や簡約である。そこでのロジックはホーン節で表現されており、コントロールにはSLD導出が使われている。
問題解決

問題解決(problem solving)とその実践の導出原理は、数理論理学の膨大な知識から様々なものが存在する。ここではシンプルなロジックの代表格のホーン節を例にする。ホーン節は最大1個の正リテラルを持つ選言標準形をベースにしており、命題論理のホーン節は、素直にAND-OR木に投影できる。(右図はこの説明には不向きだが、これしか無かったのであしからず)右図のAND-OR木では、最上ノードのPがゴールになり、末端ノードのT・U・R・Sはファクトになって、このように解釈できる。
if Q and R then P, if S then P, if T then Q, if U then Q.
それへの導出原理は、ファクトから問題解決する前向き連鎖と、ゴールから問題解決する後向き連鎖に大別される。前向き連鎖は、与えられたファクトから様々な別のファクトをゴールとして解答する演繹手法である。TとRを与えるとPが解答される。Sを与えるとPが解答される。前向き連鎖はエキスパートシステムなどに使われている。後向き連鎖は、与えられたゴールがファクトかどうかを解答する演繹手法である。Pを与えるとその前件のRおよびQのそのまた前件のTがファクトなのでPはファクトと解答される。後向き連鎖は論理型言語の代表Prologに使われている。
述語論理のホーン節は、AND-OR木の各ノードが命題から述語になるので複雑になる。各ノードの述語記号の項は、定項と変項に分かれるが、定項がファクトで、変項が単一化によるファクトに束縛可能なら、そのノードは述語から命題になれる。
失敗による否定
論理プログラムが節 H :- B1, ..., Bn から構成され、H, B1, ..., Bn が全てアトミックな述語論理式であれば、このプログラムは確定(definite)していると呼ばれ、ホーン節プログラムであるともいう。確定した論理プログラムの手続き的意味と宣言的意味は、そのまま述語論理的に解釈できる。否定を含めると、古典的論理との関係はそれほど直接的ではなくなる。「失敗による否定; negation-as-failure」推論規則によれば、ゴール Q がプログラムによって証明できない場合、その否定 not(Q) は証明されたと見なされる。これは古典的論理学では全く正しくない。公理から Q も not(Q) も導けない可能性がある。結果として、この規則は論理的例外と実用的困難さをもたらした。後方連鎖証明規則に「失敗による否定」を加えても完全ではない。その場合、プログラムを宣言的に読んで得られる論理的結果の全てを証明することができない。しかし、ほとんどの Prolog 系言語は「失敗による否定」を \+ という文字列を使って実装している。
完全ではないものの、プログラムとしての完全性(completion)という意味では「失敗による否定」規則は(ある制限下で)健全な推論規則であると言える。論理プログラムの完全性は Keith Clark が最初に定義した。おおまかに言えば、それはプログラム内の左辺に同じ述語のある全節の集合である。例えば、以下のようなものである:
H :- Body1.
....
H :- Bodyk.
これらは次の1つの論理式と等価である。
H iff (Body1 or ... or Bodyk)
ここで、iff は同値(if and only if)を意味する。完全性を主張するには、等号と等号に関する公理を明確にする必要もある。完全性は非単調推論のためのマッカーシーのサーカムスクリプションや閉世界仮説に密接に関連する。
知識表現
知識表現(knowledge representation)は、宣言的知識と手続き的知識に大別される。例えば「空から水」への知識は、宣言的では「雨」と表現され、そこから手続き的では「傘をさす」などと表現される。俗説になるが宣言的知識はintelligence、手続き的知識はwisdomとも言われる。Prologのホーン節と後向き連鎖のSLD導出と失敗による否定の非単調論理の論理プログラミングは、宣言的知識と手続き的知識の混合とされている。
Prolog
Prolog は 1972年にマルセイユのカルメラウアーが考案し、1974年にコワルスキーがさらに形式的に定義し、数理論理学に基づいた言語として発表した。Prolog のプログラムは一階述語論理のサブセットの論理式の集まりとして読むことができ、一階述語論理のモデル理論と証明理論を継承している。プログラムの節は次のように書かれる:
H :- B1, ..., Bn.
これを宣言として読めば、以下の論理的含意に等しい:
B1 and ... and Bn implies H
ここで、節内の全変数(変項)は全称量化されている。手続き的な後方連鎖規則として見れば、H を証明するには、B1 から Bn までを証明できれば十分であることがわかる。手続き的意味は線形導出法(LUSH または SLD導出法)による反駁証明によっても定式化できる。宣言的意味と手続き的意味の密接な関係は論理プログラミング言語の際立った特徴であるが、否定や論理和といった他の量化子をプログラム内に許すようになると関係は複雑になる。
Prolog の実装
最初に実装された Prolog処理系は1972年に開発された Marseille Prolog である。Prolog が実用的なプログラミング言語として使われるきっかけとなったのは 1977年にエジンバラで David Warren がコンパイラ処理系を開発したことであった。Edinburgh Prolog は他の記号処理言語(Lispなど)と処理速度を比較して遜色ない性能であることを世に示した。Edinburgh Prolog はデファクトスタンダードとなり、後の ISO での Prolog 標準化に影響を与えた。
派生分野
並行論理プログラミング
Keith Clark、Hervé Gallaire、Steve Gregory、Vijay Saraswat、Udi Shapiro、Kazunori Ueda(上田和紀)らは、共有変数のユニフィケーション機能とメッセージのためのデータ構造ストリーム機能を備えた並行論理プログラミング言語を開発した。数理論理学に基づく並行プログラミングの基礎を築くための研究であるが、これが第五世代コンピュータの基盤ともなった。
並行論理プログラミングは制約論理プログラミングと結び付き、制約で並行実行を制御する並行制約プログラミングとして統合され、 Saraswatらにより理論化が行われた。KahnとSaraswatは並行制約プログラミングの枠内での制約の設定でアクターモデルが実現できることから、アクターモデルは並行制約プログラミングの特別なケースだと主張した[4]。
- Concurrent Prolog、PARLOG、GHC、KL1
- Oz、Alice、ToonTalk
制約論理プログラミング
述語記号の項に、制約も含めるようにしている。制約(constraint)とは値(元・要素・個体)を”関係性”で表現したものであり、決定変数の集合で定義される計算対象である。
- B-Prolog、Ciao、ECLiPSe、Fril
高階論理プログラミング
述語記号の項に、述語記号も含めるようにしている。例えば、p(A, B, C) :- q(A, foo), r(B, bar), C.では、Cを別個の述語記号にできる。テンプレートメタ的な書式も扱っており、例えばp(A, B, C) :- (C)(A, B)では、Cが述語名でAとBがその項になる。
- λProlog、HiLog
関数論理プログラミング
述語記号と関数記号の双方をリテラルにしている。
- Mercury、Curry
オブジェクト指向論理プログラミング
ファクトとルールをまとめたモジュールを扱っている。module.predicate(A, B, C)のように表記できる。モジュールは、オブジェクト指向由来の継承と多態性を備えている。既存の上位モジュールを継承して新規の下位モジュールを定義できる。上位モジュールの変数に下位モジュールを代入してサブタイピングするのが多態性である。例えばvar.predicate(A, B, C)では、上位変数varに下位モジュールAを代入するとAのpredicateと解釈され、同変数に下位モジュールBを代入するとBのpredicateと解釈される。
- Visual Prolog
線形論理プログラミング
線形論理を扱っている。
帰納論理プログラミング
仮説論理プログラミング
適用分野
- エキスパートシステム
- 特定応用分野の巨大なモデルから、推奨や回答を生成するプログラム
- 自動定理証明
- 既存の理論から新たな定理を生成するプログラム
関連項目
脚注
- ^ Alain Colmerauer and Philippe Roussel, The birth of Prolog
- ^ a b Robert Kowalski. The Early Years of Logic Programming
- ^ R.A.Kowalski (July 1979). “Algorithm=Logic + Control”. Communications of the ACM 22 (7): 424–436. doi:10.1145/359131.359136.
- ^ Kenneth Kahn, and Viyaj Saraswat, Actors as a Special Case of Concurrent Constraint Programming
参考文献
- Alain Colmerauer and Philippe Roussel, ’The birth of Prolog', in The second ACM SIGPLAN conference on History of programming languages, p. 37-52, 1992.
- John McCarthy. Programs with common sense Symposium on Mechanization of Thought Processes. National Physical Laboratory. Teddington, England. 1958.
- Fisher Black. A deductive question answering system Harvard University. Thesis. 1964.
- James Slagle. Experiments with a Deductive Question-Answering Program CACM. December, 1965.
- Cordell Green. Application of Theorem Proving to Problem Solving IJCAI 1969.
- Carl Hewitt. Planner: A Language for Proving Theorems in Robots IJCAI 1969.
- Gerry Sussman and Terry Winograd. Micro-planner Reference Manual AI Memo No, 203, MIT Project MAC, July 1970.
- Carl Hewitt. Procedural Embedding of Knowledge In Planner IJCAI 1971.
- Terry Winograd. Procedures as a Representation for Data in a Computer Program for Understanding Natural Language MIT AI TR-235. January 1971.
- Bruce Anderson. Documentation for LIB PICO-PLANNER School of Artificial Intelligence, Edinburgh University. 1972
- Bruce Baumgart. Micro-Planner Alternate Reference Manual Stanford AI Lab Operating Note No. 67, April 1972.
- Julian Davies. Popler 1.6 Reference Manual University of Edinburgh, TPU Report No. 1, May 1973.
- Jeff Rulifson, Jan Derksen, and Richard Waldinger. QA4, A Procedural Calculus for Intuitive Reasoning SRI AI Center Technical Note 73, November 1973.
- Robert Kowalski Predicate Logic as a Programming Language Memo 70, Department of Artificial Intelligence, Edinburgh University. 1973.
- Drew McDermott and Gerry Sussman. The Conniver Reference Manual MIT AI Memo 259A. January 1974.
- Earl Sacerdoti, et al. QLISP: A Language for the Interactive Development of Complex Systems AFIPS National Computer Conference. 1976.
- Bill Kornfeld and Carl Hewitt. The Scientific Community Metaphor IEEE Transactions on Systems, Man, and Cybernetics. January 1981.
- Bill Kornfeld. The Use of Parallelism to Implement a Heuristic Search IJCAI 1981.
- Bill Kornfeld. Parallelism in Problem Solving MIT EECS Doctoral Dissertation. August 1981.
- Bill Kornfeld. Combinatorially Implosive Algorithms CACM. 1982
- Carl Hewitt. The Challenge of Open Systems Byte Magazine. April 1985.
- Robert Kowalski. The limitation of logic Proceedings of the 1986 ACM fourteenth annual conference on Computer science.
- Ehud Shapiro (Editor). Concurrent Prolog MIT Press. 1987.
- Robert Kowalski. The Early Years of Logic Programming CACM. January 1988.
- Ehud Shapiro. The family of concurrent logic programming languages ACM Computing Surveys. September 1989.
- Carl Hewitt and Gul Agha. Guarded Horn clause languages: are they deductive and Logical? International Conference on Fifth Generation Computer Systems, Ohmsha 1988. Tokyo. Also in Artificial Intelligence at MIT, Vol. 2. MIT Press 1991.
- Shunichi Uchida and Kazuhiro Fuchi Proceedings of the FGCS Project Evaluation Workshop Institute for New Generation Computer Technology (ICOT). 1992.
- Carl Hewitt. The repeated demise of logic programming and why it will be reincarnated What Went Wrong and Why: Lessons from AI Research and Applications. Technical Report SS-06-08. AAAI Press. March 2006.
- J. W. Lloyd. Foundations of Logic Programming (2nd edition). Springer-Verlag 1987.
- Kenneth Kahn, and Viyaj Saraswat, Actors as a Special Case of Concurrent Constraint Programming, Xerox Technical Report, 1990.
外部リンク
「論理プログラミング」の例文・使い方・用例・文例
論理プログラミングと同じ種類の言葉
- 論理プログラミングのページへのリンク


