ニューラルネットワーク
ニューラルネットワークとは、情報処理の計算モデルのうち、人間の脳の働きを模倣して構築された計算モデルのことである。
ニューラルネットワークのシステムは、比較的単純な処理単位をニューロン(神経細胞)と定義し、多数のニューロンを情報の入出力伝達網で接続した脳の仕組みに似せて構築されている。
ニューラルネットワークは、ニューロコンピュータと呼ばれるコンピュータシステムの計算モデルとなっている。ニューロコンピュータは自己学習を実現することができる新世代の人口知能として、盛んに研究・開発が行われている。
ニューラルネットワーク
生物の神経系の高度な情報処理機構を工学的に模倣し、入力と出力を相互にきめ細かく関連づけて複雑な制御を行う情報処理技術のこと。例えばオートエアコンにこれを導入すると人の感覚に近い綴密な空調制御が可能となる。スイッチや各センサーなどから信号を送る入力層、その情報をもとに入力と出力の優先順位をはかりながら相互関係の調整を行う中間層、それらの総和をもとに必要な制御量を算出してオートエアコン・アンプリファイアに出力する出力層の3種のニューロン(神経細胞)モデルが複数絡み合って、ネットワークを構成している。
参照 オートエアコンニューラルネットワーク
生物の神経系の情報処理を工学的に模倣したもので、人間の脳のように複雑な入力と出力の関係を、相互にきめ細かく関連づけて複雑な制御を行うシステム。トヨタ車のオートエアコンの制御に採用されており、外気温、室温、日射量を感知し、吹出し温度、風量を緻密に制御して乗員の感覚に合わせた、より快適な空調システムとしている。
ニューラルネットワーク
【英】:neural network
概要
(2) 神経回路の構造やニューロン(neuron)の作用を部分的に模倣した, コンピュータや電子回路を用いた人工的な「神経回路網」で, 記憶, 認識, 連想などの機能を実現する工学的なシステムのこと. ノイズに対する頑健性(robustness), 類似入力に対する汎化性(generalization), 学習が容易な高い適応性(adaptability), 並列処理への潜在的可能性をもつ.
詳説
ニューラルネットワーク (neural network) は神経回路網のことであり, その機能をコンピュータや専用ハードウェアで模倣したものを人工ニューラルネットワーク (artificial neural network) という. ORなどの分野で単にニューラルネットワークという場合は, 多くは人工ニューラルネットワークのことを指し, 具体的には比較的単純な非線形信号処理ユニットを結合することで構成されるネットワークのことと考えることが多い. ニューラルネットワークは本質的に並列分散処理的であり, 自己組織的であるといった特徴を内包している.
ニューラルネットワークの歴史を概観すると以下のようになる. 1943年にマッカロック(W. McCulloch)とピッツ(W. Pitts) [1] によるしきい値素子モデルが提案された. 1949年の心理学者D. Hebbの "The Organization of Behavior" [2] において示されたシナプス強化則とも言われる学習方法に関する考え方は, その後提案された多くのニューラルネットの学習方法の基礎となっている. 1962年, ローゼンブラット(F. Rosenblatt)によるパーセプトロン [3] (perceptron) が提案されたが, 1969年, ミンスキー(M. Minsky)とパパート(S. Papert)によるパーセプトロンの限界の呈示, 何人かの研究者による初期バージョンの後, 1986年にラメルハート(D. Rumelhart), ヒントン(G. Hinton), ウイリアムス(R. Williams)によりまとめられた階層型ニューラルネットワークの誤差逆伝播法 (back propagation) の定式化 [4] などを経て, 近年は, 脳の機能の実現を強く意識した研究も盛んに行われている.
ニューラルネットワークは2つの側面から最適化と関係が深い. まず1つは, ニューラルネットワークの機能としての最適化, もう1つは, 何らかの機能を実現するためのニューラルネットワークの学習における最適化である.
ホップフィールドネットワーク [5] (Hopfield network) は, 連想記憶を行ったり巡回セールスマン問題などの最適化問題を解くために考え出されたニューラルネットワークで, 1982年, ホップフィールド (J. J. Hopfield) により提案された. 記憶したいパターン情報は定係数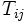 の中に埋めこまれる. このモデルは1984年, 連続値モデルに拡張された. 離散および連続モデルを合わせてホップフィールドネットワークと呼ばれる. ホップフィールドとタンク(T. W. Tank)は1985年に, ホップフィールドネットワークを巡回セールスマン問題の解法に用いる方法を示し [6] , ニューラルネットワークの最適化への応用の道を開いた.
の中に埋めこまれる. このモデルは1984年, 連続値モデルに拡張された. 離散および連続モデルを合わせてホップフィールドネットワークと呼ばれる. ホップフィールドとタンク(T. W. Tank)は1985年に, ホップフィールドネットワークを巡回セールスマン問題の解法に用いる方法を示し [6] , ニューラルネットワークの最適化への応用の道を開いた.
ニューラルネットワークによる学習は, 教師あり学習, 教師なし学習に大別される. 教師あり学習とは, サンプルデータにおいて, 入力値に対して出力値が与えられ, 多数の入出力組の関係を同時に実現するようにモデルの中のパラメータを調整するモデルであり, その用途としては, 分類及び非線形回帰がある. この2つの本質的な違いは教師出力信号として2値信号を用いるか実数値を用いるかという点である. パーセプトロン, 階層型ネットワーク, RBF (radial basis function) ネットワークなどがあり, データのクラス判定や非線形関数近似を行うモデルを, 例 (examples) としてのデータから構築する. しきい値関数を使ったモデルでは, パーセプトロンなどのように, 誤り訂正学習が用いられる. また, ロジスティック (logistic) 関数などの微分可能関数を用いたモデルでは, 二乗誤差を最小化するような評価関数が学習に用いられる. 階層型ニューラルネットに二乗誤差最小化を取り入れると, 誤差逆伝播法が導かれる. 教師なし学習とは, 入力ベクトルだけがあるもので, 入力ベクトルに関する分布の情報を学習するものであり, 情報圧縮, 確率密度関数モデルを用いた推論などに応用される. コホネン(T. Kohonen)の自己組織化マップ (self organizing map), ガウス混合モデル (Gaussian mixture model), k-meansクラスタリングなどが代表的な例である.
人工知能においては, 記号論理をベースにしたシンボリストモデル (symbolist model) に対し, ニューラルネットワークの相互結合をもじったコネクショニストモデル (connectionist model) は, 相互に対極にあるものとして対比されてきた. シンボリストモデルは論理的な説明に適しており, コネクショニストモデルは学習が容易であるという特長を持つ反面, 一般にシンボリストモデルは学習が困難であり, コネクショニストモデルは説明能力に欠けるということがいえる. コネクショニストモデルが説明能力に欠けるというのは, 入力空間を自在に切り分けることができるがゆえにその複雑な切り口を言語的に説明することが困難なためであり, 欠点というよりもそのモデルの持つ特質からくる特徴であって, 特に言語的な説明を要しない制御などの分野では明らかに優れた能力を発揮する. また, 日々の売上データから顧客の特徴を抽出したり, クレジットカードの入会審査を行ったりするデータマイニング(data mining)の分野においても有力な手法として注目されている.
[1] W. W. McCulloch and W. Pitts, "A Logical Calculus of the Ideas Immanent in Nervous Activity," Bull. Math. Biophysics, 5 (1943), 115-133.
[2] A. O. Hebb, The Organization of Behavior, Wiley, 1949. 白井 訳, 『行動の機構』, 岩波書店, 1957.
[3] F. Rosenblatt, Principles of Neurodynamics, Spartan, 1962.
[4] D. E. Rumelhart, G. E. Hinton and R. J. Williams, "Learning Internal Representation by Error Propagation", in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, Parallel Distributed Processing: Explorations in the Microstructure of Cognition, 1, Foundations, MIT Press, 1986. 甘利(監訳), 『PDPモデル-認知科学とニューロン回路網の探索-』, 産業図書, 1989.
[5] J. J. Hopfield, "Neural Networks and Physical Systems with Emergent Collective Computational Abilities," in Proceedings of the National Academy of Sciences U.S.A., 79, 2554-2558, 1982.
[6] J. J. Hopfield and T. W. Tank, "Neural Computation of Decisions in Optimization Problems," Biological Cybernetics, 52 (1985), 141-152.
| 近似・知能・感覚的手法: | デンプスター・シェファーの証拠理論 データマイニング ナップサック問題 ニューラルネットワーク ニューラルネットワークによる学習 ファジィランダム変数 ファジィ推論 |
ニューラルネットワーク
(Neural network から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/07/16 18:10 UTC 版)
| 機械学習および データマイニング |
|---|
 |
| |
人工知能の分野におけるニューラルネットワーク(英: neural network; NN、神経網)は、生物の学習メカニズムを模倣した機械学習手法として広く知られているものであり[1]、「ニューロン」と呼ばれる計算ユニットをもち、生物の神経系のメカニズムを模倣しているものである[1]。人間の脳の神経網を模した数理モデル[2]。模倣対象となった生物のニューラルネットワーク(神経網)とはっきり区別する場合は、人工ニューラルネットワーク (英: artificial neural network) と呼ばれる。
以下では説明の都合上[注釈 1]、人工的なニューラルネットワークのほうは「人工ニューラルネットワーク」あるいは単に「ニューラルネットワーク」と呼び、生物のそれは「生物のニューラルネットワーク」あるいは「生物の神経網」、ヒトの頭脳のそれは「ヒトのニューラルネットワーク」あるいは「ヒトの神経網」と表記することにする。
概要

人工ニューラルネットワークを理解するには、そもそもそれがどのようなものを模倣しようとしているのかを知っておく必要があるので説明する。ヒトの神経系にはニューロンという細胞があり、ニューロン同士は互いに軸索 (axon) と樹状突起 (dendrite) を介して繋がっている。ニューロンは樹状突起で他の神経細胞から情報を受け取り、細胞内で情報処理してから、軸索で他のニューロンに情報を伝達する[3]。そして、軸索と樹状突起が結合する部分をシナプス(synapse)という[3][1](右図も参照。クリックして拡大して見ていただきたい。紫色の部分がひとつのニューロンであり、Dendrite, Axonなどが示されている。)。 このシナプスの結合強度というのは、外的な刺激に反応してちょくちょく変化する。このシナプス結合強度の変化こそが生物における「学習」のメカニズムである[1]。[注釈 2]

ヒトの神経網を模した人工ニューラルネットワークでは、計算ユニットが《重み》を介して繋がり、この《重み》がヒトの神経網のシナプス結合の「強度」と似た役割を担っている[1]。各ユニットへの入力は《重み》によって強さが変化するように作られており、ユニットにおける関数計算に影響を与える。ニューラルネットワークというのは、入力用ニューロンから出力用ニューロンへと向かって計算値を伝播させてゆくが、その過程で《重み》をパラメータとして利用し、入力の関 数を計算する。(ただし計算値が出力用ニューロンへと伝播されてゆくというだけでは入力パターンからある決まった出力パターンが出るだけなので、さほど有益というわけではない[4]。)《重み》が変化することで「学習」が起きる[1](ここが重要なのである[4])。
- (右図も参照のこと。右図で「weights」や、丸で囲まれた「w」が縦に並んでいるのが《重み》である。)
生物のニューラルネットワークに与えられる外的刺激に相当するものとして、人工ニューラルネットワークでは「訓練データ」が与えられる[1]。いくつか方法があるが、たとえば訓練データとして入力データと出力ラベルが与えられ、たとえば何かの画像データとそれについての正しいラベルが与えられる(たとえばリンゴの画像データとappleというラベル、オレンジの画像データとorangeというラベルが与えられる)。ある入力に対して予測される出力が本当のラベルとどの程度一致するかを計算することで、ニューラルネットワークの《重み》についてフィードバックを得られ[1]、ニューロン間の《重み》は誤差(予測誤差)に応じて、誤差が減少するように調整される[1]。多数のニューロン間で《重み》の調整を繰り返し行うことで次第に計算関数が改善され、より正確な予測をできるようになる。(たとえばオレンジの画像データを提示されると「orange」と正しいラベルを答えられるようになる[1]。) 《重み》の調整方法の代表的なものがバックプロパゲーションである[4]。
なお、ヒトのニューロンを模したユニットは人工ニューロンあるいはノードと呼ばれる。

右図の、多数のユニットが結合しネットワークを構成している数理モデルは、ニューラルネットワークのほんの一例である。(実際にはニューロンの数もさまざまに設定可能であるし、結合のしかたもさまざまに設定可能である。右図はあくまで、とりあえず説明にとりかかるための "一例" と理解いただきたい。 ユニットの構成(例: 線形変換の次元、非線形変換の有無・種類)やネットワークの構造(例: ユニットの数・階層構造・相互結合、入出力の再帰)に関して様々な選択肢があり、様々なモデルが提唱されている。)
各ユニットは入力の線形変換を必ず含み、多くの場合それに後続する非線形変換を含む(
順伝播型ニューラルネットワーク
順伝播型ニューラルネットワーク(フィードフォワードニューラルネットワーク、英: Feed-forward Neural Network; FFN, FFNN)は内部に循環を持たないニューラルネットワークの総称・クラスである[125]。
ニューラルネットワークではしばしば層(レイヤ)の概念を取り入れる。FFNでは入力レイヤ→中間レイヤ→出力レイヤというように単一方向/順方向へのみ信号が伝播する。これは回帰型ニューラルネットワークと対比される。層間の結合様式により様々なニューラルネットワークが存在するが、結合様式に関わらず回帰結合を持たないものはすべてFFNに属する。以下はFFNの一例である。
- 単純パーセプトロン: 1-layer 層間全結合ネットワーク
- 多層パーセプトロン: N-layer 層間全結合ネットワーク
- 畳み込みニューラルネットワーク: N-layer 層間局所結合ネットワーク(c.f. recurrent CNN; RCNN)
並列計算
FFNがもつ特徴に並列計算がある。回帰結合をもつネットワークはシーケンシャルに処理を繰り返す必要があるため、1データに対して時間方向に並列計算できない[126]。FFNは層内で並列計算が可能であり、RNNと比較して容易に並列計算機(例: GPU)の計算能力を上限まで引き出せる[注釈 4]。

RBFネットワーク
誤差逆伝播法に用いられる活性化関数に放射基底関数を用いたニューラルネットワーク
- RBFネットワーク
- 一般回帰ニューラルネットワーク(GRNN、General Regression Neural Network)- 正規化したRBFネットワーク
自己組織化写像
自己組織化写像はコホネンが1982年に提案した教師なし学習モデルであり、多次元データのクラスタリング、可視化などに用いられる。自己組織化マップ、コホネンマップとも呼ばれる。
- 自己組織化写像
- 学習ベクトル量子化

畳み込みニューラルネットワーク
畳み込みニューラルネットワークとは層間が全結合ではない順伝播型ニューラルネットワークの一種。画像を対象とするために用いられることが多い。
再帰型ニューラルネットワーク(リカレントニューラルネット、フィードバックニューラルネット)
フィードフォワードニューラルネットと違い、双方向に信号が伝播するモデル。すべてのノードが他の全てのノードと結合を持っている場合、全結合リカレントニューラルネットと呼ぶ。シーケンシャルなデータに対して有効で、自然言語処理や音声、動画の解析などに利用される[127]。
Transformer
Self-Attention機構(自己注意機構)を利用したモデルである[126]。再帰型ニューラルネットワークの代替として考案された[126]。
従来の自然言語処理用モデルに比べ計算量が少なく構造も単純なため、自然言語処理に使われることが多い[128]。
確率的ニューラルネット
乱数による確率的な動作を導入した人工ニューラルネットワークモデル。モンテカルロ法のような統計的標本抽出手法と考えることができる。
スパイキングニューラルネットワーク
ニューラルネットワークをより生物学的な脳の働きに近づけるため、活動電位(スパイク)を重視して作られた人工ニューラルネットワークモデル。スパイクが発生するタイミングを情報と考える。ディープラーニングよりも扱える問題の範囲が広い次世代技術と言われている。ニューラルネットワークの処理は逐次処理のノイマン型コンピュータでは処理効率が低く、活動電位まで模倣する場合には処理効率がさらに低下するため、実用する際には専用プロセッサとして実装される場合が多い。
2015年現在、スパイキングNN処理ユニットを積んだコンシューマー向けのチップとしては、QualcommのSnapdragon 820が登場する予定となっている[129][130]。
複素ニューラルネットワーク
入出力信号やパラメータ(重み、閾値)が複素数値であるようなニューラルネットワークで活性化関数は必然的に複素関数になる[131]。
利点
- 情報の表現
- 入力信号と出力信号が複素数(2次元)であるため、複素数で表現された信号はもとより、2次元情報を自然に表現可能[131]。また特に波動情報(複素振幅)を扱うのに適した汎化能力(回転と拡大縮小)を持ち、エレクトロニクスや量子計算の分野に好適である。四元数ニューラルネットワークは3次元の回転の扱いに優れるなど、高次複素数ニューラルネットワークの利用も進む。
- 学習特性
- 階層型の複素ニューラルネットワークの学習速度は、実ニューラルネットワークに比べて2〜3倍速く、しかも必要とするパラメータ(重みと閾値)の総数が約半分で済む[注釈 5][131]。学習結果は波動情報(複素振幅)を表現することに整合する汎化特性を示す[132]。
生成モデル/統計モデル
生成モデル(統計モデルとも)は、データが母集団の確率分布に従って生成されると仮定しそのパラメータを学習するニューラルネットワークの総称である。統計的機械学習の一種といえる。モデル(=母集団)からのサンプリングによりデータ生成が可能な点が特徴である(詳しくは推計統計学 § 統計モデル、機械学習 § 統計的機械学習)。
自己回帰型生成ネット

スパース化(英: Sparsification)はニューラルネットワークの重みを疎行列とする最適化である。スパース化は精度の低下と速度の向上をもたらす。
スパース化の効果は以下の要素から生み出される。
- キャッシュ: 容量低下によるキャッシュへ乗るデータ量増加 → キャッシュヒット率向上
- メモリ: 容量低下によるメモリ消費とメモリ転送量の減少
- 数値精度: 小さい値のゼロ近似によるモデル出力精度の低下
- 計算量: ゼロ重みとの積省略による計算量の減少
スパース化の恩恵を受けるためにはそのためのフォーマットや演算が必要になる。ゼロ要素を省略する疎行列形式、疎行列形式に対応した演算実装などが挙げられる。またスパース化を前提として精度低下を防ぐよう学習する手法が存在する。
より広い意味での重み除去は枝刈り(英: Pruning)と呼ばれる。枝刈りでは行列のスパース化のみでなく、チャネルやモジュール自体の削除(ゼロ近似)を含む。
脚注
注釈
- ^ 用語が繰り返されるので。
- ^ ニューラルネットワークという用語はもともとは生物の神経網(神経系)を指している。網(ネットワーク)と形容されるのは、実際、網のように広がっているからである。1つの神経細胞は他の神経細胞からの入力をシナプスで重み付けして受け取り、細胞体等での処理を介して、次の複数の神経細胞へと出力する。これらの結合により神経細胞群は全体としてネットワークを形成する。数理モデル化すると、ニューロンは入力の線形変換を含む1つの処理単位であり、これがネットワークを形成しているということになる。
- ^ 2020年現在のところ、「小脳パーセプトロン説」が支持されるなど、「全く無関係」ではない、とされている。
- ^ RNNの場合、巨大バッチを用いて1stepの計算量を巨大にすればGPUを使いきれるが、実践的にはメモリ上限等の制約が厳しい。
- ^ 複素逆誤差伝播学習アルゴリズム(複素BP)を使用した場合。
出典
- ^ a b c d e f g h i j Charu C.Aggarwal著『ニューラルネットワークとディープラーニング』(データサイエンス大系シリーズ)、学術図書出版社、2022年。ISBN 978-4780607147, 第一章「ニューラルネットワークとは」「はじめに」、pp.1-2
- ^ 『2020年版 基本情報技術者 標準教科書』オーム社、p.55
- ^ a b 平塚秀雄『よくわかる脳神経外科学』金原出版、1996, pp.14-15「神経細胞とニューロン」
- ^ a b c 平野廣美「学習することは重みが変わること」『C++とJavaでつくるニューラルネットワーク』パーソナルメディア株式会社、2008年、27頁。 ISBN 978-4-89362-247-1。
- ^ Mansfield Merriman, "A List of Writings Relating to the Method of Least Squares"
- ^ Stigler, Stephen M. (1981). “Gauss and the Invention of Least Squares”. Ann. Stat. 9 (3): 465–474. doi:10.1214/aos/1176345451.
- ^ Bretscher, Otto (1995). Linear Algebra With Applications (3rd ed.). Upper Saddle River, NJ: Prentice Hall
- ^ a b c d e f g h Schmidhuber, Jürgen (2022). “Annotated History of Modern AI and Deep Learning”. arXiv:2212.11279 [cs.NE].
- ^ Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Cambridge: Harvard. ISBN 0-674-40340-1
- ^ a b McCulloch, Warren S.; Pitts, Walter (December 1943). “A logical calculus of the ideas immanent in nervous activity”. The Bulletin of Mathematical Biophysics 5 (4): 115–133. doi:10.1007/BF02478259. ISSN 0007-4985. オリジナルの2024-10-12時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Kleene, S.C. (1956年). “Representation of Events in Nerve Nets and Finite Automata”. Annals of Mathematics Studies (Princeton University Press) (34): pp. 3–41. オリジナルの2024年5月19日時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Hebb, Donald (1949). The Organization of Behavior. New York: Wiley. ISBN 978-1-135-63190-1
- ^ a b c 平野廣美『C++とJavaでつくるニューラルネットワーク』パーソナルメディア株式会社、2008、pp.9-10「はじめに」
- ^ Farley, B.G.; W.A. Clark (1954). “Simulation of Self-Organizing Systems by Digital Computer”. IRE Transactions on Information Theory 4 (4): 76–84. doi:10.1109/TIT.1954.1057468.
- ^ Rochester, N.; J.H. Holland; L.H. Habit; W.L. Duda (1956). “Tests on a cell assembly theory of the action of the brain, using a large digital computer”. IRE Transactions on Information Theory 2 (3): 80–93. doi:10.1109/TIT.1956.1056810.
- ^ Haykin (2008) Neural Networks and Learning Machines, 3rd edition
- ^ Rosenblatt, F. (1958). “The Perceptron: A Probabilistic Model For Information Storage And Organization in the Brain”. Psychological Review 65 (6): 386–408. doi:10.1037/h0042519. PMID 13602029.
- ^ Werbos, P.J. (1975). Beyond Regression: New Tools for Prediction and Analysis in the Behavioral Sciences
- ^ Rosenblatt, Frank (1957). “The Perceptron—a perceiving and recognizing automaton”. Report 85-460-1 (Cornell Aeronautical Laboratory).
- ^ Olazaran, Mikel (1996). “A Sociological Study of the Official History of the Perceptrons Controversy”. Social Studies of Science 26 (3): 611–659. doi:10.1177/030631296026003005. JSTOR 285702.
- ^ a b Joseph, R. D. (1960). Contributions to Perceptron Theory, Cornell Aeronautical Laboratory Report No. VG-11 96--G-7, Buffalo
- ^ Russel, Stuart; Norvig, Peter (2010) (英語). Artificial Intelligence A Modern Approach (3rd ed.). United States of America: Pearson Education. pp. 16–28. ISBN 978-0-13-604259-4
- ^ a b Rosenblatt, Frank (1962). Principles of Neurodynamics. Spartan, New York
- ^ Ivakhnenko, A. G.; Lapa, V. G. (1967). Cybernetics and Forecasting Techniques. American Elsevier Publishing Co.. ISBN 978-0-444-00020-0
- ^ Ivakhnenko, A.G. (March 1970). “Heuristic self-organization in problems of engineering cybernetics” (英語). Automatica 6 (2): 207–219. doi:10.1016/0005-1098(70)90092-0. オリジナルの2024-08-12時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Ivakhnenko, Alexey (1971). “Polynomial theory of complex systems”. IEEE Transactions on Systems, Man, and Cybernetics SMC-1 (4): 364–378. doi:10.1109/TSMC.1971.4308320. オリジナルの2017-08-29時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Robbins, H.; Monro, S. (1951). “A Stochastic Approximation Method”. The Annals of Mathematical Statistics 22 (3): 400. doi:10.1214/aoms/1177729586.
- ^ Amari, Shun'ichi (1967). “A theory of adaptive pattern classifier”. IEEE Transactions EC (16): 279–307.
- ^ Fukushima, K. (1969). “Visual feature extraction by a multilayered network of analog threshold elements”. IEEE Transactions on Systems Science and Cybernetics 5 (4): 322–333. doi:10.1109/TSSC.1969.300225.
- ^ Sonoda, Sho; Murata, Noboru (2017). “Neural network with unbounded activation functions is universal approximator”. Applied and Computational Harmonic Analysis 43 (2): 233–268. arXiv:1505.03654. doi:10.1016/j.acha.2015.12.005.
- ^ Ramachandran, Prajit; Barret, Zoph; Quoc, V. Le (16 October 2017). “Searching for Activation Functions”. arXiv:1710.05941 [cs.NE].
- ^ Minsky, Marvin; Papert, Seymour (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press. ISBN 978-0-262-63022-1
- ^ Bozinovski S. and Fulgosi A. (1976). "The influence of pattern similarity and transfer learning on the base perceptron training" (original in Croatian) Proceedings of Symposium Informatica 3-121-5, Bled.
- ^ Bozinovski S.(2020) "Reminder of the first paper on transfer learning in neural networks, 1976". Informatica 44: 291–302.
- ^ a b Fukushima, K. (1979). “Neural network model for a mechanism of pattern recognition unaffected by shift in position—Neocognitron”. Trans. IECE (In Japanese) J62-A (10): 658–665. doi:10.1007/bf00344251. PMID 7370364.
- ^ Fukushima, K. (1980). “Neocognitron: A self-organizing neural network model for a mechanism of pattern recognition unaffected by shift in position”. Biol. Cybern. 36 (4): 193–202. doi:10.1007/bf00344251. PMID 7370364.
- ^ a b Schmidhuber, J. (2015). “Deep Learning in Neural Networks: An Overview”. Neural Networks 61: 85–117. arXiv:1404.7828. doi:10.1016/j.neunet.2014.09.003. PMID 25462637.
- ^ Leibniz, Gottfried Wilhelm Freiherr von (1920) (英語). The Early Mathematical Manuscripts of Leibniz: Translated from the Latin Texts Published by Carl Immanuel Gerhardt with Critical and Historical Notes (Leibniz published the chain rule in a 1676 memoir). Open court publishing Company. ISBN 9780598818461
- ^ Kelley, Henry J. (1960). “Gradient theory of optimal flight paths”. ARS Journal 30 (10): 947–954. doi:10.2514/8.5282.
- ^ Linnainmaa, Seppo (1970). The representation of the cumulative rounding error of an algorithm as a Taylor expansion of the local rounding errors (Masters) (フィンランド語). University of Helsinki. p. 6–7.
- ^ Linnainmaa, Seppo (1976). “Taylor expansion of the accumulated rounding error”. BIT Numerical Mathematics 16 (2): 146–160. doi:10.1007/bf01931367.
- ^ Ostrovski, G.M., Volin,Y.M., and Boris, W.W. (1971). On the computation of derivatives. Wiss. Z. Tech. Hochschule for Chemistry, 13:382–384.
- ^ a b Schmidhuber, Juergen (2014年10月25日). “Who Invented Backpropagation?”. IDSIA, Switzerland. 2024年7月30日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ Werbos, Paul (1982). “Applications of advances in nonlinear sensitivity analysis”. System modeling and optimization. Springer. pp. 762–770. オリジナルの2016-04-14時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Anderson, James A., ed (2000) (英語). Talking Nets: An Oral History of Neural Networks. The MIT Press. doi:10.7551/mitpress/6626.003.0016. ISBN 978-0-262-26715-1. オリジナルの2024-10-12時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Werbos, Paul J. (1994). The Roots of Backpropagation : From Ordered Derivatives to Neural Networks and Political Forecasting. New York: John Wiley & Sons. ISBN 0-471-59897-6
- ^ a b c 小野田崇、染谷博司「ニューラルネット研究の温故知新と最適化手法の研究動向」『電気学会論文誌C』第130巻第1号、2010年、2-5頁。
- ^ a b c d 國吉康夫「人工知能の将来と人間・社会」『科学技術社会論研究』第16巻、2018年、15-29頁。
- ^ Rumelhart, David E.; Hinton, Geoffrey E.; Williams, Ronald J. (October 1986). “Learning representations by back-propagating errors” (英語). Nature 323 (6088): 533–536. Bibcode: 1986Natur.323..533R. doi:10.1038/323533a0. ISSN 1476-4687. オリジナルの2021-03-08時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Fukushima, Kunihiko; Miyake, Sei (1 January 1982). “Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position”. Pattern Recognition 15 (6): 455–469. Bibcode: 1982PatRe..15..455F. doi:10.1016/0031-3203(82)90024-3. ISSN 0031-3203. オリジナルの2024-10-12時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Waibel, Alex (December 1987). Phoneme Recognition Using Time-Delay Neural Networks (PDF). Meeting of the Institute of Electrical, Information and Communication Engineers (IEICE). Tokyo, Japan. 2024年9月17日時点のオリジナルよりアーカイブ (PDF). 2025年6月20日閲覧.
- ^ Alexander Waibel et al., Phoneme Recognition Using Time-Delay Neural Networks Archived 2024-12-11 at the Wayback Machine. IEEE Transactions on Acoustics, Speech, and Signal Processing, Volume 37, No. 3, pp. 328. – 339 March 1989.
- ^ Zhang, Wei (1988). “Shift-invariant pattern recognition neural network and its optical architecture”. Proceedings of Annual Conference of the Japan Society of Applied Physics. オリジナルの2020-06-23時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ LeCun et al., "Backpropagation Applied to Handwritten Zip Code Recognition", Neural Computation, 1, pp. 541–551, 1989.
- ^ LeCun, Yann; Léon Bottou; Yoshua Bengio; Patrick Haffner (1998). “Gradient-based learning applied to document recognition”. Proceedings of the IEEE 86 (11): 2278–2324. doi:10.1109/5.726791. オリジナルの2023-10-30時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Zhang, Wei (1990). “Parallel distributed processing model with local space-invariant interconnections and its optical architecture”. Applied Optics 29 (32): 4790–7. Bibcode: 1990ApOpt..29.4790Z. doi:10.1364/AO.29.004790. PMID 20577468. オリジナルの2017-02-06時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Zhang, Wei (1991). “Image processing of human corneal endothelium based on a learning network”. Applied Optics 30 (29): 4211–7. Bibcode: 1991ApOpt..30.4211Z. doi:10.1364/AO.30.004211. PMID 20706526. オリジナルの2024-06-19時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Zhang, Wei (1994). “Computerized detection of clustered microcalcifications in digital mammograms using a shift-invariant artificial neural network”. Medical Physics 21 (4): 517–24. Bibcode: 1994MedPh..21..517Z. doi:10.1118/1.597177. PMID 8058017. オリジナルの2024-06-20時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Qian, Ning, and Terrence J. Sejnowski. "Predicting the secondary structure of globular proteins using neural network models." Journal of molecular biology 202, no. 4 (1988): 865–884.
- ^ Bohr, Henrik, Jakob Bohr, Søren Brunak, Rodney MJ Cotterill, Benny Lautrup, Leif Nørskov, Ole H. Olsen, and Steffen B. Petersen. "Protein secondary structure and homology by neural networks The α-helices in rhodopsin." FEBS letters 241, (1988): 223–228
- ^ Rost, Burkhard, and Chris Sander. "Prediction of protein secondary structure at better than 70% accuracy." Journal of molecular biology 232, no. 2 (1993): 584–599.
- ^ Amari, S.-I. (November 1972). “Learning Patterns and Pattern Sequences by Self-Organizing Nets of Threshold Elements”. IEEE Transactions on Computers C-21 (11): 1197–1206. doi:10.1109/T-C.1972.223477. ISSN 0018-9340. オリジナルの2024-10-12時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Hopfield, J. J. (1982). “Neural networks and physical systems with emergent collective computational abilities”. Proceedings of the National Academy of Sciences 79 (8): 2554–2558. Bibcode: 1982PNAS...79.2554H. doi:10.1073/pnas.79.8.2554. PMC 346238. PMID 6953413.
- ^ Espinosa-Sanchez, Juan Manuel; Gomez-Marin, Alex; de Castro, Fernando (5 July 2023). “The Importance of Cajal's and Lorente de Nó's Neuroscience to the Birth of Cybernetics” (英語). The Neuroscientist 31 (1): 14–30. doi:10.1177/10738584231179932. hdl:10261/348372. ISSN 1073-8584. PMID 37403768. オリジナルの2024-10-12時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ “reverberating circuit”. Oxford Reference. 2024年10月12日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ a b Bozinovski, S. (1982). "A self-learning system using secondary reinforcement". In Trappl, Robert (ed.). Cybernetics and Systems Research: Proceedings of the Sixth European Meeting on Cybernetics and Systems Research. North-Holland. pp. 397–402. ISBN 978-0-444-86488-8
- ^ Bozinovski S. (1995) "Neuro genetic agents and structural theory of self-reinforcement learning systems". CMPSCI Technical Report 95-107, University of Massachusetts at Amherst [1] Archived 2024-10-08 at the Wayback Machine.
- ^ R. Zajonc (1980) "Feeling and thinking: Preferences need no inferences". American Psychologist 35 (2): 151-175
- ^ Lazarus R. (1982) "Thoughts on the relations between emotion and cognition" American Psychologist 37 (9): 1019-1024
- ^ Bozinovski, S. (2014) "Modeling mechanisms of cognition-emotion interaction in artificial neural networks, since 1981" Procedia Computer Science p. 255-263 (https://core.ac.uk/download/pdf/81973924.pdf Archived 2019-03-23 at the Wayback Machine.)
- ^ Schmidhuber, Jürgen (April 1991). “Neural Sequence Chunkers”. TR FKI-148, TU Munich. オリジナルの2024-09-14時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Schmidhuber, Jürgen (1992). “Learning complex, extended sequences using the principle of history compression (based on TR FKI-148, 1991)”. Neural Computation 4 (2): 234–242. doi:10.1162/neco.1992.4.2.234. オリジナルの2024-09-14時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Schmidhuber, Jürgen (1993). Habilitation thesis: System modeling and optimization. オリジナルの2024-08-07時点におけるアーカイブ。 2025年6月20日閲覧。 Page 150 ff demonstrates credit assignment across the equivalent of 1,200 layers in an unfolded RNN.
- ^ a b S. Hochreiter., "Untersuchungen zu dynamischen neuronalen Netzen", Archived 2015-03-06 at the Wayback Machine., Diploma thesis. Institut f. Informatik, Technische Univ. Munich. Advisor: J. Schmidhuber, 1991.
- ^ Hochreiter, S. (15 January 2001). “Gradient flow in recurrent nets: the difficulty of learning long-term dependencies”. A Field Guide to Dynamical Recurrent Networks. John Wiley & Sons. ISBN 978-0-7803-5369-5. オリジナルの2024-05-19時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ ゼップ・ホッフライター [英語版]; ユルゲン・シュミットフーバー [英語版] (21 August 1995), Long Short Term Memory (英語), Wikidata Q98967430
- ^ Hochreiter, Sepp; Schmidhuber, Jürgen (1 November 1997). “Long Short-Term Memory”. Neural Computation 9 (8): 1735–1780. doi:10.1162/neco.1997.9.8.1735. PMID 9377276.
- ^ Gers, Felix; Schmidhuber, Jürgen; Cummins, Fred (1999). “Learning to forget: Continual prediction with LSTM”. 9th International Conference on Artificial Neural Networks: ICANN '99. 1999. pp. 850–855. doi:10.1049/cp:19991218. ISBN 0-85296-721-7
- ^ Ackley, David H.; Hinton, Geoffrey E.; Sejnowski, Terrence J. (1 January 1985). “A learning algorithm for boltzmann machines”. Cognitive Science 9 (1): 147–169. doi:10.1016/S0364-0213(85)80012-4. ISSN 0364-0213. オリジナルの2024-09-17時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Smolensky, Paul (1986). “Chapter 6: Information Processing in Dynamical Systems: Foundations of Harmony Theory”. In Rumelhart, David E.; McLelland, James L.. Parallel Distributed Processing: Explorations in the Microstructure of Cognition, Volume 1: Foundations. MIT Press. pp. 194–281. ISBN 0-262-68053-X. オリジナルの2023-07-14時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Peter, Dayan; Hinton, Geoffrey E.; Neal, Radford M.; Zemel, Richard S. (1995). “The Helmholtz machine.”. Neural Computation 7 (5): 889–904. doi:10.1162/neco.1995.7.5.889.
hdl:21.11116/0000-0002-D6D3-E.
PMID 7584891.

- ^ Hinton, Geoffrey E.; Dayan, Peter; Frey, Brendan J.; Neal, Radford (26 May 1995). “The wake-sleep algorithm for unsupervised neural networks”. Science 268 (5214): 1158–1161. Bibcode: 1995Sci...268.1158H. doi:10.1126/science.7761831. PMID 7761831.
- ^ a b Reducing the Dimensionality of Data with Neural Networks
- ^ a b A fast learning algorithm for deep belief nets
- ^ 2012 Kurzweil AI Interview Archived 2018-08-31 at the Wayback Machine. with Juergen Schmidhuber on the eight competitions won by his Deep Learning team 2009–2012
- ^ “How bio-inspired deep learning keeps winning competitions”. kurzweilai.net. 2018年8月31日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ Cireşan, Dan Claudiu; Meier, Ueli; Gambardella, Luca Maria; Schmidhuber, Jürgen (21 September 2010). “Deep, Big, Simple Neural Nets for Handwritten Digit Recognition”. Neural Computation 22 (12): 3207–3220. arXiv:1003.0358. doi:10.1162/neco_a_00052. ISSN 0899-7667. PMID 20858131.
- ^ Ciresan, D. C.; Meier, U.; Masci, J.; Gambardella, L.M.; Schmidhuber, J. (2011). “Flexible, High Performance Convolutional Neural Networks for Image Classification”. International Joint Conference on Artificial Intelligence. doi:10.5591/978-1-57735-516-8/ijcai11-210. オリジナルの2014-09-29時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Ciresan, Dan; Giusti, Alessandro; Gambardella, Luca M.; Schmidhuber, Jürgen (2012). Pereira, F.. ed. Advances in Neural Information Processing Systems 25. Curran Associates, Inc.. pp. 2843–2851. オリジナルの2017-08-09時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Ciresan, D.; Giusti, A.; Gambardella, L.M.; Schmidhuber, J. (2013). “Mitosis Detection in Breast Cancer Histology Images with Deep Neural Networks”. Medical Image Computing and Computer-Assisted Intervention – MICCAI 2013. Lecture Notes in Computer Science. 7908. pp. 411–418. doi:10.1007/978-3-642-40763-5_51. ISBN 978-3-642-38708-1. PMID 24579167
- ^ Ciresan, D.; Meier, U.; Schmidhuber, J. (2012). “Multi-column deep neural networks for image classification”. 2012 IEEE Conference on Computer Vision and Pattern Recognition. pp. 3642–3649. arXiv:1202.2745. doi:10.1109/cvpr.2012.6248110. ISBN 978-1-4673-1228-8
- ^ Krizhevsky, Alex; Sutskever, Ilya; Hinton, Geoffrey (2012). “ImageNet Classification with Deep Convolutional Neural Networks”. NIPS 2012: Neural Information Processing Systems, Lake Tahoe, Nevada. オリジナルの2017-01-10時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Simonyan, Karen; Andrew, Zisserman (2014). “Very Deep Convolution Networks for Large Scale Image Recognition”. arXiv:1409.1556 [cs.CV].
- ^ Szegedy, Christian (2015). “Going deeper with convolutions”. Cvpr2015. arXiv:1409.4842. オリジナルの2024-09-30時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Ng, Andrew; Dean, Jeff (2012). “Building High-level Features Using Large Scale Unsupervised Learning”. arXiv:1112.6209 [cs.LG].
- ^ Ian Goodfellow and Yoshua Bengio and Aaron Courville (2016). Deep Learning. MIT Press. オリジナルの16 April 2016時点におけるアーカイブ。 2016年6月1日閲覧。
- ^ Billings, S. A. (2013). Nonlinear System Identification: NARMAX Methods in the Time, Frequency, and Spatio-Temporal Domains. Wiley. ISBN 978-1-119-94359-4
- ^ Goodfellow, Ian; Pouget-Abadie, Jean; Mirza, Mehdi; Xu, Bing; Warde-Farley, David; Ozair, Sherjil; Courville, Aaron; Bengio, Yoshua (2014). Generative Adversarial Networks (PDF). Proceedings of the International Conference on Neural Information Processing Systems (NIPS 2014). pp. 2672–2680. 2019年11月22日時点のオリジナルよりアーカイブ (PDF). 2025年6月20日閲覧.
- ^ Schmidhuber, Jürgen (1991). “A possibility for implementing curiosity and boredom in model-building neural controllers”. Proc. SAB'1991. MIT Press/Bradford Books. pp. 222–227.
- ^ Schmidhuber, Jürgen (2020). “Generative Adversarial Networks are Special Cases of Artificial Curiosity (1990) and also Closely Related to Predictability Minimization (1991)” (英語). Neural Networks 127: 58–66. arXiv:1906.04493. doi:10.1016/j.neunet.2020.04.008. PMID 32334341.
- ^ Karras, T.; Aila, T.; Laine, S.; Lehtinen, J. (26 February 2018). “Progressive Growing of GANs for Improved Quality, Stability, and Variation”. arXiv:1710.10196 [cs.NE].
- ^ “GAN 2.0: NVIDIA's Hyperrealistic Face Generator”. SyncedReview.com (2018年12月14日). 2024年9月12日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ “Prepare, Don't Panic: Synthetic Media and Deepfakes”. witness.org. 2020年12月2日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ Sohl-Dickstein, Jascha; Weiss, Eric; Maheswaranathan, Niru; Ganguli, Surya (1 June 2015). “Deep Unsupervised Learning using Nonequilibrium Thermodynamics” (英語). Proceedings of the 32nd International Conference on Machine Learning (PMLR) 37: 2256–2265. arXiv:1503.03585. オリジナルの2024-09-21時点におけるアーカイブ。 2025年6月20日閲覧。.
- ^ Simonyan, Karen; Zisserman, Andrew (10 April 2015), Very Deep Convolutional Networks for Large-Scale Image Recognition, arXiv:1409.1556
- ^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). “Delving Deep into Rectifiers: Surpassing Human-Level Performance on ImageNet Classification”. arXiv:1502.01852 [cs.CV].
- ^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (10 December 2015). Deep Residual Learning for Image Recognition. arXiv:1512.03385.
- ^ Srivastava, Rupesh Kumar; Greff, Klaus; Schmidhuber, Jürgen (2 May 2015). “Highway Networks”. arXiv:1505.00387 [cs.LG].
- ^ He, Kaiming; Zhang, Xiangyu; Ren, Shaoqing; Sun, Jian (2016). “Deep Residual Learning for Image Recognition”. 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). IEEE. pp. 770–778. arXiv:1512.03385. doi:10.1109/CVPR.2016.90. ISBN 978-1-4673-8851-1. オリジナルの2024-10-07時点におけるアーカイブ。 2025年6月20日閲覧。
- ^ Linn, Allison (2015年12月10日). “Microsoft researchers win ImageNet computer vision challenge” (英語). The AI Blog. 2023年5月21日時点のオリジナルよりアーカイブ。2025年6月20日閲覧。
- ^ Sutskever, Ilya; Vinyals, Oriol; Le, Quoc Viet (2014). “Sequence to sequence learning with neural networks”. arXiv:1409.3215 [cs.CL].
- ^ Cho, Kyunghyun; van Merrienboer, Bart; Gulcehre, Caglar; Bahdanau, Dzmitry; Bougares, Fethi; Schwenk, Holger; Bengio, Yoshua (3 June 2014). “Learning Phrase Representations using RNN Encoder-Decoder for Statistical Machine Translation”. arXiv:1406.1078 [cs.CL].
- ^ a b c Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N.; Kaiser, Lukasz; Polosukhin, Illia (12 June 2017). “Attention Is All You Need”. arXiv:1706.03762 [cs.CL].
- ^ Schmidhuber, Jürgen (1992). “Learning to control fast-weight memories: an alternative to recurrent nets.”. Neural Computation 4 (1): 131–139. doi:10.1162/neco.1992.4.1.131.
- ^ Katharopoulos, Angelos; Vyas, Apoorv; Pappas, Nikolaos; Fleuret, François (2020). “Transformers are RNNs: Fast autoregressive Transformers with linear attention”. ICML 2020. PMLR. pp. 5156–5165. 2023年7月11日時点のオリジナルよりアーカイブ. 2025年6月20日閲覧.
- ^ Schlag, Imanol; Irie, Kazuki; Schmidhuber, Jürgen (2021). “Linear Transformers Are Secretly Fast Weight Programmers”. ICML 2021. Springer. pp. 9355–9366.
- ^ Wolf, Thomas; Debut, Lysandre; Sanh, Victor; Chaumond, Julien; Delangue, Clement; Moi, Anthony; Cistac, Pierric; Rault, Tim et al. (2020). “Transformers: State-of-the-Art Natural Language Processing”. Proceedings of the 2020 Conference on Empirical Methods in Natural Language Processing: System Demonstrations. pp. 38–45. doi:10.18653/v1/2020.emnlp-demos.6
- ^ a b c 渡邉正峰「意識の宿る機械をつくる ─甘利俊一の取り損ねたノーベル賞と今後の課題─」『科学哲学』第57巻第2号、2024年、13-20頁。
- ^ 石川眞澄「コネクショニズムと学習」『認知科学の発展』第4巻、1991年、51-77頁。
- ^ Homma, Toshiteru; Les Atlas; Robert Marks II (1988). “An Artificial Neural Network for Spatio-Temporal Bipolar Patters: Application to Phoneme Classification”. Advances in Neural Information Processing Systems 1: 31–40.
- ^ Yann Le Cun (June 1989). Generalization and Network Design Strategies.
- ^ Y. LeCun; B. Boser; J. S. Denker; D. Henderson; R. E. Howard; W. Hubbard; L. D. Jackel (1989). “Backpropagation applied to handwritten zip code recognition”. Neural Computation 1 (4): 541-551.
- ^ 植木一也「映像検索におけるディープラーニング」『日本神経回路学会誌』第24巻第1号、2017年、13-26頁。
- ^ 中原龍一「人工知能の歩み」『岡山医学会雑誌』第132巻第3号、2020年、144-147頁。
- ^ "A nonrecurrent network has no cycles. Nonrecurrent networks can be thought of as computing an input-output function." Jordan, M.I. (1986). Serial order: A parallel distributed processing approach. (Tech. Rep. No. 8604). San Diego: University of California, Institute for Cognitive Science.
- ^ a b c Vaswani et al. 2017, p. 6001.
- ^ Yu, Yong; Si, Xiaosheng; Hu, Changhua; Zhang, Jianxun (2019-07-01). “A Review of Recurrent Neural Networks: LSTM Cells and Network Architectures”. Neural Computation 31 (7): 1235–1270. doi:10.1162/neco_a_01199. ISSN 0899-7667.
- ^ Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N.; Kaiser, Lukasz; Polosukhin, Illia (2017-12-05). “Attention Is All You Need”. arXiv:1706.03762 [cs].
- ^ Neuromorphic Processing : A New Frontier in Scaling Computer Architecture Qualcomm 2014年
- ^ Qualcomm’s cognitive compute processors are coming to Snapdragon 820 ExtremeTech 2015年3月2日
- ^ a b c 複素ニューラルネットワーク
- ^ Akira Hirose, Shotaro Yoshida (2012). “Generalization Characteristics of Complex-valued Feedforward Neural Networks in Relation to Signal Coherence”. IEEE TNNLS 23 (4): 541-551.
- ^ 村田剛志『グラフニューラルネットワーク ― Pytorchによる実装』オーム社、2022年、 ISBN 978-4-274-22887-2。
- ^ The proposed U-Net based architecture allows to provide detailed per-pixel feedback to the generator while maintaining the global coherence of synthesized images
- ^ starting from a low resolution, we add new layers that model increasingly fine details as training progresses. This both speeds the training up and greatly stabilizes it PGGAN paper
- ^ "making normalization a part of the model architecture and performing the normalization for each training mini-batch." Sergey Ioffe, et. al.. (2015)
- ^ "ニューラルネットワークの演算の基本は、多入力の積和演算である。" 百瀬 (2016). 第2章:ディープ・ニューラルネットワークのニューロチップへの実装~その勘所は!!. semiconportal.
- ^ "深層学習の…フレームワーク中では, 計算時間の多くが畳み込み計算などの密行列積に費やされており … 計算時間の約90%が畳み込み層での計算時間であることが知られている" p.1 of 関谷, et al. (2017). 低ランク近似を用いた深層学習の行列積の高速化. 情報処理学会研究報告. Vol2017-HPC-158, No.24.
- ^ Optimize and Accelerate Machine Learning Inferencing and Training. ONNX Runtime.
- ^ "Direct Machine Learning (DirectML) is a low-level API for machine learning." Direct Machine Learning (DirectML). Microsoft.
- ^ "TensorRT can optimize and deploy applications to the data center, as well as embedded and automotive environments. It powers key NVIDIA solutions" NVIDIA TensorRT. NVIDIA.
- ^ "Quantization works by reducing the precision of the numbers used to represent a model's parameters, which by default are 32-bit floating point numbers." Model optimization. TensorFlow.
- ^ "Quantizing a network means converting it to use a reduced precision integer representation for the weights and/or activations." DYNAMIC QUANTIZATION. PyTorch.
- ^ "Quantization performance gain comes in 2 part: instruction and cache." Quantize ONNX Models. ONNX Runtime.
- ^ "Less memory usage: Smaller models use less RAM when they are run, which frees up memory for other parts of your application to use, and can translate to better performance and stability." Model optimization. TensorFlow.
- ^ "Old hardware doesn’t have or has few instruction support for byte computation. And quantization has overhead (quantize and dequantize), so it is not rare to get worse performance on old devices." Quantize ONNX Models. ONNX Runtime.
- ^ "Performance improvement depends on your model and hardware." Quantize ONNX Models. ONNX Runtime.
- ^ "Static quantization quantizes the weights and activations of the model. ... It requires calibration with a representative dataset to determine optimal quantization parameters for activations." QUANTIZATION. PyTorch.
- ^ "with dynamic quantization ... determine the scale factor for activations dynamically based on the data range observed at runtime." DYNAMIC QUANTIZATION. PyTorch.
- ^ "The model parameters ... are converted ahead of time and stored in INT8 form." DYNAMIC QUANTIZATION. PyTorch.
- ^ "Simulate the quantize and dequantize operations in training time." FAKEQUANTIZE. PyTorch. 2022-03-15閲覧.
- ^ "There are 2 ways to represent quantized ONNX models: ... Tensor Oriented, aka Quantize and DeQuantize (QDQ)." Quantize ONNX Models. ONNX RUNTIME. 2022-03-15閲覧.
参考文献
 |
出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。
|
- 上坂吉則『ニューロコンピューティングの数学的基礎』 近代科学社、1993年、 ISBN 4-7649-0219-2。
- 斎藤康毅『ゼロから作るDeep Learning - Pythonで学ぶディープラーニングの理論と実装』 オライリージャパン、2016年(第1刷)、 ISBN 978-4873117584。
- Vaswani, Ashish; Shazeer, Noam; Parmar, Niki; Uszkoreit, Jakob; Jones, Llion; Gomez, Aidan N.; Kaiser, Łukasz; Polosukhin, Illia (2017-12-04). “Attention is all you need”. Proceedings of the 31st International Conference on Neural Information Processing Systems (Red Hook, NY, USA: Curran Associates Inc.): 6000–6010. doi:10.5555/3295222.3295349. ISBN 978-1-5108-6096-4.
- 山内康一郎『作って学ぶニューラルネットワーク ― 機械学習の基礎から追加学習まで』 コロナ社、2020年、 ISBN 978-4-339-02911-6。
関連項目
- 人工知能
- 強化学習
- 機械学習
- ニューロコンピュータ
- コネクショニズム
- 認知科学
- ウォーレン・マカロック
- ウォルター・ピッツ
- ヘッブの法則
- 認知アーキテクチャ
- 階層構造
- 創発
- Neuroevolution
- コネクトーム
- ディープラーニング
- ヒトの脳
- 幹細胞
- 脳オルガノイド
外部リンク
- 『ニューラルネットワークモデル』 - コトバンク
- 『ニューラルネットワーク』 - コトバンク
ニューラルネットワーク (曖昧さ回避)
(Neural network から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/12/09 22:15 UTC 版)
ニューラルネットワークは、動物、人間、およびコンピューティング・システムにおける神経系の構造とアーキテクチャを形成する、相互接続されたニューロンの個体群またはニューロン・シミュレーションを指す:
- 生物学的ニューラルネットワーク(別名: 神経回路)、特定の機能を一緒に担う物理的に相互接続されたニューロンの集合
- 脳の大規模ネットワーク(Large scale brain networks)、より大規模な生物学的ニューラルネットワーク(i.e.、複数の神経回路の相互作用)
- 人工ニューラルネットワーク:ANN、動物の脳に見られる生物学的ニューラルネットワークにヒントを得たコンピューティング・システム
- 深層ニューラルネットワーク:DNN or ディープ・ニューラルネットワークとも、入力層と出力層の間に複数の層がある人工ニューラルネットワーク
- 畳み込みニューラルネットワーク:CNN、ディープ・ニューラルネットワークの一種で、たいてい一般的には視覚画像の分析に適用される
- 深層ニューラルネットワーク:DNN or ディープ・ニューラルネットワークとも、入力層と出力層の間に複数の層がある人工ニューラルネットワーク
Neural networks(ニューラル・ネットワークス)は以下を指すこともある:
- ニューラル・ネットワークス (学術誌)、査読済み科学学術誌
関連項目
- ニュートラル・ネットワーク (進化学)
- Gato (DeepMind) – これを書いている時にニューラルネットワークの国際言語間リンクがおかしいことに気付いたので
- Neural networkのページへのリンク





