ニューラルネットワーク
【英】：neural network
概要
(2) 神経回路の構造やニューロン(neuron)の作用を部分的に模倣した, コンピュータや電子回路を用いた人工的な「神経回路網」で, 記憶, 認識, 連想などの機能を実現する工学的なシステムのこと. ノイズに対する頑健性(robustness), 類似入力に対する汎化性(generalization), 学習が容易な高い適応性(adaptability), 並列処理への潜在的可能性をもつ.
詳説
ニューラルネットワーク (neural network) は神経回路網のことであり, その機能をコンピュータや専用ハードウェアで模倣したものを人工ニューラルネットワーク (artificial neural network) という. ORなどの分野で単にニューラルネットワークという場合は, 多くは人工ニューラルネットワークのことを指し, 具体的には比較的単純な非線形信号処理ユニットを結合することで構成されるネットワークのことと考えることが多い. ニューラルネットワークは本質的に並列分散処理的であり, 自己組織的であるといった特徴を内包している.
ニューラルネットワークの歴史を概観すると以下のようになる. 1943年にマッカロック（W. McCulloch）とピッツ（W. Pitts） [1] によるしきい値素子モデルが提案された. 1949年の心理学者D. Hebbの "The Organization of Behavior" [2] において示されたシナプス強化則とも言われる学習方法に関する考え方は, その後提案された多くのニューラルネットの学習方法の基礎となっている. 1962年, ローゼンブラット（F. Rosenblatt）によるパーセプトロン [3] (perceptron) が提案されたが, 1969年, ミンスキー（M. Minsky）とパパート（S. Papert）によるパーセプトロンの限界の呈示, 何人かの研究者による初期バージョンの後, 1986年にラメルハート（D. Rumelhart）, ヒントン（G. Hinton）, ウイリアムス（R. Williams）によりまとめられた階層型ニューラルネットワークの誤差逆伝播法 (back propagation) の定式化 [4] などを経て, 近年は, 脳の機能の実現を強く意識した研究も盛んに行われている.
ニューラルネットワークは2つの側面から最適化と関係が深い. まず1つは, ニューラルネットワークの機能としての最適化, もう1つは, 何らかの機能を実現するためのニューラルネットワークの学習における最適化である.
ホップフィールドネットワーク [5] (Hopfield network) は, 連想記憶を行ったり巡回セールスマン問題などの最適化問題を解くために考え出されたニューラルネットワークで, 1982年, ホップフィールド (J. J. Hopfield) により提案された. 記憶したいパターン情報は定係数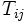
の中に埋めこまれる. このモデルは1984年, 連続値モデルに拡張された. 離散および連続モデルを合わせてホップフィールドネットワークと呼ばれる. ホップフィールドとタンク(T. W. Tank)は1985年に, ホップフィールドネットワークを巡回セールスマン問題の解法に用いる方法を示し [6] , ニューラルネットワークの最適化への応用の道を開いた.
ニューラルネットワークによる学習は, 教師あり学習, 教師なし学習に大別される. 教師あり学習とは, サンプルデータにおいて, 入力値に対して出力値が与えられ, 多数の入出力組の関係を同時に実現するようにモデルの中のパラメータを調整するモデルであり, その用途としては, 分類及び非線形回帰がある. この２つの本質的な違いは教師出力信号として2値信号を用いるか実数値を用いるかという点である. パーセプトロン, 階層型ネットワーク, RBF (radial basis function) ネットワークなどがあり, データのクラス判定や非線形関数近似を行うモデルを, 例 (examples) としてのデータから構築する. しきい値関数を使ったモデルでは, パーセプトロンなどのように, 誤り訂正学習が用いられる. また, ロジスティック (logistic) 関数などの微分可能関数を用いたモデルでは, 二乗誤差を最小化するような評価関数が学習に用いられる. 階層型ニューラルネットに二乗誤差最小化を取り入れると, 誤差逆伝播法が導かれる. 教師なし学習とは, 入力ベクトルだけがあるもので, 入力ベクトルに関する分布の情報を学習するものであり, 情報圧縮, 確率密度関数モデルを用いた推論などに応用される. コホネン（T. Kohonen）の自己組織化マップ (self organizing map), ガウス混合モデル (Gaussian mixture model), k-meansクラスタリングなどが代表的な例である.
人工知能においては, 記号論理をベースにしたシンボリストモデル (symbolist model) に対し, ニューラルネットワークの相互結合をもじったコネクショニストモデル (connectionist model) は, 相互に対極にあるものとして対比されてきた. シンボリストモデルは論理的な説明に適しており, コネクショニストモデルは学習が容易であるという特長を持つ反面, 一般にシンボリストモデルは学習が困難であり, コネクショニストモデルは説明能力に欠けるということがいえる. コネクショニストモデルが説明能力に欠けるというのは, 入力空間を自在に切り分けることができるがゆえにその複雑な切り口を言語的に説明することが困難なためであり, 欠点というよりもそのモデルの持つ特質からくる特徴であって, 特に言語的な説明を要しない制御などの分野では明らかに優れた能力を発揮する. また, 日々の売上データから顧客の特徴を抽出したり, クレジットカードの入会審査を行ったりするデータマイニング（data mining）の分野においても有力な手法として注目されている.
[1] W. W. McCulloch and W. Pitts, "A Logical Calculus of the Ideas Immanent in Nervous Activity," Bull. Math. Biophysics, 5 (1943), 115-133.
[2] A. O. Hebb, The Organization of Behavior, Wiley, 1949. 白井 訳, 『行動の機構』, 岩波書店, 1957.
[3] F. Rosenblatt, Principles of Neurodynamics, Spartan, 1962.
[4] D. E. Rumelhart, G. E. Hinton and R. J. Williams, "Learning Internal Representation by Error Propagation", in D. E. Rumelhart, J. L. McClelland and the PDP Research Group, Parallel Distributed Processing: Explorations in the Microstructure of Cognition, 1, Foundations, MIT Press, 1986. 甘利（監訳）, 『PDPモデル-認知科学とニューロン回路網の探索-』, 産業図書, 1989.
[5] J. J. Hopfield, "Neural Networks and Physical Systems with Emergent Collective Computational Abilities," in Proceedings of the National Academy of Sciences U.S.A., 79, 2554-2558, 1982.
[6] J. J. Hopfield and T. W. Tank, "Neural Computation of Decisions in Optimization Problems," Biological Cybernetics, 52 (1985), 141-152.
| 近似・知能・感覚的手法： | デンプスター・シェファーの証拠理論 データマイニング ナップサック問題 ニューラルネットワーク ニューラルネットワークによる学習 ファジィランダム変数 ファジィ推論 |
- にゅーらるねっとわーくのページへのリンク
