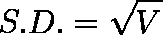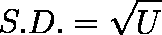ひょうじゅん‐へんさ〔ヘウジユン‐〕【標準偏差】
標準偏差(S.D.)
標準偏差
標準偏差
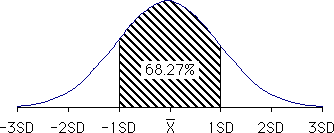
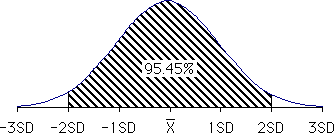
同じ測定を繰り返し、そのデータの分布をプロットすると、多くの場合正規分布曲線に従う。この分布曲線は、中心となる中心値と分布の大きさ(カーブの幅広さ)の2つのパラメータで定義される。 この分布が幅広ければ値のばらつきが大きく、狭ければばらつきが小さい。このバラつきの程度を数値化したものが標準偏差(standard deviation)と呼ばれる。
定義
ばらつきの程度を数値化するためは、測定値と平均値の差をとっていけばいいが、単純算術平均をそのままとると、正負の符号で値がキャンセルされてしまう。そこで、測定値と平均値の差の二乗(偏差平方和)をもとめ、その総和を得る。この総和をデータ数で割ることによって、分散が得られる。
分散
(m:平均値)
<m>sigma^2~=~sum{}{n}{(x_i-m)^2}/n</m>
例
<m 12>SD~=~sqrt{(109-134.75)^2+(98-134.75)^2+(140-134.75)^2+(192-134.75)^2}/4~=~36.46</m>
Excelで計算するには、データを母集団とみなす場合はSTDEVP、データを確率標本とみなす場合はSTDEV関数を使います。

CC Attribution-Noncommercial-Share Alike 3.0 Unported
標準偏差
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/04/09 15:01 UTC 版)


標準偏差を2乗したのが分散であり、従って、標準偏差は分散の非負の平方根である[1]。標準偏差が 0 であることは、データの値が全て等しいことと同値である。
母集団や確率変数の標準偏差を σ で、標本の標準偏差を s で表すことがある。
二乗平均平方根 (RMS) を用いると、標準偏差は偏差の二乗平均平方根に等しくなる。
概要
データ x1, x2, …, xn の平均値からの散らばり具合を数値にした標準偏差は、次の式で定義される:
-

z → p 
p → z 信頼区間 信頼度 不信頼度 百分率 百分率 分数 0.318639σ 25% 75% 3/4 0.674490σ 50% 50% 1/2 0.994458σ 68% 32% 1/3.125 1σ 68.2689492% 31.7310508% 1/3.1514872 1.281552σ 80% 20% 1/5 1.644854σ 90% 10% 1/10 1.959964σ 95% 5% 1/20 2σ 95.4499736% 4.5500264% 1/21.977895 2.575829σ 99% 1% 1/100 3σ 99.7300204% 0.2699796% 1/370.398 3.290527σ 99.9% 0.1% 1/1000 3.890592σ 99.99% 0.01% 1/10000 4σ 99.993666% 0.006334% 1/15787 4.417173σ 99.999% 0.001% 1/100000 4.5σ 99.9993204653751% 0.0006795346249% 1/147159.5358 = 3.4/1000000 4.891638σ 99.9999% 0.0001% 1/1000000 5σ 99.9999426697% 0.0000573303% 1/1744278 5.326724σ 99.99999% 0.00001% 1/10000000 5.730729σ 99.999999% 0.000001% 1/100000000 6σ 99.9999998027% 0.0000001973% 1/506797346 6.109410σ 99.9999999% 0.0000001% 1/1000000000 6.466951σ 99.99999999% 0.00000001% 1/10000000000 6.806502σ 99.999999999% 0.000000001% 1/100000000000 7σ 99.9999999997440% 0.000000000256% 1/390682215445 脚注
注釈
- ^ 極端な例として、標本の大きさが 1 の場合、ばらつきがないので標本の分散は必ず 0 となるが、母集団のばらつきは通常 0 ではない。
出典
- ^ JIS Z 8101-1:1999, 1.13 分散.
- ^ a b 高校からの統計・データサイエンス活用 総務省政策統括官(統計基準担当)p.34
- ^ 平均への回帰、相関係数―統計学史(2) ブログ 統計WEB
- ^ 農環研ウェブ高座 「農業環境のための統計学」 第10回 (農業と環境 No.158 2013.6)
- ^ 酒井弘憲「第5回 統計学の巨人:ゴルトンとピアソン」『ファルマシア』第52巻第2号、日本薬学会、2016年、164-165頁、doi:10.14894/faruawpsj.52.2_164、ISSN 0014-8601、 NAID 130005127751。
- ^ カール ピアソンとは - コトバンク
- ^ 【科学史の肖像】Karl Pearson, 1857-1936
- ^ 標準偏差の名付け親は,相関係数で有名なピアソン,不偏標準偏差の話題と共に 生物科学研究所 井口研究室
- ^ 分散投資の意義② 投資のリスクとは|年金積立金管理運用独立行政法人
- ^ 標準偏差・分散|証券用語解説集|野村證券
- ^ a b 栗原 2011, p. 47
- ^ 稲垣 1990, p. 21.
- ^ 吉澤 1989, pp. 78–79.
- ^ Brugger 1969, p. 32.
- ^ 例:(東京大学教養学部統計学教室編 1991)。
- ^ 分散または標準偏差の図による解説と具体例は、(村瀬, 高田 & 廣瀬 2007, pp. 52–53)などを参照。
- ^ “Earliest Known Uses of Some of the Words of Mathematics (S)”. 2016年1月30日閲覧。
- ^ 「Estimating Parameters Web Page」
- ^ 「健康統計学-散布度」
- ^ 「高崎経済大学非常勤講義 第4回「記述統計(2):代表値」」
- ^ 「標準偏差の不偏性」
参考文献
- Brugger, Richard M (1969-10). “A Note on Unbiased Estimation of the Standard Deviation”. The American statistician (ASA(アメリカ統計学会)) 23 (4): 32. doi:10.1080/00031305.1969.10481865. ISSN 0003-1305.
- 吉澤康和『新しい誤差論 - 実験データ解析法』共立出版、1989年。 ISBN 4320014243。
- 稲垣宣生『数理統計学』裳華房、1990年。 ISBN 4-7853-1406-0。
- 『統計学入門』東京大学出版会、1991年。 ISBN 4-13-042065-8。
- 村瀬洋一、高田洋、廣瀬毅士『SPSSによる多変量解析』オーム社、2007年。 ISBN 4-27-406626-6。
- 栗原伸一『入門統計学検定から多変量解析・実験計画法まで』オーム社、2011年。 ISBN 978-4-274-06855-3。
- 西岡康夫『数学チュートリアル やさしく語る 確率統計』オーム社、2013年。 ISBN 9784274214073。
- 伏見康治『確率論及統計論』河出書房、1942年。 ISBN 9784874720127。
- 日本数学会 編『数学辞典』岩波書店、2007年。 ISBN 9784000803090。
- 日本規格協会, JIS Z 8101-1:2015 統計−用語及び記号−第1部:一般統計用語及び確率で用いられる用語
関連項目
外部リンク
- Weisstein, Eric W. "Standard Deviation". mathworld.wolfram.com (英語).
- 『標準偏差』 - コトバンク
標準偏差
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/12/24 05:46 UTC 版)
詳細は「標準偏差」を参照 データの標準偏差とは、元のデータの値たちを、平均値を変えず絶対偏差を一定値 s に取り直したとき(データの大きさが奇数のときは同じデータを併せて偶数にする)、2つの偏差ベクトルのユークリッドノルムが等しくなるような s のこと。データの偏差の自乗の平均の平方根(非負)に等しくなる。標準偏差は偏差の一部ではない。値が全て有理数でも標準偏差は平均偏差と違い無理数になることが多い。標準偏差は常に平均偏差以上になる。
※この「標準偏差」の解説は、「偏差」の解説の一部です。
「標準偏差」を含む「偏差」の記事については、「偏差」の概要を参照ください。
標準偏差
「標準偏差」の例文・使い方・用例・文例
標準偏差と同じ種類の言葉
「標準偏差」に関係したコラム
-
FXやCFDの標準偏差チャネルとは、線形回帰線から一定の標準偏差分を乖離した直線のことです。標準偏差チャネルは、線形回帰線からプラスに乖離した直線と、マイナスに乖離した直線の2本の線を描画します。下の...
-
FX(外国為替証拠金取引)のボリンジャーバンド(略称、ボリバン)とは、現在の為替レートが高値圏にあるか安値圏にあるかを判断するためのテクニカル指標です。また、ボリンジャーバンドはトレンドの転換点を見つ...
-
株式分析のヒストリカル・ボラティリティ(Historical Volatility)とは、過去の株価のデータから、将来の株価の変動率を求めるテクニカル指標のことです。ヒストリカル・ボラティリティは、H...
FXのチャート分析ソフトMT4のStandard Deviationの見方
FX(外国為替証拠金取引)のチャート分析ソフトMT4(Meta Trader 4)のStandard Deviationの見方について解説します。Standard Deviationは、過去の為替レー...
- 標準偏差のページへのリンク