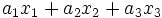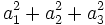多変量解析
多変量解析 multi-variate analysis
多変量解析
複数の特性値に対してデータの特徴を要約し、目的に応じたデータの統合化を行う手法。いろいろな手法があるが、主成分解析がもっともよく知られている。多くの因子のなかから要因となるものを知ることができる。
多変量解析
【英】：multivariate analysis
概要
解析の対象に対して, 複数の変数(特性)についての値が得られているときに, それらを用いて, 総合的に解析するのを多変量解析という. 変数の型および変数の扱い方により, 種々の解析方法がある. 主成分分析や因子分析のように, すべての変数を同じに扱う場合と, 回帰分析のように, 変数を2つのグループに分けて, 一方で他方を説明する場合がある.
詳説
解析の対象 (会社, 地域, 人など) に対して, 複数の変数 (特性) についての値が得られているときに, それらを用いて, 総合的に解析するのを多変量解析という. 変数の型および変数の扱い方により, 種々の解析方法がある.
変数の型は, 同異だけがわかる名義尺度変数 (質的変数) と差に意味がある間隔尺度変数 (量的変数) に分かれる. 会社名, 地名, 人名などは, 名義尺度変数である. 名義尺度変数は, 分類にしか使えないが, 複数の間隔尺度変数は, 重み(係数)を乗じて, 加えた関数を考えることができる.
変数の扱い方には, すべての変数を同じに扱う場合と二つに分ける場合がある. 後者では, 第1のグループの変数の関数と第2のグループの変数の対応を求める. 第1のグループの変数を説明変数, 第2のグループの変数を目的変数という. 目的変数は, 1個であることが多い.
すべての変数が名義尺度変数である場合は, 対象を多重に分類した分割表を解析する方法があるが, 通常は, 多変量解析の対象にしていないので, ここでは, すべての変数が間隔尺度変数であるとする.
元の変数との関係をできるだけ失わないようにして, より少数の総合特性値をいくつか求める方法として, 主成分分析や因子分析がある. 主成分分析では, 主成分といわれる元の変数の線形式を順次一つずつ求めていく. したがって, 第
(≧2)主成分には, すでに定まっている第1から第
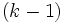主成分までに追加するのに最適なものが選ばれる. しかし, とりあげる総合特性値の数が予め定まっている場合は, 第1主成分から第主成分の1次変換であれば, どれでもよいので, 意味を考えて, よりよい個の因子と呼ばれる総合特性値を求めるのが因子分析である.
対象をいくつかのグループに分類する方法として, クラスター分析がある.
説明変数は, すべて間隔尺度変数であるとする. 目的変数との関係がある説明変数の関数を求める方法がいくつか考えられている.
目的変数によって対象をグループ分けしたとき, 同じグループ内では近い値をとり, 異なるグループでは離れた値をとる説明変数の関数が求められれば, 説明変数で目的変数を判別することができる. 目的変数を判別するために用いる説明変数の関数を判別関数という.
その値が目的変数の値とできるだけ近くなるような説明変数の関数を求める方法として, 回帰分析がある.
ある特徴の有無, 質問の肯定・否定による回答などのように, 二つに分けられる名義尺度変数は, 0か1の値をとる0-1変数におきかえることで, 間隔尺度変数のように扱うことができる. 一般に, 個に分ける名義尺度変数は, 個の0-1変数に置き換えることができる.
0-1変数だけの多変量解析として, 各種の数量化法が提案されている.
順序だけ意味がある順序尺度変数は, 点数化によって, 間隔尺度変数にできる. たとえば, 品物に松, 竹, 梅のランクが付けられている場合, それぞれに, 3, 2, 1や5, 2, 1の数値を対応させれば, 間隔尺度変数として扱うことができる. なお, 順序尺度変数は, 順位相関係数を用いて, 解析することもできる.
比が意味を持つ比尺度変数は, その対数をとることによって, 間隔尺度変数になる.
複数の変数を扱うとき, 単位に注意する必要がある. 単位がすべて同じであれば, ほとんど問題がないが,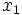 
の単位はm, 
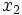はcm,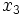 
はgのように, 異なるときは, 重み (係数) 
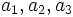の単位を変えることによって, 重み付きの和
多変量解析では, 単位を揃えることとばらつきを揃えることを兼ねて, 初めにその変数の標準偏差で割る変数変換がよく行われる.
多変量解析
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2025/02/16 18:18 UTC 版)
 | この項目「多変量解析」は加筆依頼に出されており、内容をより充実させるために次の点に関する加筆が求められています。 加筆の要点 - 統計学の分野の内容をベースとした導入部分の出典明記・加筆など。また、各学問での多変量解析の利用など。 （貼付後はWikipedia:加筆依頼のページに依頼内容を記述してください。記述が無いとタグは除去されます） （2020年7月） |
多変量解析（たへんりょうかいせき、英語: multivariate analysis）は、多変量のデータの特徴を要約する方法のことである[1]。データの要約により、データの特徴を単純化し、分析しやすくする[2]。
当初は統計学の理論として生まれたが、コンピュータの発展とともに他の分野でも応用されるようになっていった[1]。
主な多変量解析
 | この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 (2011年11月) |
各分野での利用
 | この節の加筆が望まれています。 |
人文地理学
人文地理学では、地域分析において多変量解析が重要な手法となる[3]。1950年代後半以降、計量地理学の理論を構築していくうえで多変量解析が利用されていった[4]。人文地理学では、重回帰分析による地域間の連結性の把握、主成分分析による都市の内部構造の分析、因子分析・クラスター分析による因子生態分析や等質地域・機能地域の地域区分などが行われる[5]。
地域分析で多変量解析を行う場合は、まず地理行列を作成する[6]。等質地域の設定を行う場合は属性行列、機能地域の設定を行う場合は相互作用行列を作成し、多変量解析を行うことになる[7]。
脚注
- ^ a b 水野 1996, p. 1.
- ^ 水野 1996, p. 3.
- ^ 村山・駒木 2013, p. 19.
- ^ 村山・駒木 2013, p. 21.
- ^ 村山・駒木 2013, pp. 22–23.
- ^ 村山・駒木 2013, p. 22.
- ^ 村山・駒木 2013, p. 25.
参考文献
- 水野欽司『多変量データ解析講義』朝倉書店、1996年。ISBN 4-254-12548-8。
- 村山祐司、駒木伸比古『新版 地域分析』古今書院、2013年。ISBN 978-4-7722-5272-0。
教科書
- 小西貞則：「多変量解析入門：線形から非線形へ」、岩波書店、ISBN 978-4-00-005653-3 (2010年1月26日).
外部リンク
- 『多変量解析』 - コトバンク
- 多変量解析とは？入門者にも理解しやすい手順や具体…｜Udemy メディア
| 標本調査 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 記述統計学 |
| ||||||||||||||
| 推計統計学 |
| ||||||||||||||
| ベイズ統計学 |
| ||||||||||||||
| 相関 |
| ||||||||||||||
| モデル | |||||||||||||||
| 回帰 |
| ||||||||||||||
| 分類 |
| ||||||||||||||
| 教師なし学習 |
| ||||||||||||||
| 統計図表 | |||||||||||||||
| 生存時間分析 | |||||||||||||||
| 歴史 |
| ||||||||||||||
| 応用 | |||||||||||||||
| 出版物 |
| ||||||||||||||
| 全般 | |||||||||||||||
| その他 | |||||||||||||||
 カテゴリ | |||||||||||||||
 | この項目は、社会科学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（PJ:社会科学）。 |
 | この項目は、自然科学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（Portal:自然科学）。 |
多変量解析
出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/03/14 05:27 UTC 版)
多変量グレンジャー因果性検定は通常、ベクトル自己回帰モデル（VAR）を時系列データに当てはめて行われる。特に、時間 t = 1 , … , T {\displaystyle t=1,\ldots ,T} において X ( t ) ∈ R d × 1 {\displaystyle X(t)\in \mathbb {R} ^{d\times 1}} を d {\displaystyle d} 次元の多変量時系列とする。グレンジャー因果性は、 L {\displaystyle L} 個の時点に対するVARモデルで以下のように行われる。 X ( t ) = ∑ τ = 1 L A τ X ( t − τ ) + ε ( t ) , {\displaystyle X(t)=\sum _{\tau =1}^{L}A_{\tau }X(t-\tau )+\varepsilon (t),} ここで、 ε ( t ) {\displaystyle \varepsilon (t)} はホワイトガウスランダムベクトルであり、 A τ {\displaystyle A_{\tau }} はそれぞれの τ {\displaystyle \tau } における行列である。 τ = 1 , … , L {\displaystyle \tau =1,\ldots ,L} において要素 A τ ( j , i ) {\displaystyle A_{\tau }(j,i)} の１つ以上がゼロよりも（絶対値が）大幅に大きい場合には、時系列 X i {\displaystyle X_{i}} から別の時系列 X j {\displaystyle X_{j}} へグレンジャー因果性があるとされる。
※この「多変量解析」の解説は、「グレンジャー因果性」の解説の一部です。
「多変量解析」を含む「グレンジャー因果性」の記事については、「グレンジャー因果性」の概要を参照ください。
多変量解析と同じ種類の言葉
固有名詞の分類
- 多変量解析のページへのリンク
