母数
μ
∈
R
{\displaystyle \mu \in \mathbb {R} }
また、多変量の統計 として共分散 まで込めた多次元の正規分布も定義され、平均 μ = (μ 1 , μ 2 , …, μn )n 次元正規分布の同時密度関数は次の式で与えられる。
f
(
x
)
=
1
(
2
π
)
n
|
Σ
|
exp
(
−
1
2
(
x
−
μ
)
T
Σ
−
1
(
x
−
μ
)
)
{\displaystyle f(x)={\frac {1}{({\sqrt {2\pi }})^{n}{\sqrt {\vert {\mathit {\Sigma }}\vert }}}}\exp \!\left(-{\frac {1}{2}}(x-\mu )^{\mathrm {T} }\,{\mathit {\Sigma }}^{-1}(x-\mu )\right)}
歪正規分布の確率密度関数
正規分布の拡張としては、上で示した多次元化を施した多変量正規分布の他に、歪正規分布 (Skew-Normal (SN) distribution) がある。これは三変数で表現され、そのうち1つの変数について α = 0φ (x )
ϕ
(
x
)
=
1
2
π
e
−
x
2
2
{\displaystyle \phi (x)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {x^{2}}{2}}}}
ゴルトンボード では、1つの球が落ちる過程で二項分布に従う動きを繰り返し、正規分布に近づく。正規分布が統計学 上特別な地位を持つのは中心極限定理 独立同分布 に従う確率変数
X
{\displaystyle X}
正規Q-Qプロット
何らかの事象について法則性を捜したり理論を構築しようとしたりする際、その確率分布がまだ分かっていない場合にはそれが正規分布であると仮定して推論することは珍しくないが、誤った結論にたどりついてしまう可能性がある。標本データが正規分布に近似しているかどうを判断するためには、尖度 と歪度 を調べる、ヒストグラム を見る、正規Q-Qプロット をチェックする、あるいはシャピロ–ウィルク検定 やコルモゴロフ–スミルノフ検定 （正規分布）を利用する方法などが一般的に行われている。
平均や分散が未知の正規分布に従うデータから、母数 θ = (μ , σ 2 )
θ
^
=
(
μ
^
,
σ
^
2
)
{\displaystyle {\hat {\theta }}=({\hat {\mu }},{\hat {\sigma }}^{2})}
標準正規分布がもつ確率密度関数のグラフ
正規分布 N (μ , σ 2 )x を取ると、平均 μ からのずれが ±1σ 以下の範囲に x が含まれる確率は 68.27%、±2σ 以下だと 95.45%、さらに ±3σ だと 99.73% となる[ 1] 68–95–99.7則 と呼ばれることもある。
正規分布は、t分布 やF分布 といった種々の分布の考え方の基礎になっているだけでなく、実際の統計的推測 においても、仮説検定 、区間推定 など、様々な場面で利用される。
正規分布 N (μ , σ )X が与えられたとき Z = X − μ / σ Z は標準正規分布に従う。大学レベルの統計入門のクラスでは必ず行われているが、Z 値を求めることで標準正規分布表
不連続値をとる確率変数についての検定の場合でも、連続変数と同様の考え方で正規分布を近似的に用いることがある。これは標本の大きさ n が大きく、かつデータの階級幅が狭いほど、近似の精度が高い。
標準正規分布における信頼度の推移 標準正規分布におけるσ 区間の推移
信頼区間に対する信頼度の推移
信頼区間
信頼度
危険率
百分率
百分率
比
0.318 639σ
25% 75%
3 / 4
0.674490σ
50% 50%
1 / 2
0.994458σ
68% 32%
1 / 3.125
1σ 68.2689492%
31.7310508%
1 / 3.1514872
1.281552σ
80% 20%
1 / 5
1.644854σ
90% 10%
1 / 10
1.959964σ
95% 5%
1 / 20
2σ 95.4499736%
4.5500264%
1 / 21.977895
2.575829σ
99% 1%
1 / 100
3σ 99.7300204%
0.2699796%
1 / 370.398
3.290527σ
99.9%
0.1% 1 / 1000
3.890592σ
99.99%
0.01% 1 / 10000
4σ 99.993666%
0.006334%
1 / 15787
4.417173σ
99.999%
0.001% 1 / 10,0000
4.5σ
99.999320 465 3751% 0.0006795346249%
1 / 14,7159.5358
4.891638σ
99.9999%
0.0001% 1 / 100,0000
5σ 99.9999426697%
0.0000573303%
1 / 174,4278
5.326724σ
99.99999%
0.00001% 1 / 1000,0000
5.730729σ
99.999999%
0.000001% 1 / 1,0000,0000
6σ 99.9999998027%
0.0000001973%
1 / 5,0679,7346
6.109410σ
99.9999999%
0.0000001% 1 / 10,0000,0000
6.466951σ
99.99999999%
0.00000001% 1 / 100,0000,0000
6.806502σ
99.999999999%
0.000000001% 1 / 1000,0000,0000
7σ 99.9999999997440%
0.000000000256%
1 / 3906,8221,5445
引用元：(成実清松 & 坂井忠次 1952 )
標準正規分布
X
∼
N
(
0
,
1
)
{\displaystyle X\sim N(0,1)}
出典は列挙するだけでなく、脚注 などを用いてどの記述の情報源であるかを明記してください。 記事の信頼性向上にご協力をお願いいたします。（2016年4月 ） 
,
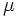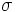を
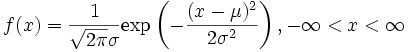
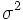となる. この
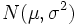という
カテゴリ
