最尤法

デジタル大辞泉

さいゆう‐ほう〔サイイウハフ〕【最^×尤法】

読み方：さいゆうほう

数理統計学で、与えられた観測値（標本）から、それらが得られる確率を最大化する確率分布の母数を推定する手法。最尤推定法。

統計学用語辞典

最尤法

　一致性，有効性，十分性を満たす最適推定量は，最尤法 により求めることができる。
　母数が θ である母集団 f ( x | θ ) から，n 個の標本 X1，X2，... ，Xn が抽出されたとする。
　このとき，確率密度は（1）式で表せる。
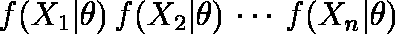　　……（1）
　今までは，母数 θ を持つ母集団から抽出された一つの確率変数 x が X という実現値をとるとして，f ( x | θ ) を x の関数と見てきたが，x が固定されていると考えれば （1）式は θ の関数とみなすこともできる。
　このとき，フィッシャーは（1）式を 尤度関数 と呼び，（2）式で定義される θ の取りうる種々の値に対する L を θ の 尤度 と定義した。
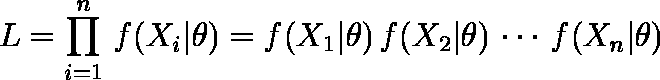　　……（2）
　最尤法とは，X1，X2，...，Xn を固定した場合に θ の尤度が最大になるように 最尤推定量 を求めることである。
　最尤推定量は（2）式を θ で微分すれば求めることができる。 しかし，実際の計算では L の対数をとった（3）式を用いる方が便利である。 L の最大値を与える を求めることは，（3）式の最大値を与える を求めることと同じである。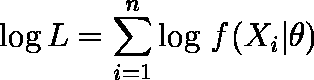
　　……（3）
　なお，（2）式の θ の最尤推定量を とおくと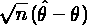， は，n → ∞ のとき漸近的に正規分布 に従う。ただし，I(θ) はフィッシャー情報量である。

生物学用語辞典

最尤法

英訳・(英)同義/類義語：maximum likelihood method, maximum likelihood approach

分子系統樹を作成する手法の一つで、系統樹ごとに塩基やアミノ酸の置換確率を計算し、確率的な可能性が最も高くなるような系統樹を作成する方法。

「生物学用語辞典」の他の用語

実験方法装置単位など：

放射線  暗視野顕微鏡  最大節約法  最尤法  最近隣法  有根系統樹  染色

ウィキペディア

最尤推定

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/03/20 23:22 UTC 版)

最尤推定（さいゆうすいてい、英: maximum likelihood estimationという）や最尤法（さいゆうほう、英: method of maximum likelihood）とは、統計学において、与えられたデータからそれが従う確率分布の母数を点推定する方法である。

ウィキペディア小見出し辞書

最尤法

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2020/11/13 07:51 UTC 版)

「Partial Response Maximum Likelihood」の記事における「最尤法」の解説

詳細は「ビタビアルゴリズム」を参照 最尤 ( ML ) 復号では、ビタビアルゴリズムを利用して、"1"、"0"の推定を行う。このビタビ復号器には、PR後 ( 波形等化後 ) の信号が入力される。 このMLでは、今しがた入力された信号に応じて即座にその"1"、"0"の判別を行うわけではなく、ある程度時系列的にまとまった複数のビットを観察した後、それらの尤度が最も高くなるように判別する特徴がある。 最尤復号とPR 4の組み合わせでは、以下の4つの磁化の状態を準備する: ( 1 1 )、( 1 0 )、( 0 1 )、( 0 0 ) 。( 1 0 )は現在の磁化の状態が0で、その直前が1であった事を意味する。PR 4では3値 ( -1, 0, 1 ) しか持たない事を説明したが、この3値の何れかを入力として受け取ると、状態間の遷移が起こることになる。ここで、現在の状態から次の状態に遷移するのに必要なPR 4の理想値は決まっている、という事が重要である。例えば、現在の状態が( 0 1 )の時、次に ( 1 1 )に遷移するには、PR 4の値として 1 を、( 1 0 )に遷移するには 0 が入力されねばならない。それと同時に許可されない遷移も定義され、例えば、( 0 1 ) から ( 0 0 ) 及び( 0 1 )には直接遷移し得ない。 これらを考慮すると、実際に入力されたPR 4の信号値と各理想値の差分を取れば、次にどの状態に遷移するのが確からしいのか、その尤度を定量化する事が出来る。これを時系列的に複数ビットで繰り返し、起こり得る遷移の「パス」毎にその尤度を積算していけば、最も確からしい遷移の一連のパスが最終的に見つかり得る。PRMLではこの生き残りのパスが見つかって初めて、"1"、"0"を判別する。