多重共線性 multicollinearity
詳しくは,重回帰分析を参照のこと。
多重共線性
変数選択を行わない場合には,独立変数相互間に相関の高いものは含めないほうがよい。
もし,それらの中に独立でないものが含まれていると( 例えば変数 A,B とその合計値 C = A + B が共に含まれていると )分析は失敗する。
場合によっては,各独立変数と従属変数との相関係数の符号と,偏回帰係数の符号が一致しない場合が生ずる。これは,「予測を行う」という観点から偏回帰係数が定められるので,重回帰式に含まれた変数相互間の関連で符号が決められるためである。このようなことが起きるのは,独立変数間に相関の高いものが混ざっていることが原因である( ある変数で予測しすぎた部分を別の変数で打消しているような場合がある )。しかし,このようなことは因果関係を考える上では不都合なので,符号が一致しない独立変数を除いた重回帰式を探索するとよいであろう。
独立変数間の相関係数行列の逆行列の要素を rii としたとき,
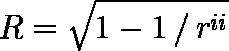
は,独立変数 i を残りの独立変数で予測するときの重相関係数になっている。したがって,この数値が大きいものは独立変数としてふさわしくないことを表す。
これと同じことであるが 1 / rii を トレランス,rii を 分散拡大係数 と呼ぶことがある。この場合には,トレランスが低い( 分散拡大係数が大きい )独立変数は除く方がよいことを表す。
多重共線性
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/03/24 09:45 UTC 版)

|
この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。(2021年6月)
|
統計学において、多重共線性(たじゅうきょうせんせい、英語: Multicollinearity、単に共線性とも略される)とは、重回帰モデルにおいて、説明変数の中に、相関係数が高い組み合わせがあることをいう(例: 体重とBMI)。重回帰分析の際、説明変数を増やすほど決定係数が高くなりやすいために、より多くの説明変数を入れ、多重共線性を起こす可能性がある[1]。このような状況では、モデルやデータの小さな変化に応じて、重回帰の係数推定値が不規則に変化しうる。多重共線性は、少なくともサンプルデータセット内では、全体としてのモデルの予測力または信頼性を低下させず、個々の予測変数に関する計算にのみ影響を与える。つまり、共線性予測変数を持つ多変量回帰モデルは、予測変数の全体がどれだけよく結果変数を予測するかを示すことができるが、個々の予測変数に関する有効な結果、またはどの予測変数が不要かに関しては有効な結果を与えないことも考えられる。
なお、最小二乗法(OLS)などの回帰分析の前提条件を説明する際、「多重共線性がない」という表現は、完全な多重共線性がないこと、すなわち予測変数間に正確な(非確率的な)線形関係がないことを意味する。このような場合、計画行列 
数学的には、ある変数の間に1つ以上の厳密な線形関係が存在する場合、その変数の集合は完全な多重共線性を持つ。例えば、次のような場合である。
-

この項目は、統計学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています(プロジェクト:数学/Portal:数学)。
多重共線性
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/03/27 14:50 UTC 版)
「多重共線性」も参照 独立変数(説明変数)を選択する際、マーケティングやアンケートでよく使う一般的な重回帰の場合、複数の説明変数同士は強い相関がないという仮定が入っている。そのため、説明変数同士が関連性の高い場合、一般化線形モデルでは多重共線性と呼ばれる状態になるため、係数が直感に反する値になることがある。 例えば、小学校での定期テスト得点から重回帰で分析する場合、理科の点数を従属変数に、数学と国語とを説明変数にした場合、数学が増えると理科の点数が増え、国語の点数が高ければ理科の点数が減るといった意味の係数が出ることがある。これは数学と国語との点数の間に強い相関がある(一般に、どちらの成績も学習習慣や知能の影響を強く受ける)ことで起こりうる。この場合のように説明変数間の相関が高いと係数が不安定になりやすい。 実務的対応としては、一方を除いて分析するのが最も手軽である。また、数学と国語の平均点と、数学と国語の得点の差というように和と差に数字を加工すると、この2つは相関がたいてい低く、かつ解釈しやすい。数学と国語の得点の差は、数学の方が高い生徒の方が理科の点数が高い傾向があるというように理解できるためである。ただし、このような正の相関を持つ変数同士の差得点は元の変数よりも信頼性が落ちるので、サンプル数を増やすなどの対応が求められる。 また、適切な予測力を実質的には持たない変数であっても、説明変数に加えると予測式自体の寄与率(決定係数)R2は上がることが多い。そのため、単なるR2ではなく、その分を調整した修正R2を参照する、ステップワイズ法(英語版)等で投入する説明変数を取捨選択する、AICを見るなどの対応が求められる。
※この「多重共線性」の解説は、「重回帰分析」の解説の一部です。
「多重共線性」を含む「重回帰分析」の記事については、「重回帰分析」の概要を参照ください。
多重共線性と同じ種類の言葉
- 多重共線性のページへのリンク
