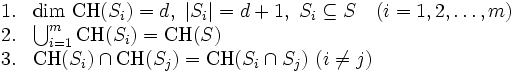三角測距
三角形分割
【英】:triangulation
概要
点集合の三角形分割とは, 2次元においてはその凸包を2-単体すなわち三角形に, 3次元では3--単体すなわち四面体に分割することである(四面体分割ともいう). 一般の次元の場合は単体分割あるいは簡単に三角形分割といわれる. 三角形分割は, 凸包・凸多面体とならんで基本的な幾何構造であり, 理論的に重要であるだけでなく, コンピュータグラフィクスや有限要素解析・内挿で のメッシュ生成など広く応用がある.
詳説
点集合の三角形分割(triangulation)とは, 2次元においてはその凸包を2-単体 すなわち三角形に, 3次元では3-単体すなわち四面体に分割した構造である(四面体分割ともいう). 一般の次元の場合は単体分割あるいは簡単に三角形分割といわれる. 三角形分割は, 凸包・凸多面体とならんで基本的な幾何構造であり, 理論的に 重要であるだけでなく, コンピューターグラフィクスや有限要素解析・内挿でのメッシュ生成など広く応用がある.
 を
を 次元の
次元の 点の集合,
点の集合, 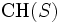 を
を の凸包とする.
の凸包とする.  の三角形分割
の三角形分割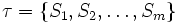 と は, 次の条件を満たすものである.
と は, 次の条件を満たすものである.
平面上の一般の位置にある点集合 と
と の点をすべて用いる三角形分割を考える.
の点をすべて用いる三角形分割を考える.  のどの三角形分割も, オイラー(L. Euler)の公式から同じ数の三角形をもつ. また, 三角形分割の個数については, 三角形分割の平面性に着目して解析することにより
のどの三角形分割も, オイラー(L. Euler)の公式から同じ数の三角形をもつ. また, 三角形分割の個数については, 三角形分割の平面性に着目して解析することにより 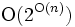 であることがいえる. 凸
であることがいえる. 凸 角形の頂点の場合は, 三角形分割の個数は
角形の頂点の場合は, 三角形分割の個数は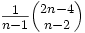 である. 動的計画法を用いることにより, 多角形内部の三角形分割の数を数える ことは多項式時間で行えるが, 一般の点集合の三角形分割の個数を多項式時間 で数えることができるかどうかは未解決の問題である. 多数の三角形分割の中から1つ選ぶ際の基準として代表的なものを上げる.
である. 動的計画法を用いることにより, 多角形内部の三角形分割の数を数える ことは多項式時間で行えるが, 一般の点集合の三角形分割の個数を多項式時間 で数えることができるかどうかは未解決の問題である. 多数の三角形分割の中から1つ選ぶ際の基準として代表的なものを上げる.
他にも色々な評価規準が考えられる. 以下で述べるドロネー三角形分割は, このうち最小角最大, 最大包含円最小という性質を満たし(最大外接円最小も), かつ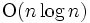 の高速の時間で求めることができる. 最大角を最小にする
の高速の時間で求めることができる. 最大角を最小にする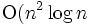 )時間の動的計画法を用いたアルゴリズム も知られている. 一方, 辺長和を最小にする重み最小三角形分割 問題の複雑さについてはまだよくわかっていないが, 2次元の場合は解法が与えられている. 点集合が凸
)時間の動的計画法を用いたアルゴリズム も知られている. 一方, 辺長和を最小にする重み最小三角形分割 問題の複雑さについてはまだよくわかっていないが, 2次元の場合は解法が与えられている. 点集合が凸 角形の頂点集合の場合, 辺長和最小問題は動的計画法によって
角形の頂点集合の場合, 辺長和最小問題は動的計画法によって 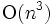 時間で解ける. アスベクト比最適化なども含めた整数計画によるアプローチも はかられている.
時間で解ける. アスベクト比最適化なども含めた整数計画によるアプローチも はかられている.
三角形分割を応用上も役立つものにしているのは, ドロネー三角形分割あるいはドロネー図である. これはボロノイ図の双対グラフとして定義される. ここでは, アルゴリズム的にも 有用な定義を与えておく. 2次元の点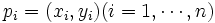 に対して, 新たに
に対して, 新たに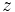 軸を考え, 3次元の点
軸を考え, 3次元の点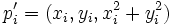 を対応させる. このとき,
を対応させる. このとき,  の3次元の凸包の
の3次元の凸包の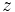 軸に関する下側境界 を
軸に関する下側境界 を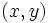 平面に正射影したものを,
平面に正射影したものを, 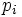
 のドロネー図 と定める.
のドロネー図 と定める.
ドロネー三角形分割は, 各三角形の外接円が他の点を内部に含まない三角形分割 として特徴づけられる. ドロネー三角形分割でないと, 点集合の中で凸四角形 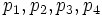 の三角形分割で, その三角形の外接円が他の点を含んでいる ものが存在する. このとき使っている対角線をもう1つの対角線に取り換えると, 局 所的に外接円に残りの1つの点は入らなくなる. 対角線を入れ換えることを対角変形といい, このように局所的にドロネー図に近付ける方向をドロネー対角変形と いう. 2次元では任意の三角形分割から
の三角形分割で, その三角形の外接円が他の点を含んでいる ものが存在する. このとき使っている対角線をもう1つの対角線に取り換えると, 局 所的に外接円に残りの1つの点は入らなくなる. 対角線を入れ換えることを対角変形といい, このように局所的にドロネー図に近付ける方向をドロネー対角変形と いう. 2次元では任意の三角形分割から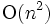 回ドロネー対角変形を行なう ことで, 必ずドロネー三角形分割に変換できる.
回ドロネー対角変形を行なう ことで, 必ずドロネー三角形分割に変換できる.
ドロネー三角形分割は, 上述のような様々な最適化基準を満たすが, その多く はこのドロネー対角変形によりその基準が改善されるという論法で証明され る. その場合, 最小角最大を例にすると, 全ての角度を小さい順に並べたベク トルについて, ドロネー三角形分割は辞書式順序で最大なベクトルを与えることも示すことができる.
三角形分割を2変数関数 の内挿関数
の内挿関数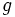 に適用した際, 曲面の三角形パッチによる近似の粗さの度合を
に適用した際, 曲面の三角形パッチによる近似の粗さの度合を
![\textstyle {\sum}_{S_i\in\tau}\int_{S_i}
\left[
\left(\partial g/\partial x\right)^2+
\left(\partial g/\partial y\right)^2
\right]{\rm d}x{\rm d}y
\,](https://cdn.weblio.jp/e7/img/dict/orjtn/a19ec67f5c68c914f17b2c2a759469ee.png) で定義すると, ドロネー対角変形は粗さ度を改善し, 最適性が導かれる. 最大最小包含円最小性は, 放物線のポテンシャル関数の性質によっている.
で定義すると, ドロネー対角変形は粗さ度を改善し, 最適性が導かれる. 最大最小包含円最小性は, 放物線のポテンシャル関数の性質によっている.
高次元の三角形分割の構造は一般に難しい. 三角形(単体)の個数も一定ではなく, 一般化された高次元対角変形により任意の三角形分割間で変換できるかどうかもわかっ ていない. 3次元で, 非凸の多面体の内部を新しい点を導入することなく四面体に分割することができるかどうかという問題は, NP困難である.
高次元三角形分割の性質のよい有用な部分クラスとして, 正則三角形分割(regular triangulation)がある. これは, 点集合 に対して新たなもう1次元方向を考え, その方向に各点に高さを与え, その分だけ新しい次元方向に持ち上げた点集合の凸包の下側境界を元の空間に正射影することにより得られるものである. もし, その凸包の下側境界にすべてのもち上げられた点がのっており, さらにそれらが一般の位置にあれば, 正射影されたものはまさしくこれまでの定義の三角形分割である. 正則三角形分割では与えられた点で三角形分割の頂点として使われないものもある. 2次元でも正則でない三角形分割は存在する.
に対して新たなもう1次元方向を考え, その方向に各点に高さを与え, その分だけ新しい次元方向に持ち上げた点集合の凸包の下側境界を元の空間に正射影することにより得られるものである. もし, その凸包の下側境界にすべてのもち上げられた点がのっており, さらにそれらが一般の位置にあれば, 正射影されたものはまさしくこれまでの定義の三角形分割である. 正則三角形分割では与えられた点で三角形分割の頂点として使われないものもある. 2次元でも正則でない三角形分割は存在する.
ドロネー三角形分割は正則であり, 正則三角形分割は高次元の場合も任意の2つの正則三角形分割は一般化対角変形で変換することができ, 2次元の三角形分割に通じるよい性質をもっている. さらに, 正則三角形分割は凸多面体と密接な関係をもった概念で, 数学・組合せ論で色々な展開が図られている. 詳細は [1] 参照.
[1] 今井桂子, 「三角形分割全体の離散構造」, 『離散構造とアルゴリズムVI』 (藤重悟編), 近代科学社, 1999.
三角測量
(triangulation から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/05/02 03:16 UTC 版)
| 測地学 | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
 |
||||||||||||||||||||||||
| 基本 | ||||||||||||||||||||||||
| 概念 | ||||||||||||||||||||||||
| 技術 | ||||||||||||||||||||||||
| 基準(歴史) | ||||||||||||||||||||||||
|
||||||||||||||||||||||||

三角測量(さんかくそくりょう)は、ある基線の両端にある既知の点から測定したい点への角度をそれぞれ測定することによって、その点の位置を決定する三角法および幾何学を用いた測量方法である。その点までの距離を直接測る三辺測量と対比される。既知の1辺と2か所の角度から、三角形の3番目の頂点として測定点を決定することができる。
三角測量はまた、三角網(さんかくもう)と呼ばれる非常に巨大な三角形群の正確な測量を行うことも指すことがある。これはヴィレブロルト・スネル(スネリウス)が1615年から1617年にかけて行った業績に由来している。スネルは、三つの既知の点に対する未知の点の角度を、既知の点からではなく未知の点から測定して、その点の位置を確定する方法(後方交会法)を示した。より規模の大きな三角形を最初に測定することにより、測量誤差を最小化できる。そうすれば、その三角形の内部の点は三角形に対して正確に位置を測定することができる。こうした三角測量法は、1980年代に衛星測位システムが登場するまで、大規模精密測量に用いられてきた。
用途
測定対象の空間次元と配置を決定するために、光学3次元測量システムは三角測量の方法を利用する。基本的にこうしたシステムは対象物を測定する二つのセンサーで構成されている。二つのうち一つは典型的にはデジタル式のカメラで、もう一方はカメラまたは映写機となっている。各センサーの中心および対象物表面上の点が空間上に三角形を構成する。この三角形において、センサー間の距離が基線bで既知でなければならない。この基線とセンサーに投影される光の角度を決定することで、投影光の交点の3次元座標を三角関数から計算することができる。
原理
ある点と二つの基準点が為す三角形の辺と角度が測定されていれば、その点の座標および距離はその三角形の辺の長さを計算することで求めることができる。
以下の数式は平坦なユークリッド平面において適用されるものである。これは距離が地球の曲面に比べて有意な長さになってくると不正確になるが、球面三角法を使えばより複雑な計算方法で求めることができる。

右の図に示すように、角度を計測した地点間の距離を


今日では三角測量は、測量、航海、計量学、位置天文学、両眼視、モデルロケット、兵器の照準といった多目的に使用されている。
三角形を利用して距離を測定するのは古代に遡る。紀元前6世紀の古代ギリシアの哲学者タレスは、ピラミッドの影の長さを測り、また同時刻における自分自身の影の長さを測って、自分の身長との比から相似な三角形を使ってピラミッドの高さを測定していた[1]。また崖の上から沖に見える船までの距離を、横方向にある既知の滝までの見通し水平距離を測り、これを崖全体の高さまで拡大することにより測定していた[2]。こうした方法は古代エジプト人にも知られていた。これより1000年ほど古いリンド数学パピルスに出てくる問題57番では、傾きを距離と高さの比で定義しており、今日の勾配の逆数に当たる。傾きと角度は、後のアラブのアリダードの前身である、ギリシア人がディオプトラと呼ぶ測定棒で測った。この器具を使って離れたところから距離を測定する方法についてのこの時代の詳細な説明は、アレクサンドリアのヘロンによる「ディオプトラ」にあり、これはアラブでは翻訳されて残ったが、ヨーロッパにおいては失われてしまった。中国では、裴秀が正確な地図作りの6原則の5番目として「直角と鋭角を測る」を挙げており、これは正確に距離を測るために必要なことであった[3]。また劉徽は、到達することのできない場所までの高さを求める方法として、上述したような計算方法を示していた[4][5]。
ローマ時代の土地測量の専門家、agromensoresと呼ばれる人々には、三角測量が使われていなかったことは明らかである。しかしアラブのイブン・アル=サッファーなどによるアストロラーベに関する文献を通じて中世のスペインに導入された[6]。アブー・ライハーン・アル・ビールーニーもまた三角測量を利用して地球の大きさを測定したり、さまざまな場所の間の距離を測ったりした[7]。簡素化されたローマの技術は、プロの測量技術者の使うより洗練された技術と共存していたものと思われる。しかしこうした技術がラテン語に翻訳されることは滅多になく、11世紀の測量に関するマニュアルGeomatria incerti auctorisが数少ない例外であった。こうした技術は、ヨーロッパのほかの地域は非常にゆっくりと浸透していったように見える[6]。スペインにおいてこうした技術の認知が広がり使われていたことは、1300年頃から角度を測定するために専用に使われていた中世のヤコブの杖という道具や、現存する最古のものとしては1296年の物がある、精密に海岸を測量した羅針儀海図によって証明されるだろう。
ゲンマ・フリシウスと地図を作るための三角測量
測量による地図作成の方法の古典的なものに導線法(旗や綱などを用いて距離と角度を繰り返し測量していく方法)があるが、この方法では途中の障害物などで誤差を生じやすく大規模な地図を作成するには大がかりな作業を伴う[8]。
オランダの地図製作者ゲンマ・フリシウスは、1524年のペトルス・アピアヌスによるCosmographicaの新版への付録という形で、1533年にLibellus de Locorum describendorum ratione(土地を表現する方法に関する冊子)を出し、その中で地図を作るために遠く離れた場所を正確に測定する方法として三角測量を使うことを提案した。これはとても影響が大きく、技術はドイツ・オーストリア・オランダなどに広がった。天文学者のティコ・ブラーエはスカンジナビアにおいてこの方法を適用し、彼の天文台があるヴェン島の詳細な三角測量を、エーレスンド海峡の両側にある目標物を基準として1579年に完成させ、1584年に島の土地計画を作った[9]。イングランドにおいてはこの世紀の中ごろ以降、ウィリアム・カニンガムのCosmographical Glasse(1559年)、ヴァレンティン・リーのTreatise of Measuring All Kinds of Lands(1562年)、ウィリアム・ボーンのRules of Navigation(1571年)、トーマス・ディッグスのGeometrical Practise named Pantometria(1571年)、ジョン・ノーデンのSurveyor's Dialogue(1607年)など、多くの本でフリシウスの方法が見られるようになった。クリストファー・サクストンも1570年代の彼の地図において特徴となるものを配置するために、粗雑ではあるが三角測量を使った可能性があると示唆されているが、一方で見晴らしの良い点からおおまかな方向感覚をつかんで、そこまでの距離を単に当て推量で決めただけであると反論されてもいる[10]。
ヴィレブロルト・スネルと現代の三角網
現代のシステマティックな三角網の使用は、オランダの数学者ヴィレブロルト・スネル(スネリウス)が1615年にアルクマールからベルヘン・オプ・ゾームまでおよそ110 kmを33の三角形を含む四角形の連鎖を利用して測定したことに始まる。この二つの町はほぼ同一子午線上にあって、緯度にして1度離れており、この測定から地球の円周長を求めることができた。この業績は1617年の本Eratosthenes Batavus(オランダのエラトステネス)に示されている。スネルは、平面における公式をどのように地球の丸みに対応させて修正するかの方法を計算した。彼はまた、三角形の内側にある点の位置を、その地点において三角形の辺がなす角度から計算する後方交会法を示した。これは、コンパスを使わなければならない頂点の方位を求める方法よりも正確に測定することができる。これにより、まず1次の大規模三角網を最初に測量し、その後2次的な地点を1次網の中で決定していくという考えが生まれた。ただし、スネルの使用した測量器は極めて単純なもので腕木の両端に糸を張って見通しをつけただけのものであったため結果はあまり正確ではなかった[11]。
スネルの測定した子午線は正確ではなかったが、彼の創案した測量の方法が優れた方法であることがわかると各国で三角測量が行われるようになった[12]。スネルの方法は、1669年から1670年にかけてパリ子午線上で緯度1度の長さをパリから北へアミアン近郊のスルドンの時計塔まで13の三角形の連鎖により測量したジャン・ピカールに引き継がれた。器具の改良と精度の向上により、ピカールは地球の半径をかなり正確に測定した最初の人物となった。18世紀を通じて有名なカッシーニ家の人間によりこの仕事はさらに進められた。1683年から1718年までの間、ジョヴァンニ・カッシーニとその息子ジャック・カッシーニはパリ子午線をダンケルクからペルピニャンまで測量した。1733年から1740年まで、ジャックとその息子セザール・カッシーニは子午線弧の再測量を含む全国土の最初の三角測量を行い、1745年に正確な原理に基づく初めてのフランスの地図を出版した。
この時点までに三角測量の技術は、地域的な地図作りに対しては十分確立された。しかし他の国が全国土に渡る地図を作るための詳細な三角網の測量を始めるのは18世紀も末になってからであった。
イギリス陸地測量部(オードナンス・サーベイ)は1783年にグレートブリテン島の基本となる三角測量を開始したが、完了したのは1853年のことになった。1801年に開始されたインド大三角測量では、エベレストやその他のヒマラヤ山脈の山々を三角測量し地図を作った。ナポレオン帝政下のフランスでは、ジャン・トランショによって1801年にフランスの三角網がドイツのラインラントまで拡大され、1815年以降になってプロイセン王国の将軍カール・フォン・ミュフリンクによって完成された。
この時期、有名な数学者カール・フリードリヒ・ガウスによって三角測量には優れた改良が加えられ他の方法を凌駕することとなった[13]。1821年から1825年にかけてガウスはハノーファー王国の三角測量を委託された。当時、三角測量には教会の塔など高い建物が利用され、ガウスも教会の塔を目標に考えていた[14]。しかし、1820年、ガウスが教会の塔を目印に三角測量を行おうとしたところ、空が霞んでいたため塔の姿を確認できなかったが、塔の位置は塔の色ガラスの反射で確認することができた[14]。そこで日光の反射によって位置を示すヘリオトロープ(回照器)が三角測量に用いられるようになった[14]。ガウスはヘリオトロープや櫓による測量方法の改良のほか、観測結果の整理法として未知数より実測値が多い時に大規模な連立方程式問題のもっとも一致する解を決定する最小二乗法を考案した[15]。
今日、測量のための大規模な三角網は1980年代以来確立した衛星測位システムにおおむね置き換えられている。しかし初期の測量の基準点はなお、1936年から1962年にかけてのグレートブリテン島再三角測量のために造られたコンクリート製三角点や、1816年から1855年にかけてのシュトルーヴェの測地弧の三角測量のために造られた、現在はユネスコの世界遺産に登録されている三角点のように、価値のある歴史遺産として残されている。
天文学において地球から星までの距離計測に用いられているが[16]、距離が離れると年周視差が小さくなることから1万光年程度が限界となるため[17]、他の計測法を併用する[18]。
宇宙探査機は通信用アンテナを地球に向け続けるために2つの恒星を使った三角測量で位置を計算しているが、地球に近く非常に明るい恒星として太陽とカノープスが使われている。
日本における実用化
北海道開拓使の開拓次官黒田清隆の招聘により来日したホーレス・ケプロンは、北海道の開拓にあたり、北海道の地理・気候を調査し、三角測量を行う必要性を指摘した[19]。これに基づき開拓使測量長に任命されたジェームズ・R・ワッソンらお雇い外国人を中心として1873年から勇払地方を基点に測量が進められ、1875年12月に「北海道実測図」が刊行された[20]。明治5年の工部省の測量士による、イギリス人マックスウェン(もしくはマクヴェイン)を中心とした東京での測量の先行例はあるものの[21]、これは日本における本格的な三角測量による地図作成の先駆けとなるものである[22][注 1]。
脚注
- ^ Diogenes Laërtius, “Life of Thales”, The Lives and Opinions of Eminent Philosophers 2008年2月22日閲覧。 I, 27
- ^ Proclus, In Euclidem
- ^ Joseph Needham (1986). Science and Civilization in China: Volume 3, Mathematics and the Sciences of the Heavens and the Earth. Taipei: Caves Books Ltd. pp. 539-540
- ^ 劉徽, 『海島算経』
- ^ Kurt Vogel (1983; 1997), A Surveying Problem Travels from China to Paris, in Yvonne Dold-Samplonius (ed.), From China to Paris, Proceedings of a conference held July, 1997, Mathematisches Forschungsinstitut, Oberwolfach, Germany. ISBN 3-515-08223-9.
- ^ a b Donald Routledge Hill (1984), A History of Engineering in Classical and Medieval Times, London: Croom Helm & La Salle, Illinois: Open Court. ISBN 0-87548-422-0. pp. 119-122
- ^ O'Connor, John J.; Robertson, Edmund F., “Abu Arrayhan Muhammad ibn Ahmad al-Biruni”, MacTutor History of Mathematics archive, University of St Andrews.
- ^ 『地図の話』123-128頁。
- ^ Michael Jones (2004), "Tycho Brahe, Cartography and Landscape in 16th Century Scandinavia", in Hannes Palang (ed), European Rural Landscapes: Persistence and Change in a Globalising Environment, p.210
- ^ Martin and Jean Norgate (2003), Saxton's Hampshire: Surveying, University of Portsmouth
- ^ 『地図の話』130頁。
- ^ 『地図の話』131頁。
- ^ 『地図の話』134頁。
- ^ a b c 『地図の話』133頁。
- ^ 『地図の話』136頁。
- ^ 質問6-1)星までの距離はどうやって測定するの? - 国立天文台
- ^ 『三角測量原理』による"星までの距離"の測定と限界について。 - オリックス・レンテック
- ^ 宇宙の質問箱-恒星編 - 国立科学博物館
- ^ “史跡「開拓使札幌本庁本庁舎跡および旧北海道庁本庁舎」保存活用計画(素案)”. 北海道. 2020年12月4日閲覧。
- ^ “北海道実測図”. 函館市中央図書館デジタル資料館. 2020年12月4日閲覧。
- ^ 加藤芳夫「明治初期の勇払基線と苫小牧の発展:わが国最初の系統的な基線測量と三角測量をめぐって」『地図』第16巻第4号、日本地図学会、1978年、11-16頁、doi:10.11212/jjca1963.16.4_11、ISSN 0009-4897、 NAID 130003812982。
- ^ “開拓使三角測量一本木基点”. 文化遺産オンライン. 2020年12月4日閲覧。
- ^ “江戸の数学 第一部 和算の歴史 第4章 実学としての和算 コラム 測量の方法”. 国立国会図書館. 2020年12月6日閲覧。
- ^ “伊能忠敬が仰いだ山々”. 2020年12月6日閲覧。
参考文献
- 武藤勝彦『地図の話』岩波書店、1949年。
関連項目
外部リンク
- triangulationのページへのリンク