さんかくけいぶんかつとは

Weblio 辞書 > 学問 > OR事典 > さんかくけいぶんかつの意味・解説

OR事典

三角形分割

読み方：さんかくけいぶんかつ
【英】：triangulation

概要

点集合の三角形分割とは, 2次元においてはその凸包を2-単体すなわち三角形に, 3次元では3--単体すなわち四面体に分割することである(四面体分割ともいう). 一般の次元の場合は単体分割あるいは簡単に三角形分割といわれる. 三角形分割は, 凸包・凸多面体とならんで基本的な幾何構造であり, 理論的に重要であるだけでなく, コンピュータグラフィクスや有限要素解析・内挿でのメッシュ生成など広く応用がある.

詳説

点集合の三角形分割(triangulation)とは, 2次元においてはその凸包を2-単体すなわち三角形に, 3次元では3-単体すなわち四面体に分割した構造である(四面体分割ともいう). 一般の次元の場合は単体分割あるいは簡単に三角形分割といわれる. 三角形分割は, 凸包・凸多面体とならんで基本的な幾何構造であり, 理論的に重要であるだけでなく, コンピューターグラフィクスや有限要素解析・内挿でのメッシュ生成など広く応用がある.

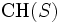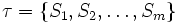$S=\{p_1,p_2,\ldots,p_n\}\,$ を $d\,$ 次元の $n\,$ 点の集合, $\mbox{CH}(S)\,$ を $S\,$ の凸包とする. $S\,$ の三角形分割 $\tau= \{S_1,S_2, \dots ,S_m\}\,$ とは, 次の条件を満たすものである.

$\begin{array}{ll} 1. & {\rm dim}\ {\rm CH}(S_i) = d, \ |S_i| = d+1, \ S_i\subseteq S \quad (i = 1,2,\dots,m) \\ 2. & \bigcup_{i=1}^m {\rm CH}(S_i) = {\rm CH}(S) \\ 3. & {\rm CH}(S_i)\cap{\rm CH}(S_j)={\rm CH}(S_i\cap S_j) \ (i \neq j) \end{array}\,$

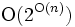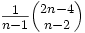平面上の一般の位置にある点集合 $S\,$ と $S\,$ の点をすべて用いる三角形分割を考える. $S\,$ のどの三角形分割も, オイラー(L. Euler)の公式から同じ数の三角形をもつ. また, 三角形分割の個数については, 三角形分割の平面性に着目して解析することにより ${\rm O}(2^{{\rm O}(n)})\,$ であることがいえる. 凸 $n\,$ 角形の頂点の場合は, 三角形分割の個数は $\textstyle \frac{1}{n-1}{2n-4\choose n-2}\,$ である. 動的計画法を用いることにより, 多角形内部の三角形分割の数を数えることは多項式時間で行えるが, 一般の点集合の三角形分割の個数を多項式時間で数えることができるかどうかは未解決の問題である. 多数の三角形分割の中から1つ選ぶ際の基準として代表的なものを上げる.

1. (最小角最大) 三角形分割での全角度の最小のもの(最小角)を最大にする

2. (最大角最小) 三角形分割での全角度の最大のもの(最大角)を最小にする

3. (重み最小) 三角形分割の辺長の総和を最小にする

4. (最大最小包含円最小) 三角形分割の各三角形の最小包含円(鈍角三角形の場合, 鈍角の対辺を直径にする円)のうち最大のものを最小にする

5. (最大アスペクト比最小) 三角形分割の各三角形のアスペクト比(三角形の外接円半径と内接円半径の比)の最大のものを最小にする

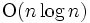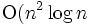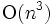他にも色々な評価規準が考えられる. 以下で述べるドロネー三角形分割は, このうち最小角最大, 最大包含円最小という性質を満たし(最大外接円最小も), かつ ${\rm O}(n\log n)\,$ の高速の時間で求めることができる. 最大角を最小にする ${\rm O}(n^2\log n\,$ )時間の動的計画法を用いたアルゴリズムも知られている. 一方, 辺長和を最小にする重み最小三角形分割問題の複雑さについてはまだよくわかっていないが, 2次元の場合は解法が与えられている. 点集合が凸 $n\,$ 角形の頂点集合の場合, 辺長和最小問題は動的計画法によって ${\rm O}(n^3)\,$ 時間で解ける. アスベクト比最適化なども含めた整数計画によるアプローチもはかられている.

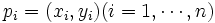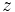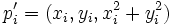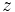三角形分割を応用上も役立つものにしているのは, ドロネー三角形分割あるいはドロネー図である. これはボロノイ図の双対グラフとして定義される. ここでは, アルゴリズム的にも有用な定義を与えておく. 2次元の点 $p_i=(x_i,y_i) (i=1,\cdots,n)\,$ に対して, 新たに $z\,$ 軸を考え, 3次元の点 $p'_i=(x_i,y_i,x_i^2+y_i^2)\,$ を対応させる. このとき, $p'_i (i=1,\cdots,n)\,$ の3次元の凸包の $z\,$ 軸に関する下側境界を 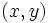$(x,y)\,$ 平面に正射影したものを,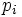 $p_i\,$ $(i=1,\ldots,n)\,$ のドロネー図と定める.

ドロネー三角形分割は, 各三角形の外接円が他の点を内部に含まない三角形分割として特徴づけられる. ドロネー三角形分割でないと, 点集合の中で凸四角形 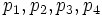$p_1,p_2,p_3,p_4\,$ の三角形分割で, その三角形の外接円が他の点を含んでいるものが存在する. このとき使っている対角線をもう1つの対角線に取り換えると, 局所的に外接円に残りの1つの点は入らなくなる. 対角線を入れ換えることを対角変形といい, このように局所的にドロネー図に近付ける方向をドロネー対角変形という. 2次元では任意の三角形分割から 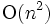${\rm O}(n^2)\,$ 回ドロネー対角変形を行なうことで, 必ずドロネー三角形分割に変換できる.

ドロネー三角形分割は, 上述のような様々な最適化基準を満たすが, その多くはこのドロネー対角変形によりその基準が改善されるという論法で証明される. その場合, 最小角最大を例にすると, 全ての角度を小さい順に並べたベクトルについて, ドロネー三角形分割は辞書式順序で最大なベクトルを与えることも示すことができる.

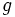三角形分割を2変数関数 $f\,$ の内挿関数 $g\,$ に適用した際, 曲面の三角形パッチによる近似の粗さの度合を $\textstyle {\sum}_{S_i\in\tau}\int_{S_i} \left[ \left(\partial g/\partial x\right)^2+ \left(\partial g/\partial y\right)^2 \right]{\rm d}x{\rm d}y \,$ で定義すると, ドロネー対角変形は粗さ度を改善し, 最適性が導かれる. 最大最小包含円最小性は, 放物線のポテンシャル関数の性質によっている.

高次元の三角形分割の構造は一般に難しい. 三角形(単体)の個数も一定ではなく, 一般化された高次元対角変形により任意の三角形分割間で変換できるかどうかもわかっていない. 3次元で, 非凸の多面体の内部を新しい点を導入することなく四面体に分割することができるかどうかという問題は, NP困難である.

高次元三角形分割の性質のよい有用な部分クラスとして, 正則三角形分割(regular triangulation)がある. これは, 点集合 $S\,$ に対して新たなもう1次元方向を考え, その方向に各点に高さを与え, その分だけ新しい次元方向に持ち上げた点集合の凸包の下側境界を元の空間に正射影することにより得られるものである. もし, その凸包の下側境界にすべてのもち上げられた点がのっており, さらにそれらが一般の位置にあれば, 正射影されたものはまさしくこれまでの定義の三角形分割である. 正則三角形分割では与えられた点で三角形分割の頂点として使われないものもある. 2次元でも正則でない三角形分割は存在する.

ドロネー三角形分割は正則であり, 正則三角形分割は高次元の場合も任意の2つの正則三角形分割は一般化対角変形で変換することができ, 2次元の三角形分割に通じるよい性質をもっている. さらに, 正則三角形分割は凸多面体と密接な関係をもった概念で, 数学・組合せ論で色々な展開が図られている. 詳細は [1] 参照.

参考文献

[1] 今井桂子, 「三角形分割全体の離散構造」, 『離散構造とアルゴリズム VI』 (藤重悟編), 近代科学社, 1999.

「OR事典」の他の用語

計算幾何：

レベルロバスト化技術一般距離ボロノイ図三角形分割位相優先法八分木凸包

索引トップ用語の索引ランキングカテゴリー

さんかくけいぶんかつに関連した本

FEMのための要素自動分割―デローニー三角分割法の利用 谷口健男 森北出版

>> 「さんかくけいぶんかつ」を解説文に含む用語の一覧

>> 「さんかくけいぶんかつ」を含む用語の索引

さんかくけいぶんかつのページへのリンク

さんかくけいぶんかつのページの著作権
Weblio 辞書情報提供元は参加元一覧にて確認できます。

1		井上和子
2		井上和子 (女優)
3		沓名環希
4		井上和子_(女優)
5		イノウエカズコ
6		行列のできる法律相談所
7		同居人カップルの殺人推理旅行
8		メガゾーン２３　PARTⅡ　秘密く・だ・さ・い
9		TPP
10		井上和子 (言語学者)

11		捗る
12		出不精
13		リーガル・ハイ
14		福利厚生
15		奇跡の人
16		アセスメント
17		自由民主党幹事長
18		石松千恵美
19		ダイバーシティ
20		友引

21		言葉
22		ハクビシン
23		未満
24		タカラダニ
25		先負
26		功罪
27		土曜ワイド劇場
28		ご指導ご鞭撻
29		セクシー・サイン　好き好き好き
30		注意喚起


	Copyright (C) 2012 （社）日本オペレーションズ・リサーチ学会 All rights reserved.

さんかくけいぶんかつとは？

OR事典

三角形分割

概要

詳説