メタ・ヒューリスティクス

OR事典

メタヒューリスティクス

読み方：めたひゅーりすてぃくす
【英】：metaheuristics

概要

組合せ最適化問題において, 遺伝アルゴリズム, アニーリング法, タブー探索といった発見的な探索を行う手法を総合した枠組. 暫定解に対し局所探索によって解の更新を行うが, 局所最適解に捕捉されることを防ぐための工夫を付加するというのが基本的な考え方である. 一般に最適性は保証できないが, 少ない計算時間で質の良い解を求めることができる場合が多いので極めて実用性が高く, 様々な問題への応用がなされている.

詳説

　メタヒューリスティクス (metaheuristics) とは組合せ最適化問題に対しての, 発見的解法の枠組みであり, 従来の数理的, 分析的手法に基づく厳密解法に対し, ある暫定解からより良い解を発見的に探索するための方法論である. 1) 個々の問題の性質に依拠しないより包括的な枠組みである, 2) 最適解を求めることではなく, より良い解を現実的な時間で求めることを目的とする, といった特徴が挙げられる. メタヒューリスティクスに含まれる多くの手法は局所探索法 (local search) を元にしているが, 局所最適解で探索が終了してしまうという欠点を補うためのさまざまな工夫がなされている[7].

　多スタート局所探索 (multi start local search) は適当な方法で生成した初期解からの局所探索法を繰り返し行うことにより, 改善された局所最適解を求めるものである.

　可変近傍法 (variable neighborhood search) は複数の近傍を定義し, 暫定解 （それまでに得られた最善解） に対しある近傍から一つ初期解を選択し, その解に対して局所探索法を適用するという手順を繰り返す. この反復において暫定解が更新されたか否かによって初期解を選択するための近傍を変える点に特徴がある.

　アニーリング法 (simulated aneealing) は局所探索法の実行過程に確率的な振る舞いを加え局所最適解に陥らないようにしたアルゴリズムであり, Kirkpatrickらによって提案された [2]. アニーリング法では改悪の方向への移行を確率で受け入れる. は温度と呼ばれる制御パラメータを含む関数で定義され, 目的関数が改悪される度合が大きくなれば小さくなるように定義される. 一般に用いられるのは, 変更にともなう目的関数値の変化量を(改悪ならば正、改良ならば負の値をとる)とすると,

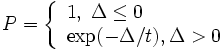
と定義される. パラメータは最初は大きな値に設定されるが、その後を徐々に小さくすることによって, 探索の初期の段階では広い領域を探索し, 後期では探索が最適解に落ち着くことをねらっている.

　タブー探索　(tabu search)　は局所探索法において局所最適解から脱出するため, 近傍内の最良解（改悪解であっても）へ移行するという操作を加えたものである [3, 4] . 一つの局所最適解とその近傍のみの移行という繰り返しを避けるために, 現在までの移行の履歴を保持し, 移行に制約を設ける. この制約をタブーという. またタブーにより良い局所最適解への移行を妨げる場合があるのでタブー保有期間と呼ばれる一定期間を経るとタブーは解消される. これにより局所最適解に陥ることなく広範囲の解を探索することが可能になる.

　遺伝アルゴリズム (genetic algorithm) は生物の形質遺伝による進化を組合せ最適化問題における解の進化, すなわち目的関数値を向上させることに利用した解法である [6]. まず候補解を記号列として表現したものを遺伝子と名付け, これらの遺伝子からなる集団に対し1) 次世代に子孫を残す解を選択し (選択), 2) 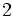つの親の遺伝子より子の遺伝子を生成し (交叉), 3) 遺伝子の一部を一定の確率で変化させ (突然変異), 4) 劣っている解は集団より除去する (淘汰), という操作を繰り返し行う. 交叉において遺伝子の特徴がどのように次の世代に遺伝していくかということはスキーマ定理 (scheme theorem) によって確率的に示されている [5]. 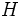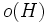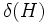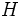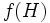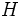ここでスキーマとは遺伝子を2進数で表現したときの部分列であり, その次元を, 定義長をとし, を次世代でスキーマを含む個体の数, スキーマを含む個体の適応度の平均値, 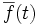を世代での個体の平均適応度とすると

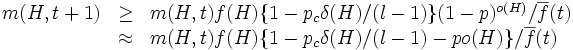
が成立する.

　遺伝アルゴリズムは進化的計算 (evolutionary computation), 進化的プログラミング (evolutionary programming) といった生物の遺伝, 進化の過程を模倣して最適化問題における最適解を探索するという枠組みの中のひとつであり、さらには人工生命 (artificial life) という生命システムをコンピュータでシミュレートする研究との関連においても注目されている.

---

参考文献

[1] G. Hansen and N. Mladenovic, "An Introduction to Variable Depth Search," in Meta-heuristics: Advances and Trends in Local Search Paradigms for Optimization, S. Voss, eds., Kluwer Academic Publishers, 1998.

[2] S. Kirkpatrick, C. D. Gellat and M. P. Vecchi, "Optimization by Simulated Annealing," Science, 220 (1983), 671-680.

[3] F. Glover, "Tabu Search I," ORSA Journal on Computing, 1 (1989), 190-206.

[4] F. Glover, "Tabu Search II," ORSA Journal on Computing, 2 (1989), 4-32.

[5] D. E. Goldberg, Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley, 1989.

[6] J. H. Holland, Adaptation in Natural and Artificial Sytems, University of Michigan Press, 1975.

[7] 柳浦睦憲, 茨木俊秀, 「組合せ最適化」, 朝倉書店, 2001.

「OR事典」の他の用語

組合せ最適化：	ファセット制約  フィボナッチヒープ  マッチング問題  メタヒューリスティクス  ラグランジュ緩和法  ロバース数  一般化割当問題
近似・知能・感覚的手法：	ベイジアンラフ集合  ホップフィールドネットワーク  ホーン節  メタヒューリスティクス  ラフセット  ラフメンバシップ値  ラフ集合

ウィキペディア

メタヒューリスティクス

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2022/10/28 05:43 UTC 版)

最適化問題 > 組合せ最適化 > メタヒューリスティクス

メタヒューリスティクスとは、組合せ最適化問題のアルゴリズムにおいて、特定の計算問題に依存しないヒューリスティクスのことである。 近年では、上記の定義から拡張され、特定の問題に依存しない、汎用性の高いヒューリスティクス全般を指すこともある。そのため、組合せ最適化問題のアルゴリズムに限らず、連続最適化問題に対するアルゴリズムも含む解釈も存在する。

概要

通常ある問題に対しての「解法」が存在するとき、その解法が適用できる範囲はその問題に対してのみである。

ところが近似アルゴリズムのように厳密な答えではなく、なるべく「答えに近い」まで拡大すると、局所探索法や貪欲法など複数の問題に対しても使用できる手法が存在する。

メタヒューリスティクスとは特定の問題に限定されず、どのような問題に対しても汎用的に対応できるように設計された、アルゴリズムの基本的な枠組みのことである。

言い換えればヒューリスティックアルゴリズムの内、特定の問題に依存せず手法のみが独立したものである。それゆえあらゆる問題に適用可能である。

このことはNP困難のような多項式時間で最適解を求めるアルゴリズムが存在しないと思われる問題などに対して有効である。

ただし、一般的にメタヒューリスティクスは特定の問題専用のヒューリスティクスより平均的な解の精度が劣ることが多い。これは汎用的な探索をするためには問題に対する事前知識を必要とせずに実装しなければならないので、それらを有効に使用することで解の探索を行う方法に対してどうしても不利な立場で探索を進める必要があるからである。

ノーフリーランチ定理

ノーフリーランチ定理によって平均的にはどの探索手法も同じ性能であることが示されて以来、「最も優れたメタヒューリスティクス」を求めることは無意味であることが示されている。この定理はしばしば「万能の探索アルゴリズムは存在しない」と表現されることがあり、メタヒューリスティクスに対するアンチテーゼとして用いられる。

しかしノーフリーランチ定理はあくまで「全ての問題に対する平均」であり問題空間をある程度まで限定した時の性能の善し悪しは論ずることはできない。また実際にメタヒューリスティックスを実装する場合は、探索効率を上げるためその問題の事前知識をさらに組み込んだりする例が多くある。それゆえ、この定理のみによってメタヒューリスティクスそのものに不要論を投げかけることはできない。

メタヒューリスティクスの例

進化的計算

• 進化的アルゴリズム
  • 遺伝的アルゴリズム(Genetic Algorithm)
  • 進化戦略(Evolution Strategy)
  • 進化的プログラミング(Evolutionary Programming)
  • 遺伝的プログラミング(Genetic Programming)

• 群知能
  • 蟻コロニー最適化(Ant Colony Optimization)
  • 粒子群最適化(Particle Swarm Optimization)
  • 人工蜂コロニーアルゴリズム(Artificial Bee Colony Algorithm)
  • ホタルアルゴリズム(Firefly Algorithm)
  • カッコウ探索(Cuckoo Search)
  • コウモリアルゴリズム(Bat Algorithm)
  • 狼探索アルゴリズム(Wolf Search Algorithm)
  • 花粉媒介アルゴリズム(Flower Pollination Algorithm)
  • バッタ探索アルゴリズム(Locust Search Algorithm)
  • トンボアルゴリズム(Dragonfly Algorithm)

• 差分進化(Differential Evolution)
• 風力駆動最適化(Wind Driven Optimization)
• ブレインストーミング最適化(Brain Storm Optimization)
• 渦最適化(Spiral Optimization)

近傍探索法

• タブー探索(Tabu Search)
• 焼きなまし法(Simulated Annealing)

その他のアルゴリズム

• シミュレーティド・エボリューション(Simulated Evolution)
• 人工免疫システム(Artificial Immune System)
• ニューラルネットワーク - 正確にはこのモデルを利用した各種アルゴリズム
  • バックプロパゲーション
  • ホップフィールド・ネットワーク
  • 自己組織化写像

ウィキペディア小見出し辞書

メタヒューリスティクス

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2021/04/15 03:07 UTC 版)

「探索」の記事における「メタヒューリスティクス」の解説

詳細は「メタヒューリスティクス」を参照 汎用的に使えるヒューリスティクスをメタヒューリスティクスという。 焼きなまし法 - 確率的探索アルゴリズムの一種 タブーサーチ - 探索が局所解で停滞するのを防ぐ技法 遺伝的アルゴリズム - 探索空間を縮小させるヒューリスティクスとして進化の考え方を使う。 蟻コロニー最適化 粒子群最適化