最急降下法
最急降下法
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2023/07/06 09:17 UTC 版)
最急降下法(さいきゅうこうかほう、英: gradient descent, steepest descent)[1]は、関数(ポテンシャル面)の傾き(一階微分)のみから、関数の最小値を探索する連続最適化問題の勾配法のアルゴリズムの一つ。勾配法としては最も単純であり、直接・間接にこのアルゴリズムを使用している場合は多い。最急降下法をオンライン学習に改良した物を確率的勾配降下法と呼ぶ。
尚、最急降下法の“最急”とは、最も急な方向に降下することを意味している。すなわち、収束の速さに関して言及しているわけではない(より速いアルゴリズムがあり得る)。
手法
n 次のベクトル x = (x1, x2, ... , xn) を引数とする関数を f (x) としてこの関数の極小値を求めることを考える。
勾配法では反復法を用いて x を解に近づけていく。k 回目の反復で解が x(k) の位置にあるとき、最急降下法では次のようにして値を更新する[1]。

| 一般 |
|
|---|---|
| 微分可能 |
|
| 凸縮小化 |
|
||||
|---|---|---|---|---|---|
| 線型 および 二次 |
|
| 系列範例 (Paradigms) |
|||||
|---|---|---|---|---|---|
| グラフ理論 |
|
最急降下法
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/11/16 07:46 UTC 版)
「回帰型ニューラルネットワーク」の記事における「最急降下法」の解説
詳細は「最急降下法」を参照 最急降下法は、関数の極小値を探し出すための一次の反復的最適化アルゴリズムである。ニューラルネットワークでは、非線形活性化関数が可微分であるという条件で、重みに関する誤差の微分係数に比例して個々の重みを変化させることによって誤差項を最小化するために使うことができる。これを行うための様々な手法はワーボス(英語版)、ウィリアムス(英語版)、ロビンソン(英語版)、シュミットフーバー(英語版)、ホッフライター(英語版)、パールマターらによって1980年代と1990年代初頭に開発された。 標準的手法は「通時的誤差逆伝播法(英語版)(Backpropagation through time、BPTT)」と呼ばれ、順伝播型ネットワークのための誤差逆伝播法の一般化である。誤差逆伝播法と同様に、BPTTはポントリャーギンの最小値原理(英語版)の後ろ向き連鎖(reverse accumulation)モードにおける自動微分の実例である。計算コストがより高いオンライン版は「実時間リカレント学習(Real-Time Recurrent Learning、RTRL)」と呼ばれる。これは、積み重ねられた接ベクトルを持つ前向き連鎖(forward accumulation)モードにおける自動微分の実例である。BPTTとは異なり、このアルゴリズムは時間について局所的だが、空間については局所的でない。 この文脈において、空間について局所的とは、単一ユニットの更新計算量が重みベクトルの次元において線形であるように、ユニットの重みベクトルが結合されたユニットとユニットそれ自身に蓄えられた情報のみを用いて更新できることを意味する。時間について局所的とは、更新が連続的に(オンラインで)起こり、BPTTのように任意の時間地平線内の複数の時間ステップではなく最も近い時間ステップにのみ依存することを意味する。生物学的ニューラルネットワークは時間と空間の両方に関して局所的であるように見える。 偏微分の再帰的計算について、RTRLはヤコビ行列を計算するために時間ステップ毎にO(隠れ層の数 × 重みの数) の時間計算量を持つのに対して、BPTTは任意の時間地平線内の全ての順方向活性化を記憶するという代償を払って、時間ステップ毎にO(重みの数) しか取らない。BPTTとRTRLの中間の計算量を持つオンラインハイブリッド版や、連続時間版が存在する。 標準的なRNN構造に対する最急降下法の大きな問題は、誤差勾配が重要な事象間の時間差の大きさに伴い指数関数的に急速に消失することである。BPTT/RTRL混成学習手法を組み合わされたLSTMはこれらの問題の克服を試みている。この問題は、ニューロンの文脈をそれ自身の過去状態に減らすことによって独立回帰型ニューラルネットワーク(IndRNN)でも解決され、次にニューロン横断的情報は続く層において探索できる。長期記憶を含む異なる範囲の記憶は勾配消失および爆発問題を起こさずに学習できる。 因果的再帰誤差逆伝播法(causal recursive backpropagation、CRBP)は、局所的に回帰したネットワークのためにBPTTおよびRTRL枠組みを実装し、組み合わせる。CRBPは最も一般的な局所回帰型ネットワークと連携する。CRBPアルゴリズムは大域誤差項を最小化できる。この事実はアルゴリズムの安定性を向上し、これは局所フィードバックを持つ回帰型ネットワークのための勾配計算技法に関する統一的な概観をもたらす。 任意の構造を持つRNNにおける勾配情報の計算のためのある手法は、シグナルフローグラフ図式導出(signal-flow graphs diagrammatic derivation)に基づく。この手法はBPTTバッチアルゴリズムを用い、ネットワーク感度計算に関するLeeの定理に基づく。これはWanおよびBeaufaysによって提案されたが、その高速なオンライン版はCampolucci、Uncini、およびPiazzaによって提案された。
※この「最急降下法」の解説は、「回帰型ニューラルネットワーク」の解説の一部です。
「最急降下法」を含む「回帰型ニューラルネットワーク」の記事については、「回帰型ニューラルネットワーク」の概要を参照ください。
- 最急降下法のページへのリンク
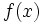 (ただし
(ただし 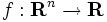 )を解くための
)を解くための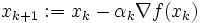 (
(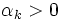 は
は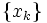 を
を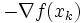 は,
は, 
