収束率
収束率
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/03/18 18:24 UTC 版)
この手法の利点は、計算に使用するプロセッサ数に比例して線形に性能が向上する点にある。つまり、問題のサイズに比例した計算量で、与えられた精度まで計算することができる。 密度が N i {\displaystyle N_{i}} の格子 i {\displaystyle i} 上で、微分方程式の近似解を(与えられた精度まで)求めることを考える。 K {\displaystyle K} を格子上での解の計算に関する定数、また隣り合う格子の密度の比 ρ = N j + 1 / N j < 1 {\displaystyle \rho =N_{j+1}/N_{j}<1} は常に一定であるとする。格子 i + 1 {\displaystyle i+1} の解を用いて、格子 i {\displaystyle i} 上での解が W i = ρ K N i {\displaystyle W_{i}=\rho KN_{i}} の計算量で求められるとすると、 W k = W k + 1 + ρ K N k {\displaystyle W_{k}=W_{k+1}+\rho KN_{k}\,} 特に最も細かい格子 N 1 {\displaystyle N_{1}} に関して W 1 = W 2 + ρ K N 1 {\displaystyle W_{1}=W_{2}+\rho KN_{1}\,} の関係が格子 k {\displaystyle k} 上での計算量に関して成り立つ。これらと N k = ρ k − 1 N 1 {\displaystyle N_{k}=\rho ^{k-1}N_{1}} の関係から、 W 1 = K N 1 ∑ p = 0 n ρ p {\displaystyle W_{1}=KN_{1}\sum _{p=0}^{n}\rho ^{p}} が得られる。幾何級数を使えば、(有限の n {\displaystyle n} について) W 1 < K N 1 1 1 − ρ {\displaystyle W_{1}<KN_{1}{\frac {1}{1-\rho }}} なので、解は O ( N ) {\displaystyle O(N)} の計算時間で得られることが分かる。
※この「収束率」の解説は、「マルチグリッド法」の解説の一部です。
「収束率」を含む「マルチグリッド法」の記事については、「マルチグリッド法」の概要を参照ください。
- 収束率のページへのリンク
 -収束率が
-収束率が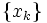 が
が 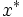 に
に 次
次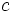 と
と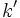 がとれて
がとれて 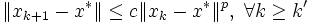 が
が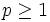 とし,
とし, 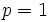 のときは
のときは 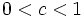 とする. 特に,
とする. 特に, 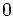 に
に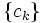 と
と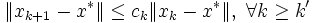 が
が