確率分布
確率分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2024/03/24 05:18 UTC 版)
 | この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。(2011年11月) |
確率分布(かくりつぶんぷ、英: probability distribution)は、確率変数に対して、各々の値をとる確率全体を表したものである。日本産業規格では、「確率変数がある値となる確率,又はある集合に属する確率を与える関数」と定義している[1]。
概要
例えば、「サイコロ2個を振ったときの出た目の和」は確率変数である。この確率変数 X に対する分布は次の表のようになる。
| X の取る値 n | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| P(X の値が n を取る) | 1/36 | 2/36 | 3/36 | 4/36 | 5/36 | 6/36 | 5/36 | 4/36 | 3/36 | 2/36 | 1/36 |
すなわち、離散型確率変数である場合は、確率分布とは確率変数の値にその確率(確率質量)を対応させる関数(確率質量関数)のことであると言うこともできる。しかし、例えば「次に電話がなるまでの時間」といった、連続型確率変数の場合は、確率変数値での確率が全て 0 となり、確率分布を確率質量関数で表すことができない。
「次に電話がなるまでの時間」は確率変数である。この確率変数 X の分布が次のようになったとする。
| X の値が取る範囲 I | 1時間以内 | 1–2時間後 | 2–3時間後 | 3–4時間後 | 4時間以上先 |
|---|---|---|---|---|---|
| P(X が I の範囲の値を取る) | 1/2 | 1/4 | 1/8 | 1/16 | 1/16 |
この場合の確率を全て表すには、全ての連続区間での確率を求めることになる。次の電話が a - b 時間後になる確率は次の式で表せる:
 一覧
一覧
 カテゴリ
カテゴリ
確率分布
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2020/11/06 09:03 UTC 版)
確率密度関数については、横軸をアフィン変換し平均を0、分散を1にすることを正規化という。正規化することで、標準正規分布関数との、あるいは確率密度関数同士の比較が容易になる。
※この「確率分布」の解説は、「正規化」の解説の一部です。
「確率分布」を含む「正規化」の記事については、「正規化」の概要を参照ください。
確率分布
「確率分布」の例文・使い方・用例・文例
- 正規分布という確率分布
確率分布と同じ種類の言葉
- 確率分布のページへのリンク
 を
を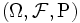 で
で
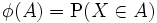 は
は 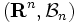
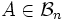 ,
, 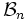 は
は 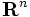
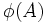 を
を 

