lasso

日本化学物質辞書Web

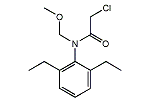
アラクロル

分子式：	C14H20ClNO2
その他の名称：	ラッソー、アラクロル、アラクロール、Lasso、Alachlor、CP-50144、2-Chloro-2',6'-diethyl-N-(methoxymethyl)acetanilide、2-Chloro-N-(2,6-diethylphenyl)-N-methoxymethylacetamide、アラネックス、アロクロル、ラゾ、メタクロル、Lazo、Alochlor、Alanex、ピラルゾ、Metachlor、Pillarzo、Methachlor、N-Chloroacetyl-N-methoxymethyl-2,6-diethylaniline、2-Chloro-N-(2,6-diethylphenyl)-N-(methoxymethyl)acetamide、N-(2,6-Diethylphenyl)-N-(methoxymethyl)chloroacetamide
体系名：	N-(2,6-ジエチルフェニル)-N-(メトキシメチル)-2-クロロアセトアミド、N-(メトキシメチル)-N-(2,6-ジエチルフェニル)-2-クロロアセトアミド、2-クロロ-N-(2,6-ジエチルフェニル)-N-メトキシメチルアセトアミド、2-クロロ-2',6'-ジエチル-N-(メトキシメチル)アセトアニリド、N-クロロアセチル-N-メトキシメチル-2,6-ジエチルアニリン、2-クロロ-N-(2,6-ジエチルフェニル)-N-(メトキシメチル)アセトアミド、N-(2,6-ジエチルフェニル)-N-(メトキシメチル)クロロアセトアミド

「日化辞Web」で詳細を見る

外国人名読み方字典

Lasso

名前 ラッソ； ラソ； ラッシュ； ラッソー

ウィキペディア

ラッソ回帰

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2023/09/26 22:35 UTC 版)

ラッソ回帰（ラッソかいき、least absolute shrinkage and selection operator、Lasso、LASSO）は、変数選択と正則化の両方を実行し、生成する統計モデルの予測精度と解釈可能性を向上させる回帰分析手法。1986年に地球物理学の文献で最初に導入され、その後1996年にロバート・ティブシラニ が独自に再発見して一般化した。

ラッソ回帰はもともと最小二乗法で定義されていた。最小二乗法の単純なケースでは、予測器の振る舞いについて多くの事実が分かる。すなわち、リッジ回帰やベストサブセット選択との関係、ラッソ係数予測といわゆるソフトしきい値処理（soft thresholding）との関係である。

一般化線形モデル、一般化推定方程式、比例ハザードモデル、M推定器など、さまざまな統計モデルに簡単に拡張できる。

動機

ラッソ回帰は、与えられた共変量の一部のみ最終モデルで使用することにより、回帰モデルの予測精度と解釈可能性を向上させるために導入された。

ラッソ回帰以前は、段階的選択が変数選択に広く用いられていた。これは、少数の共変量のみが結果と強い関係がある場合などには予測精度を向上させるが、それ以外の場合は、予測誤差を悪化させる可能性がある。 また、大きな回帰係数を縮小して過剰適合を減らすリッジ回帰も予測精度を向上させるために用いられていたが、リッジ回帰では共変量選択を実行しない。

ラッソ回帰は、回帰係数の絶対値の合計を固定値よりも小さくすることでこれらの目標を両方とも達成できる。これにより、特定の係数が強制的にゼロに設定され、これらの係数を含まないより単純なモデルが効果的に選択される。この考え方は、リッジ回帰に似ているが、リッジ回帰の場合はこれは係数のサイズを縮小するだけであり、ゼロに設定することはない。

基本形

ラッソ回帰はもともと最小二乗法の場面で導入された。このケースを最初に検討することは有益である。

それぞれが $p$

2次元のパラメータ空間（w₁, w₂）における、ラッソ回帰（L₁-norm）およびリッジ回帰（L₂-norm）の制約領域。

上で説明したように、ラッソ回帰は係数をゼロに設定できるが、表面的には類似しているように見えるリッジ回帰はできない。これは、2つのケースでの制約境界の形状の違いによるものである。ラッソ回帰とリッジ回帰の両方は、同じ目的関数を最小化すると解釈できる。

$\min _{\beta _{0},\beta }\left\{{\frac {1}{N}}\left\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}$

ラプラス分布は、平均で鋭くピークに達し、正規分布に比べて確率密度が集中している。

係数の事前分布として正規分布を仮定した場合の MAP推定値がリッジ回帰に相当するのと同様に、係数の事前分布としてラプラス分布を仮定した場合の MAP推定値がラッソ回帰に相当する。

ラプラス分布はゼロで鋭くピークに達し（その1次導関数は不連続）、確率分布は正規分布よりもゼロに近く集中する。 このことからも、なぜラッソ回帰では一部の係数をゼロに設定する傾向があるのに、リッジ回帰はそうではないのか、ということを説明できる。

$p(\mathbf {y} ,{\boldsymbol {\beta }}\mid \mathbf {X} )=p(\mathbf {y} \mid {\boldsymbol {\beta }},\mathbf {X} )\;p({\boldsymbol {\beta }}\mid \mathbf {X} )=\prod _{n=1}^{N}p(y_{n}\mid {\boldsymbol {\beta }},\mathbf {x} _{n})\;\prod _{k=0}^{K}p(\beta _{k})$

すなわち、

$\log {p(\mathbf {y} ,{\boldsymbol {\beta }}\mid \mathbf {X} )}=\sum _{n=1}^{N}\log {p(y_{n}\mid {\boldsymbol {\beta }},\mathbf {x} _{n})}+\sum _{k=0}^{K}\log {p(\beta _{k})}$

である。

ここで、 $\mathbf {y}$ の事前分布として平均 $\mathbf {X} {\boldsymbol {\beta }}$、分散 $\sigma ^{2}$ の正規分布を仮定すると、右辺第1項は

$\sum _{n=1}^{N}\log {\left({\frac {1}{{\sqrt {2\pi }}\,\sigma }}\exp {\left(-{\frac {(y_{n}-\mathbf {x} _{n}^{\top }{\boldsymbol {\beta }})^{2}}{2\sigma ^{2}}}\right)}\right)}=-N\log({\sqrt {2\pi }}\,\sigma )-{\frac {1}{2\sigma ^{2}}}\sum _{n=1}^{N}(y_{n}-\mathbf {x} _{n}^{\top }{\boldsymbol {\beta }})^{2}$

さらに、パラメータ ${\boldsymbol {\beta }}$ の事前分布として平均 $0$、分散 $2b^{2}$ のラプラス分布を仮定すると、右辺第2項は

$\sum _{k=0}^{K}\log {\left({\frac {1}{2b}}\exp {\left(-{\frac {|\beta _{k}|}{b}}\right)}\right)}=-(K+1)\log(2b)-{\frac {1}{b}}\sum _{k=0}^{K}|\beta _{k}|$

以上から、 $\lambda ={\frac {2\sigma ^{2}}{bN}}$ を用いて次のように表される。

$\log {p(\mathbf {y} ,{\boldsymbol {\beta }}\mid \mathbf {X} )}=-{\frac {N}{2\sigma ^{2}}}\left({\frac {1}{N}}\sum _{n=1}^{N}(y_{n}-\mathbf {x} _{n}^{\top }{\boldsymbol {\beta }})^{2}+\lambda \sum _{k=0}^{K}|\beta _{i}|\right)+\mathrm {const.}$

括弧内は、ラグランジュの未定乗数法に基づく記載と同等である。

一般化

エラスティックネット

2005年、Zou と Hastie は、ラッソ回帰に存在する欠点に対処するためにエラスティックネットを導入した。 ラッソ回帰は、標本数が共変量の数よりも少ないとき（ $n<p$）、標本数（ $n$ 個）までしか共変量を選択できない。 また、ラッソ回帰では高度に相関する共変量の組み合わせから1つしか共変量を選択しないことが多いため、共変量が強く相関しているならば、パフォーマンスがリッジ回帰に劣る場合がある。

エラスティックネットは $\ell ^{2}$ によるペナルティ項を追加することによってラッソ回帰を拡張し、下記の式を得る。

$\min _{\beta \in \mathbb {R} ^{p}}\left\{\left\|y-X\beta \right\|_{2}^{2}+\lambda _{1}\|\beta \|_{1}+\lambda _{2}\|\beta \|_{2}^{2}\right\},$

これは次の式を解くことと同じである。

${\begin{aligned}\min _{\beta _{0},\beta }\left\{\left\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}&{\text{ subject to }}(1-\alpha )\|\beta \|_{1}+\alpha \|\beta \|_{2}^{2}\leq t,\\&{\text{ where }}\alpha ={\frac {\lambda _{2}}{\lambda _{1}+\lambda _{2}}}.\end{aligned}}$

この問題は単純なラッソ回帰の形式で記述できる。

$\min _{\beta ^{*}\in \mathbb {R} ^{p}}\left\{\left\|y^{*}-X^{*}\beta ^{*}\right\|_{2}^{2}+\lambda ^{*}\|\beta ^{*}\|_{1}\right\}$

ただし、

$X_{(n+p)\times p}^{*}=(1+\lambda _{2})^{-1/2}{\binom {X}{\lambda _{2}^{1/2}I_{p\times p}}}$ 、   $y_{(n+p)}^{*}={\binom {y}{0^{p}}},\qquad \lambda ^{*}={\frac {\lambda _{1}}{\sqrt {1+\lambda _{2}}}}$ 、   $\beta ^{*}={\sqrt {1+\lambda _{2}}}\beta .$

そして、 ${\hat {\beta }}={\frac {{\hat {\beta }}^{*}}{\sqrt {1+\lambda _{2}}}}$ 、共変量が互いに直交する場合、

${\hat {\beta }}_{j}={\frac {{\hat {\beta }}_{j}^{\text{*,OLS}}}{\sqrt {1+\lambda _{2}}}}\max \left(0,1-{\frac {\lambda ^{*}}{\left|{\hat {\beta }}_{j}^{\text{*,OLS}}\right|}}\right)={\frac {{\hat {\beta }}_{j}^{\text{OLS}}}{1+\lambda _{2}}}\max \left(0,1-{\frac {\lambda _{1}}{\left|{\hat {\beta }}_{j}^{\text{OLS}}\right|}}\right)=(1+\lambda _{2})^{-1}{\hat {\beta }}_{j}^{\text{lasso}}.$

エラスティックネットのペナルティは、ラッソ回帰およびリッジ回帰のペナルティの組み合わせに相当する。

正規化パラメータ $\lambda _{1},\lambda _{2}$ は、交差検証法を用いたグリッド・サーチにより選択されることが多い。

Adaptive Lasso

2006年、オラクル性 oracle properties を持つように、罰則項に重みを乗じる手法が提唱された。

$\operatorname {arg\,min} _{\boldsymbol {\beta }}\left\|\mathbf {y} -\sum _{j=1}^{p}\mathbf {x} _{j}\beta _{j}\right\|+\lambda \sum _{j=1}^{p}w_{j}\left|\beta _{j}\right|.$

MI-LASSO

2013年、多重代入されたデータセットに対して、ラッソ回帰により変数選択する手法が提唱された。

正則化パラメータの選択

収縮の強度と変数の選択を制御する正則化パラメータ $\lambda$ を適切に選択することで、予測の精度と解釈可能性を向上することができる。正則化が強くなりすぎると、重要な変数がモデルから削除される、係数が過度に縮小される等の可能性がある。 正則化パラメータ $\lambda$ の選択には交差検証法がよく用いられる。

赤池情報量規準（AIC）やベイズ情報量規準（BIC）などの情報量規準は、交差検証法よりも計算が高速であり、小さいサンプルでもパフォーマンスが変動しにくいため、交差検証よりも好ましい場合がある。 情報量規準は、モデルのサンプル内精度を最大化することによって推定器の正則化パラメータを選択すると同時に、その有効なパラメーターの数/自由度にペナルティを課す。

関連項目

• モデルの選択
• ノンパラメトリック回帰
• ティホノフ正則化