トーラス

デジタル大辞泉

トーラス【Taurus】

読み方：とーらす

牡牛(おうし)座。

トーラス【torus】

読み方：とーらす

⇒円環面(えんかんめん)

スペース百科

トーラス

分類:ロケット
名称:トーラス/Taurus
打上げ国名・機関:アメリカ/アメリカ航空宇宙局(NASA)
開発機関・会社:オービタル・サイセンシズ社(OSC)
運用機関・会社:オービタル・サイセンシズ社(OSC)
打上げ場所:バンデンバーグ空軍基地
運用開始年:1994年解説:トーラスは、アメリカのベンチャー企業のオービタル・サイエンシズ社(OSC)が開発した小型衛星の商業打上げ機です。全部で4段式で、第1段には固体推進剤のキャスター120、第2段から上はOSCが開発したペガサス空中発射打上げ機の固体の第1/2/3段を流用しています。低コストをねらった簡略な構成で、1回の打上げ費用は1800万ドルになります。トーラスの1号機は、キャスター120に代えてピースキーパー大陸間弾道ミサイルの第1段を使用、1994年3月13日にアメリカ国防省先進研究計画局(DARPA)の衛星を打ち上げました。2号機は98年2月10日に、OSC自身の低高度通信衛星オーブコムの打上げに使われています。

トーラスをよく知るためのアラカルト
どんな形をして、どんな性能を持っているの?
打上げや飛行の順序はどうなっているの?
どんなものを打ち上げたの?
どのくらい成功しているの?
この他に、同じシリーズでどんな機種があるの?

分類:ロケットトーラスをよく知るためのアラカルト
どんな形をし、どんな性能を持っているの?
打上げや飛行の順序はどうなっているの?
どんなものを打ち上げたの?
どのくらい成功しているの?
この他に、同じシリーズでどんな機種があるの?1.どんな形をし、どんな性能を持っているの?
全固体推進剤ロケット4段式。全長22.6mm、直径2.4m、打ち上げ重量71.4t、初段推力131.2t。低高度軌道ペイロード1363キログラム、静止遷移軌道ペイロード431キログラム。

2.打上げや飛行の順序はどうなっているの?
トーラスは、ガントリー等の支えなしに、直接に発射台の上に立てられて、離昇します。第1段は83秒、第2段は72秒、第3段は73秒、第4段は240秒それぞれ燃焼し、ペイロードを衛星軌道に投入します。

3.どんなものを打ち上げたの?
DARPASAT、オーブコムがあります。4.どのくらい成功しているの?
2001年9月現在で6回打ち上げられ、5回成功しています。5.この他に、同じシリーズでどんな機種があるの?
OSCのペガサスと第2/3/4段が共通です。

核融合用語集

トーラス

読み方：とーらす

ドーナツ状の形をもつものをトーラスという。トカマクなどのプラズマはトーラスであり，軸のまわりに対称である。軸からプラズマの中心までの距離を大半径。軸に垂直で，上下の真ん中の面を赤道面という。トーラスの断面の横幅の半分を小半径という。断面の高さ方向の半分と小半径の比を楕円度という。大半径と小半径の比をアスペクト比という。これらの形状はプラズマの性能に大きな影響を与える。

ウィキペディア

トーラス

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/05/03 05:09 UTC 版)

この項目では、図形について説明しています。その他の用法については「トーラス (曖昧さ回避)」をご覧ください。

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方） 出典検索?: "トーラス" – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL（2015年5月）

トーラス

初等幾何学におけるトーラス（英: torus, 複数形: tori）、円環面、輪環面は、円周を回転して得られる回転面である。

いくつかの文脈では、二つの単位円周の直積集合 S¹ × S¹（に適当な構造を入れたもの）を「トーラス」と定義する。特に、位相幾何学における「トーラス」は、直積位相を備えた S¹ × S¹ に同相な図形の総称として用いられ、種数 1 の閉曲面（コンパクト二次元多様体）として特徴づけられる。このようなトーラスは三次元ユークリッド空間 R³ に位相的に埋め込めるが、各生成円をそれぞれ別の平面 R² に埋め込んで、それら埋め込みを保つような直積空間としての「トーラス」をユークリッド空間に埋め込むことは R³ では不可能で、R⁴ で考える必要がある。これはクリフォードトーラス（英語版） と呼ばれる、四次元空間内の曲面を成す。

アニュラスはトーラスではない

混同すべきでない関連の深い図形として、トーラスに囲まれた領域（三次元図形）すなわち「中身の詰まったトーラス」(solid torus) を、トーラス体、輪環体、円環体などと（対してもとのトーラスをトーラス面 (toroid) と）呼ぶこともある。また、中身の詰まったトーラスを単に「トーラス」(toroid) と呼ぶ場合があるので注意が必要である。また、同様に「円環」などと呼ばれる別の図形アニュラス（annulus、環帯）とも混同してはならない。

トーラス形

ドーナツの一種である、リングドーナツ

R = 大半径、r = 小半径

赤色の線がメリディアン、桃色の線がロンジチュード

詳細は「トーラス形」を参照

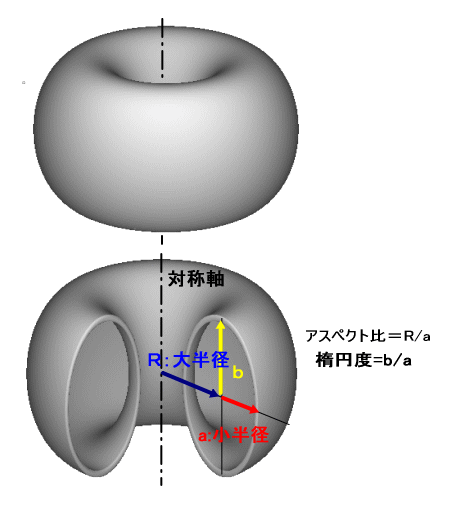
最もありふれたトーラスは、円（周）の外側に回転軸を置き得られる回転体、代表的なドーナツの形状の一つである「リングドーナツ」型で、いわゆる「ドーナツ型」である(ドーナツには球など様々な形があり、全てがトーラスの形状ではない。)。

トーラスの形と大きさを示すには大円の半径である大半径 R と、小円の半径である小半径 r (R > r) の2つの値が必要である（図）。小円とは回転体の断面の円、大円は小円の中心がなす円のことである。大円はトーラスの中心曲線（ちゅうしんきょくせん、core curve）ともいわれる。このトーラスは、xz 平面上の円 C

${\displaystyle C\colon (x-R)^{2}+z^{2}=r^{2}\quad (R>r>0)}$

正方形から円筒を、円筒からトーラスをつくる。

AとA、BとB（あるいはBとB、AとA）を繋げる。

繋げる順序が違うトーラス間の変形（アニメGIF）。4次元空間では穴あけ・伸縮なしでこの変形が可能である。

　

位相的トーラス

コーヒーカップとドーナツは同相である

位相幾何学的には、トーラスはどれだけ伸縮してもいい。有名な例は、ドーナツとコーヒーカップは同相である、というものである。つまり、コーヒーカップ（の表面）もトーラスである。

三葉結び目状のトーラス

また、結び目状になっているトーラスを考えることもできる。全ての結び目が円周に同相なように、結び目状になっているトーラスも標準的なトーラスと同相になる。ただし中心曲線の結び目が異なれば3次元空間上ではそれらは同位にならない。

性質

• トーラスの基本群は ⟨x, y : xyx⁻¹y⁻¹⟩ である。

多孔トーラス

トーラスは、2次元球面から2つの円板を除去し、その境界に円柱面 S¹×I の両端を貼り付けることによってつくることもできる。トーラスに対してさらにもう1つシリンダーをつけた曲面は二つ穴トーラス (double torus) と呼ぶことがある。これを繰り返してさらに多くの穴を持ったトーラスを考えることができ、穴の個数のことを種数という。また、シリンダーをつける操作は、新たなトーラスを連結和によって加えていることに相当する。

• 
  2つ穴トーラス
• 
  3つ穴トーラス

トーラス形多面体

詳細は「穿孔多面体」を参照

位相的にトーラス（あるいは多孔トーラス）である多面体はトーラス形多面体 (toroidal polyhedra) または穿孔多面体（穴のある多面体）と呼ばれる。

n次元トーラス

円周あるいは単純閉曲線 S¹ を 1 次元トーラスという。冒頭で述べた意味でのトーラスは S¹ × S¹ とあらわすことができる（片方の S¹ をメリディアン、もう片方の S¹ をロンジチュードと考えればよい）。一般に、n 次元トーラスあるいは簡単に n-トーラス Tⁿ とは S¹ の n 個の直積

${\displaystyle T^{n}=S^{1}\times S^{1}\times \cdots \times S^{1}}$

ウィキメディア・コモンズには、トーラスに関連するメディアがあります。