計算幾何学
【英】:computational geometry
概要
幾何学的な問題を解くための基本的なアルゴリズムの体系化をめざす学問分野. 1970年代から始まった若い分野であるが, アレンジメントやボロノイ図の計算をはじめ, すでに膨大なアルゴリズムが蓄積されている.
詳説
計算幾何学 (computational geometry) とは, 幾何的問題を効率よく解くための基本アルゴリズムの蓄積と体系化をめざす学問分野である. 計算幾何学という名称が初めて使われたのは Shamos の学位論文 [1] だと言われている. 1970年代の中頃に生まれたこの分野は, その後急速に発展し, 1980年代の中頃には相次いで標準的な教科書が出版された [2, 3, 4].
計算幾何学で扱う問題は多岐に渡るが, 以下に示すのはその中でも最も基本的なものである.
平面上に有限個の点が指定されたとき, どの点に最も近いかによって平面をそれぞれの点の勢力圏に分割した図形をボロノイ図 (Voronoi diagram) といい, 最初に与えた点を生成元という. ボロノイ図は自然界のパターンの解析, 地理的最適化など多くの応用に使われている.  個の生成元のボロノイ図は
個の生成元のボロノイ図は 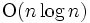 の計算量で作ることができ, これが最適であることもわかっている. ボロノイ図は, 空間の次元や距離を変えることによって多くの種類のものが定義できる. 上に述べたのはその中の最も基本的なもので, 点ボロノイ図 (Voronoi diagram for points) とよばれている.
の計算量で作ることができ, これが最適であることもわかっている. ボロノイ図は, 空間の次元や距離を変えることによって多くの種類のものが定義できる. 上に述べたのはその中の最も基本的なもので, 点ボロノイ図 (Voronoi diagram for points) とよばれている.
空間の点の集合  は, 「
は, 「 内の任意の 2 点を結ぶ線分が
内の任意の 2 点を結ぶ線分が  に含まれる」という性質を満たすとき凸集合とよばれる. 与えられた点の集合
に含まれる」という性質を満たすとき凸集合とよばれる. 与えられた点の集合  に対して,
に対して,  を含む最小の凸集合を
を含む最小の凸集合を  の凸包 (convex hull) という.
の凸包 (convex hull) という.  次元空間における
次元空間における  個の点の集合
個の点の集合  に対する凸包は,
に対する凸包は, 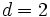 のとき
のとき 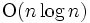 の計算量で,
の計算量で, 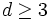 のとき
のとき 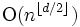 の計算量で求めることができる. ただし
の計算量で求めることができる. ただし 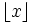 は
は  以下の最大の整数を表す. また, これより小さい計算量では求められないこともわかっている.
以下の最大の整数を表す. また, これより小さい計算量では求められないこともわかっている.
 を平面上に指定された
を平面上に指定された  個の点の集合とする.
個の点の集合とする.  の凸包の内部を,
の凸包の内部を,  に属すすべての点を頂点に使って三角形に分割した図形を,
に属すすべての点を頂点に使って三角形に分割した図形を,  を張る三角形分割 (triangulation) という.
を張る三角形分割 (triangulation) という.  を張る三角形分割は一般に何通りもある. その中で, 点ボロノイ図の双対図形として得られる三角形分割 (ドロネー図), 辺長の和が最小の三角形分割 (重み最小三角形分割) などが, 比較的ふっくらとした三角形を多く含む分割であるためによく調べられている. 前者は
を張る三角形分割は一般に何通りもある. その中で, 点ボロノイ図の双対図形として得られる三角形分割 (ドロネー図), 辺長の和が最小の三角形分割 (重み最小三角形分割) などが, 比較的ふっくらとした三角形を多く含む分割であるためによく調べられている. 前者は 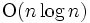 の計算量で構成できるが, 後者を構成する問題はNP困難か否かもわかっていない. 一方, 三角形の質は問わないで, どのような三角形を使ってもよいからともかく
の計算量で構成できるが, 後者を構成する問題はNP困難か否かもわかっていない. 一方, 三角形の質は問わないで, どのような三角形を使ってもよいからともかく  を張る三角形分割を作りたいという場合でも
を張る三角形分割を作りたいという場合でも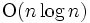 より小さい計算量では作れないことがわかっている. その意味でもドロネー図は重要な三角形分割である.
より小さい計算量では作れないことがわかっている. その意味でもドロネー図は重要な三角形分割である.
 次元空間に
次元空間に  個の超平面が与えられたとき, それらの超平面が互いに交差して空間を分割する構造はアレンジメント (arrangement) とよばれる.
個の超平面が与えられたとき, それらの超平面が互いに交差して空間を分割する構造はアレンジメント (arrangement) とよばれる. 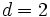 の場合は平面内の直線のアレンジメントであり, 平面を凸多角形に分割した構造である.
の場合は平面内の直線のアレンジメントであり, 平面を凸多角形に分割した構造である. 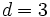 の場合は 3 次元空間内の平面のアレンジメントであり, 空間は凸多面体に分割される.
の場合は 3 次元空間内の平面のアレンジメントであり, 空間は凸多面体に分割される.
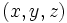 座標系をもつ3次元空間において,
座標系をもつ3次元空間において, 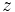 軸に平行ではない
軸に平行ではない 枚の平面が作るアレンジメントを
枚の平面が作るアレンジメントを 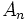 とする.
とする. 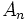 は空間をいくつかの凸多面体に分割するが, その境界となっているおのおのの凸多角形は,
は空間をいくつかの凸多面体に分割するが, その境界となっているおのおのの凸多角形は, 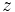 軸に平行な直線によって貫かれる順序によって,
軸に平行な直線によって貫かれる順序によって, 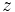 座標の大きい方から1層目, 2層目, 等と層に分類することができる. これらの階層は2次元ボロノイ図と密接な関係がある [4].
座標の大きい方から1層目, 2層目, 等と層に分類することができる. これらの階層は2次元ボロノイ図と密接な関係がある [4].
計算幾何学では, 各種幾何問題に対してそれを解く個別のアルゴリズムを追求するだけでなく, 異なる幾何構造の間の関係を調べ, それをアルゴリズムの開発に利用する努力もなされている. 異なる幾何構造をつなぐための代表的道具の一つは双対変換 (dual transformation) である. 最も素朴な双対変換は平面上の直線 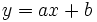 を点
を点 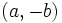 へ変換させるものである. この変換によって点は直線へ変換され, もとの平面での直線と点との接続関係は双対変換を施したあとも保たれる. このことを利用すると, たとえば平面上に指定された
へ変換させるものである. この変換によって点は直線へ変換され, もとの平面での直線と点との接続関係は双対変換を施したあとも保たれる. このことを利用すると, たとえば平面上に指定された 本の線分のすべてを通過する1本の直線を求める問題 (串刺し問題) は,
本の線分のすべてを通過する1本の直線を求める問題 (串刺し問題) は,  個のくさび形領域の共通部分を求める問題に帰着される. このように変換によって問題を扱いやすい別の問題へ帰着させる技術も計算幾何学では多数蓄積されている.
個のくさび形領域の共通部分を求める問題に帰着される. このように変換によって問題を扱いやすい別の問題へ帰着させる技術も計算幾何学では多数蓄積されている.
[1] M. I. Shamos, Computational Geometry, Ph.D. Thesis, Department of Computer Science, Yale University, New Haven, 1978.
[2] F. P. Preparata and M. I. Shamos, Computational Geometry -An Introduction, Springer-Verlag, New York, 1985.
[3] 伊理正夫監修, 腰塚武志編集, 『計算幾何学と地理情報処理』, 共立出版, 1986. (第2版, 1993).
[4] H. Edelsbrunner, Algorithms in Combinatorial Geometry, Springer-Verlag, Berlin, 1987.
計算幾何学
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/01/18 16:30 UTC 版)
計算幾何学(けいさんきかがく、英語: computational geometry)は、幾何学の言葉で述べることのできるアルゴリズムの研究をテーマとする計算機科学の一分野である。計算幾何学的アルゴリズムの研究から純幾何学的な問題が生じることもあり、またそのような問題は計算幾何学の一部であると考えられる。
概要
計算幾何学はコンピュータグラフィックスの発展、計算機支援のデザインや操作 (CAD/CAM) の研究分野としての側面を主な動機として展開されたが、計算幾何学における問題は、その多くが自然界における古典的な幾何学の問題である。
ほかに、計算幾何学の重要な応用は次のものがある。
計算幾何学の主な分科には次のようなものがあげられる:
- 組合せ論的計算幾何学[1]
- 離散的な存在としての幾何学的対象を扱う。この主題における下敷きとなる基礎的な教科書は、1975年に初めてこの意味で「計算幾何学」という用語を用いた、Preparata と Shamos[2]である。
- 数値計算幾何学[3]、計算機支援幾何学的デザイン[4]、幾何学的モデリング[5]
- 実世界の物体を CAD/CAM システムにおける計算機計算に適した形で表現することを第一に扱う。この分科は画法幾何学の更なる発展形と見ることができ、しばしばコンピュータグラフィックスや CAD に関する分野の一部と考えられる。この意味で用語「計算幾何学」が使われるようになったのは1971年[6]からのことである。
組合せ論的計算幾何学
組合せ論的計算幾何学における研究の第一の目的は、(点、線分、多角形、多面体などのような)基本的な幾何学対象の言葉で述べられる問題の解決に対して、効果的なアルゴリズムとデータ構造を開発することである。
これらの問題の中には、とても単純で計算機が出現するまではとても問題とは見なされていなかったようなものもある。例えば最近接点探索と呼ばれる、
平面上に与えられた n 個の点に対し、互いの距離がもっとも小さくなるような二点を求めよ。
という問題を考えよう。与えられた点の(n(n − 1)/2 個ある)全ての対に対してそれらの距離を計算すれば、最短の距離にある対を取り出すことができる。このブルート・フォースアルゴリズムはランダウの記号を使えば O(n2) 時間である(つまり、実行時間が点の数の自乗に比例する)。計算幾何学における古典的な結果として O(n log n) 時間だけ掛かるアルゴリズムが定式化された。確率的アルゴリズムでは O(n) であることが期待され、同様に決定性アルゴリズムでは O(n log log n) 時間を持つことが発見された。
計算幾何学では、アルゴリズムが一千万や一億といったようなたくさんの点を含む非常に巨大なデータ集合の上で用いられることを想定して、計算量を非常に重要視する。巨大なデータ集合に対し、 O(n2) と O(n log n) との違いは、計算が数日掛かるか数秒で終わるかというくらいのはっきりした違いを生むのである。
問題の分類
組合せ論的計算幾何学における中心的な問題に関して、いくつかの判定法に従った異なる方法による分類が可能である。一般的には以下のような分類が区別される。
静的問題
これに分類される問題は、いくつか入力が与えられた状態で、それに対応する出力を構築または計算することが要求される。この種の基本的な問題として
- 凸包: 与えられた点の集合に対して、それらを全て含む最小の凸多角形・凸集合を計算する問題。ギフト包装法など。
- 線分交叉問題: 与えられた線分の集合に対して、それらの交点を求める問題。
- ドロネー三角形分割
- ボロノイ図: 与えられた点の集合に対して、それらの中で最も近い点に代表される部分に属するように空間を分割する問題。
- 線型計画問題
- 最近接点探索: 与えられた点の集合に対して、その中で最も互いの距離が短いふたつを選び出す問題。
- ユークリッド的最短経路問題: (多面体の障害物がある)ユークリッド空間において、与えられた二点を最短経路で結ぶ問題。
- 多角形の三角形分割: 与えられた多角形を、その内部にある三角形に分割する問題。
などが挙げられる。この種の問題に対する組合せ論的な計算量は、与えられた問題事例が要求する時間と空間(計算機のメモリ)によって評価される。
幾何学的問合せ問題
一般には幾何学的探索問題として知られる幾何学的問合せ問題において、入力は探索空間と問合せ(クエリ)の二つの部分からなり、それらは問題事例に応じてさまざまなものがある。探索空間はふつう、複数の問合せに効果的に応答することができるように、前処理されている必要がある。
基本的な幾何学的問合せ問題としては、
- 範囲探索: 点の集合を前処理して、要求された領域の内側にある点の数を効果的に数えられるように整列する。
- 点配置: 空間のセル分割が与えられたとき要求された点がどのセルに配置されるかを効果的に解答できるようなデータ構造を導出する問題。
- 最近接近傍探索: 点の集合を前処理して、要求された点に最も近い点を効果的に見つけられるように並べ替える。
- レイ・トレーシング: 空間内の物体の集合が与えられたとき、要求された半直線が最初にどの物体と交わるかを解答する効果的なデータ構造を求める問題。
などが挙げられる。探索空間を固定するとき、この類の問題に対する計算量は通常
- 探索に必要なデータ構造を構築するの必要な時間と空間、
- 問合せに応答するまでの時間(と場合によっては余分の空間)
によって評価される。探索空間を変更することが許される場合については後述の#動的問題を参照。
動的問題
もうひとつ大きな分類として動的問題があり、それは(入力する幾何学的要素を加えたり除いたりするような)入力の逐次変更に追随して繰り返し解を求める効果的なアルゴリズムの発見を目的とする。この種の問題に対するアルゴリズムは普通、動的データ構造を伴う。計算幾何学的な問題はどれも動的問題に作り変えることができる。例えば範囲探索問題は与える点を増減させることを考えることによって動的範囲探索問題に変形される。動的凸包問題は、たとえば(入力点を増減させるような)点集合の動的な変化に対しての、凸包の変化の様子を追う問題である。
この種の問題の計算量は
- 探索に用いるデータ構造の構築に必要な時間と空間、
- 探索されたデータ構造の探索空間における逐次変更に伴う修正に掛かる時間と空間、
- 要求に解答するための時間(と余分な空間)
によって評価される。
変種
問題の中には、文脈によってどちらのカテゴリーにも属するものとして扱わなければならないようなものもある。例えば次の
- Point in polygon: 点が与えられた多角形の内側にあるか外側にあるかどうかを決定せよ。
という問題を考えよう。多くの応用では単発のものとして扱って、静的な問題に属することになるだろう。たとえばコンピュータグラフィックスに関する応用の多くでは、マウスカーソルで画面のどの領域がクリックされたか知るというようなことがよくある問題である。しかし、応用の中には問における多角形は不変だが、点は問合せを表すようなものもある。例えば、入力する多角形が国境を表し、点が航空機の位置を表していて、航空機が領空侵犯しているかどうかを判定せよという問題などである。最後に、コンピュータグラフィックスについて上で述べた例に関して、CAD ソフトは入力データの変化を、点が多面体の中にあるかの問合せのスピードアップに活用するために、動的データ構造として格納する。
問合せ問題の文脈には、効果的なデータ構造や精緻な計算量評価に活用することができる、問合せの列の存在を期待するほうが合理的というようなものもある。たとえば、個々の問合せのどれに一番時間が掛かるかを知るよりも、一続きの複数の問合せの全体にかかる合計時間が最悪のものを知ることのほうが重要であるというような場合があるかもしれない。「償却解析」("amortized analysis") も参照。
数値的計算幾何学
この分科は幾何学的モデリングや計算機支援幾何学デザイン (CAGD) としても知られる。
中核となる問題は曲線や曲面のモデリングと表現である。
ここでの基本的な道具はベジエ曲線やスプライン曲線・スプライン曲面のような曲線のパラメータ表示および曲面のパラメータ表示である。非パラメトリックな手法としてはレベル集合がある。
応用分野には、造船、航空、自動車製品などが含まれる。現代における計算機の遍在性と能力が意味するのは香水ビンやシャンプーのボトルでさえ、1960年代の造船技師では考えられないような手法を用いてデザインを行っているということなのである。
脚注
- ^ 英: Combinatorial computational geometry または algorithmic geometry
- ^ Franco P. Preparata、Michael Ian Shamos (1985). Computational Geometry - An Introduction. Springer-Verlag. 1st edition: ISBN 0-387-96131-3; 2nd printing, corrected and expanded, 1988: ISBN 3-540-96131-3
- ^ 英: Numerical computational geometry、machine geometry
- ^ 英: computer-aided geometric design、CAGD
- ^ 英: geometric modeling
- ^ A.R. Forrest, "Computational geometry", Proc. Royal Society London, 321, series 4, 187-195 (1971)
関連項目
参考文献
- 浅野哲夫 (1990):「計算幾何学」、朝倉書店.
- 今井浩、今井桂子 (1994):「計算幾何学」、共立出版.
- 伊理正夫 (1986):「計算幾何学と地理情報処理」、共立出版. ※bit 別冊、1993年に第2版単行本化
- 杉原厚吉 (1998):「FORTRAN 計算幾何プログラミング」、 岩波書店.
- 浅野哲夫 (2007):「計算幾何: 理論の基礎から実装まで」、 共立出版, ISBN 978-4-320-12176-8.
- 杉原厚吉 (2013):「計算幾何学」、朝倉書店.
関連文献
雑誌
組合せ論的計算幾何学
以下は、出版された大手の幾何学的アルゴリズムに関する研究誌の一覧である。見るからに計算幾何学をはっきりと専門とする雑誌を優先し、計算機科学一般を目的とした雑誌やコンピュータグラフィックスに関する雑誌の幾何学的な出版物の割合は減らしてあることに注意されたい。
- en:ACM Computing Surveys
- en:ACM Transactions on Graphics
- en:Acta Informatica
- en:Advances in Geometry
- en:Algorithmica
- en:Ars Combinatoria
- en:Computational Geometry: Theory and Applications
- en:Communications of the ACM
- en:Computer Graphics and Applications
- en:Computer Graphics World
- en:Discrete & Computational Geometry
- en:Geombinatorics
- en:Geometriae Dedicata
- en:IEEE Transactions on Graphics
- en:IEEE Transactions on Computers
- en:IEEE Transactions on Pattern Analysis and Machine Intelligence
- en:Information Processing Letters
- en:International Journal of Computational Geometry and Applications
- en:Journal of Combinatorial Theory, series B
- en:Journal of the ACM
- en:Journal of Algorithms
- en:Journal of Computer and System Sciences
- Management Science
- Pattern Recognition
- en:Pattern Recognition Letters
- en:SIAM Journal on Computing
- en:SIGACT News; featured the "Computational Geometry Column" by Joseph O'Rourke
- en:Theoretical Computer Science
- en:The Visual Computer
外部リンク
計算幾何学
計算・幾何学と同じ種類の言葉
固有名詞の分類
- 計算・幾何学のページへのリンク

