おう‐りょく【応力】
おうりょく 応力
応力
応力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/08/01 22:53 UTC 版)
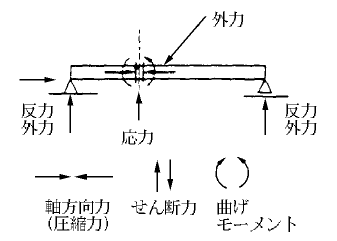
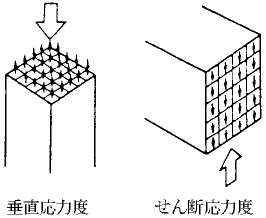
応力(おうりょく、ストレス、英: stress)とは、物体[注 1]の内部に生じる力の大きさや作用方向を表現するために用いられる物理量である。物体の変形や破壊などに対する負担の大きさを検討するのに用いられる。
注釈
出典
- ^ 平凡社大百科事典、応力の項、「応力の大きさは単位面積に作用する内力のおおきさにより定義され、これを応力度あるいは応力強さともいうが、一般には応力度のことを単に応力と呼び・・・」第2巻、p.831、平凡社、1984年11月2日 初版
- ^ 福井コンピュータ. “応力度”. 建築用語大辞典. ウェブリオ株式会社. 2013年8月12日閲覧。(ウェイバックマシンより)
- ^ 萩原芳彦 (2007年9月30日). “第5話 応力とは何”. 初学者のための材料力学四方山話. p. 3. 2011年12月25日閲覧。
- ^ 計量単位令 別表第一 項番23、応力、「一平方メートルにつき一ニュートンの応力」
- ^ 小林英男 & 轟章 2007, p. 29.
- ^ 渋谷陽二 2011, p. 66.
- ^ 「弾性力学」pp.8-9
- ^ 「弾性力学」pp.5-6
- ^ 「機械工学辞典」pp.567-568
- ^ 中村恒善 編 『建築構造力学 図説・演習Ⅰ』(2版)丸善、1994年、135頁。ISBN 4-621-03965-2。
- ^ a b c d e 「弾性力学」pp.10-15
- ^ 非線形CAE協会 編 『例題で学ぶ連続体力学』森北出版、2016年、66頁。ISBN 978-4-627-94821-1。
- ^ 野田直剛 et al. 1999, p. 18.
- ^ 渋谷陽二 2011, p. 34.
- ^ 渋谷陽二 2011, pp. 29–31.
- ^ 非線形CAE協会 編 『例題で学ぶ連続体力学』森北出版、2016年、70頁。ISBN 978-4-627-94821-1。
- ^ 非線形CAE協会 編 『例題で学ぶ連続体力学』森北出版、2016年、71頁。ISBN 978-4-627-94821-1。
- ^ a b c 「材料強度」pp.9-12
- ^ 大矢根守哉監修 『塑性加工学』(14版)養賢堂、1999年、76頁。ISBN 4-8425-0113-8。
応力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2019/12/09 05:58 UTC 版)
構造物のある部材に生じる力。軸方向力(軸力)N kN、せん断力Qxy kN、Qyz kN、曲げモーメントMxy kN⋅m、Myz kN⋅m、ねじりモーメント kN⋅mの計6個の値で表す(3次元の場合)。基本的にはすべての部材について、必要な値を計算する。
※この「応力」の解説は、「構造計算」の解説の一部です。
「応力」を含む「構造計算」の記事については、「構造計算」の概要を参照ください。
応力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2022/03/28 10:03 UTC 版)
詳細は「航空力学」を参照 翼桁に作用する応力としては、以下のようなものがある: 飛行中に機体を支持する主翼の揚力による上向の応力。これらの応力は、セスナ 310(英語版)などのように主翼端に燃料を搭載することによってある程度相殺することができる。 地上で静止している最中に、主翼自体の構造、翼内に搭載された燃料およびエンジンが主翼に搭載されている場合はその重量による下向き曲げ荷重。 対気速度および慣性による抗力荷重。 慣性モーメント荷重。 捻り下げ(英語版)による高速度での空気力学効果およびエルロン操作の結果としての操縦逆転(英語版)による翼弦(英語版)ひねり荷重。さらに、主翼から吊り下げられたエンジンの推力を変更することにってもひねり荷重が増減する。Dボックス構造は主翼のねじれを減少するのに有効である。 これらの荷重はエクストラ EA-300のような極端な曲技飛行を行う機体では、飛行中に急激に反転するので、このような飛行機の翼桁は大きな荷重倍数にも安全に耐えられるように設計されている。
※この「応力」の解説は、「翼桁」の解説の一部です。
「応力」を含む「翼桁」の記事については、「翼桁」の概要を参照ください。
応力
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2021/07/20 08:33 UTC 版)
結晶に応力を発生させると点欠陥が発生しやすくなる。さらに大きな応力を加えると点欠陥が集合して線欠陥を形成し、さらに大きな応力を加えると線欠陥が集合して面欠陥を形成し、やがて破断する。
※この「応力」の解説は、「格子欠陥」の解説の一部です。
「応力」を含む「格子欠陥」の記事については、「格子欠陥」の概要を参照ください。
応力
「応力」の例文・使い方・用例・文例
- 迅速な対応力
- 現場での迅速な対応力
- ヨーロッパの区分は戦争をしている圏に、絶えず増大する遠応力を生む
- 引張応力
- 応力強度は、単位面積当たりの力の単位で表される
- 行動パターンに柔軟性がなく順応力のないこと
- 応力という物体に生じる抵抗力
- 構造物などの材料で,安全上許し得る限度の応力の値
- 物体が外力に対して破壊せずに耐えられる限界の応力
- (力学で)交番応力という,材料の強度測定のために働かせる応力
- 剪断加工という,剪断応力を利用した材料切断方法
- 熱応力という,構造物などの温度が場所によって異なるとき,材料の内部に生ずる抵抗力
- 速度の異なる流体の間で,速度を一様にしようとする応力が生じる性質
- 物体が破壊する限界の応力
- 引っ張り応力という,物体に生じる力
- 加えた荷重によって材料が破壊されず,十分安全に使用できるように決めた応力の限界値
- ファミコンで身に付けた心性が肥大し,現実生活に対する適応力が欠落するという心の症状
- 応力の変化
- 剪断応力という,ずれに抗して物質内に生じる応力
- 金属に応力を繰り返し負荷したとき,金属に損傷が累積して強度が低下し,ついには破断すること
応力と同じ種類の言葉
- >> 「応力」を含む用語の索引
- 応力のページへのリンク