中心極限定理

デジタル大辞泉

ちゅうしんきょくげん‐ていり【中心極限定理】

読み方：ちゅうしんきょくげんていり

母集団から無作為にn個の標本を抽出することで得られる標本平均の分布は、nが大きくなるにしたがって、正規分布に近づくという定理。すなわち、母集団の確率分布によらず、同じ平均と分散で表される正規分布で近似できることを示す。

統計学用語辞典

中心極限定理

　平均値 μ^*，分散 σ^2* をもつ，任意の分布に従う乱数列 x1，x2， … ，xnが あるとき，その平均値

の確率分布は，n が大きくなるとき，平均値 μ^*，分散 σ^2* / n である正規分布に収束する。
　すなわち，

は，n が大きいとき，平均値 0，分散 1 の標準正規分布に従うとみなしてよい。
　これを，中心極限定理 という。


　例えば，一様乱数は，平均 E ( x ) = 1 / 2，分散 V ( x ) = 1 / 12 であるから，12 個の一様乱数の合計から 6 を引くだけで 簡単に，標準正規分布に従う正規乱数が発生できる。

OR事典

中心極限定理

読み方：ちゅうしんきょくげんていり
【英】：central limit theorem

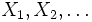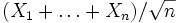互いに独立な確率変数列 において が 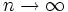のとき正規分布に近づくならば, 中心極限定理が成立するという. 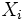が同一の分布をもち, 分散が有限ならば, 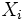の分布に関わらずに中心極限定理が成立することが知られている. この結果は, 正規分布の有用性を裏付けるものである.

「OR事典」の他の用語

確率と確率過程：	ランダムウォーク  一様分布  一様化  中心極限定理  信頼度  信頼性  停止時
待ち行列ネットワーク：	一般化ジャクソンネットワーク  一般化セミマルコフ過程  不感性  中心極限定理  仕事量保存型サービス  入力密度  内部推移

ウィキペディア

中心極限定理

出典: フリー百科事典『ウィキペディア（Wikipedia）』 (2024/12/06 14:44 UTC 版)

サイコロを n 回振ったときの出た目の和 S_n = X₁ + … + X_n の分布が n を大きくするに従って正規分布による近似に近づく様子

中心極限定理（ちゅうしんきょくげんていり、英: central limit theorem, CLT）は、確率論・統計学における極限定理の一つ。

大数の法則によると、ある母集団から無作為抽出した標本の算術平均は、標本の大きさを大きくすると母集団の母平均に近づく。これに対して中心極限定理は、標本の算術平均と母平均との誤差の確率分布が、定理の条件が満たされれば、標本の大きさを大きくすると近似的に期待値ゼロの「正規分布」になることをいう。

なお、母集団の分散が存在しないあるいは有限の実数にならないときには、標本平均と母平均の誤差の分布の極限が正規分布と異なる場合もある。

中心極限定理は、統計学における基本定理であり、例えば世論調査における必要サンプルのサイズの算出等に用いられる。

定理

以下の定理はLindeberg (1922) による。

期待値 μ と分散 σ² を持つ独立同分布 ("i.i.d.") に従う確率変数列 X₁, X₂, … に対し $\textstyle S_{n}:=\sum _{k=1}^{n}X_{k}$

ウィキメディア・コモンズには、中心極限定理に関連するカテゴリがあります。

• 確率論
• 大数の法則
• ド・モアブル=ラプラスの定理