マルコフ決定過程
【英】:Markov decision process
概要
状態遷移にマルコフ性をもつ確率システムの動的最適化のための数学モデル. 1960 年にハワードの著書が出版されたことで, 広く知られるようになり, その後, 理論・応用両面で様々な研究がなされている. 最適政策を求める計算アルゴリズムに関しても, 政策反復法, 値反復法(逐次近似法), 線形計画問題として定式化し単体法を用いる解法など, かなり大規模な問題にも耐え得るアルゴリズムが開発されている.
詳説
マルコフ決定過程 (Markov Decision Process: MDP) は, 待ち行列システムの制御, 在庫管理や, 信頼性システムの保全など, 確率システムの動的な最適化問題を定式化する能力に優れた数学モデルであり, 制御マルコフ過程 (controlled Markov process) とも呼ばれる. MDP は 1960 年にハワード (R. A. Howard) による名著 [3] が出版されたことにより, 広く知られるようになり, その後, 理論・応用・アルゴリズムの各面で膨大な数の多様な研究がなされてきている.
有限マルコフ決定過程 ここでは, 簡単のため, 離散時間の有限 MDP, すなわち状態数およびアクション数が有限のMDP を考える. 有限 MDP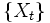 は以下の要素で構成される:
は以下の要素で構成される:
各状態でとるべきアクションを規定する規則, すなわち  から
から 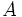 への写像
への写像  で
で 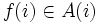 ,
, 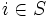 を満たすもの, を政策という. ここでは定常政策, すなわち写像
を満たすもの, を政策という. ここでは定常政策, すなわち写像  が時刻
が時刻  に依存しないもの, だけを考えるが, 下で述べる最適政策は非定常な政策を含む全ての政策の中で最適なものである. 定常政策の全体を
に依存しないもの, だけを考えるが, 下で述べる最適政策は非定常な政策を含む全ての政策の中で最適なものである. 定常政策の全体を 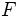 で表す.
で表す.
最適化すべき計画期間には, 有限計画期間と無限計画期間の2種類があるが, ここでは無限計画期間を考える. また, 政策の評価規範として最も多く採用され, よく研究されているのは, 下で定義される割引きコストと平均コストの 2 種類である. 以下で, 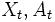 ,
, 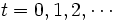 はそれぞれ時刻
はそれぞれ時刻  における状態とアクションを表す確率変数とし,
における状態とアクションを表す確率変数とし, ![\mathrm{E}_{i, f}[\cdot]\,](https://cdn.weblio.jp/e7/img/dict/orjtn/7dc53fb3ef703cbec1cdc183a132a0b6.png) は初期状態
は初期状態 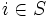 , 政策
, 政策 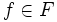 のもとでの期待値を表すものとする.
のもとでの期待値を表すものとする.
割引きコスト問題 割引き因子を 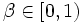 とする無限計画期間上の期待総割引きコスト (
とする無限計画期間上の期待総割引きコスト (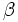 -割引きコスト) :
-割引きコスト) :
![u_{\beta,f}(i)
:= \mathrm{E}_{i, f} \left[ \sum_{t=0}^{\infty} \beta^{t}c(X_{t},A_{t}) \right],
\quad i \in S](https://cdn.weblio.jp/e7/img/dict/orjtn/f9be0b74fcd148872077e713d6da7829.png)
を, すべての初期状態 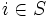 に対し, 最小化する政策
に対し, 最小化する政策 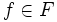 (
(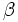 -割引き最適政策) を求めよ.
-割引き最適政策) を求めよ.
平均コスト問題 無限計画期間における長時間平均の単位時間当り期待コスト (平均コスト) :
![g_{f}(i)
:= \limsup_{T \to +\infty}
\frac{1}{T+1} \mathrm{E}_{i, f} \left[ \sum_{t=0}^{T} c(X_{t}, A_{t}) \right]](https://cdn.weblio.jp/e7/img/dict/orjtn/e1687770e3ecc41a283ddf2cf91b62e5.png)
以下では, 割引きコスト問題において, よく知られている結果を概説しよう. いま最適 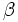 -割引きコスト関数を
-割引きコスト関数を
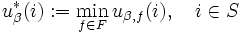
と定義すると, これは最適性方程式と呼ばれるつぎの関数方程式の一意的な解である:

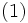
各状態 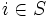 に対して, 最適性方程式 (1) の右辺の
に対して, 最適性方程式 (1) の右辺の 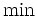 を達成する (任意の) アクションを
を達成する (任意の) アクションを 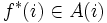 で表すと, それらで構成される政策
で表すと, それらで構成される政策 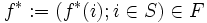 は
は 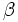 -割引き最適政策である.
-割引き最適政策である.
最適性方程式 (1) の標準的な数値解法としては, a. ハワードの提案による政策反復アルゴリズム (policy iteration method), b. 値反復アルゴリズム (逐次近似アルゴリズム), c. 線形計画による解法, などが挙げられる. 割引きコスト問題に対する政策反復アルゴリズムは以下の通りである.
ステップ 1 (政策評価) : 現在の政策 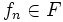 のもとでの
のもとでの 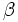 -割引きコスト関数
-割引きコスト関数 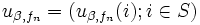 を, つぎの線形方程式系を解くことで計算する:
を, つぎの線形方程式系を解くことで計算する:
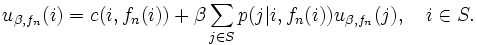
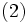
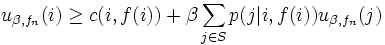
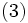
を, すべての状態 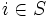 に対して成立させ, なおかつ, 少なくとも 1 つの状態では狭義の不等号で成立させる政策
に対して成立させ, なおかつ, 少なくとも 1 つの状態では狭義の不等号で成立させる政策 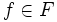 があれば,
があれば, 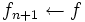 ,
, 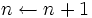 としてステップ 1 へ, さもなくば停止. 停止したとき, 最終の
としてステップ 1 へ, さもなくば停止. 停止したとき, 最終の 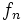 は
は 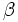 -割引き最適な政策である.
-割引き最適な政策である.
通常, ステップ 2 (政策改良) では, 各状態 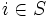 において式 (3) の右辺を最小化するアクションをとる政策が新しい政策
において式 (3) の右辺を最小化するアクションをとる政策が新しい政策 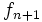 として選ばれる.
として選ばれる.
政策反復アルゴリズムは高速な解法として広く認められており, その収束に要する反復回数は, 経験的に, 問題の規模にあまり依存しない. この性質は非線形方程式系に対する数値解法であるニュートン・ラフソン法 (Newton-Raphson method) と共通のものであり, この政策反復アルゴリズムはニュートン・ラフソン法を適用することと等価であることが示されている. 政策反復アルゴリズムの弱点はステップ 1 (政策評価) において状態数だけの変数を持つ線形方程式系を解かなければならないことにある. したがって問題の規模が大きくなるにつれてその実行が負担となる. その弱点を克服するため, ステップ 1 を有限回の反復の逐次近似で代用する方法 (修正政策反復アルゴリズム) も提案されている.
ここでは離散時間の有限 MDP の割引きコスト問題のみを概説したが, a) 他の様々な評価規範, b) 状態空間/アクション空間の一般化, c) 状態遷移の時間間隔が確率的なセミマルコフ決定過程, についても多くの研究がなされている. 実際問題への適用の際に現れる情報の不完全性を明示的に考慮した, d) 不完全観測マルコフ決定過程, e) 遷移確率が未知パラメータを含む適応マルコフ決定過程, に関する研究も歴史が長い. また最近, 複数の評価規範を考慮し, f) すべての評価規範を目的関数として同時に最適化する多目的マルコフ決定過程, g) 一部の評価規範を制約条件に取り入れた制約付きマルコフ決定過程, なども関心を集め, 理論・応用・アルゴリズムの各面に関する活発な研究がなされている.
[1] D. P. Bertsekas, Dynamic Programming and Optimal Control, Vols. I, II, Athena Scientific, Belmont, Massachusetts, 1995.
[2] O. Hernández-Lerma and J. B. Lasserre, Discrete-Time Markov Control Processes, Basic Optimality Criteria, Springer-Verlag, New York, 1995.
[3] R. A. Howard, Dynamic Programming and Markov Processes, The MIT Press, Cambridge, Massachusetts, 1960.
[4] M. L. Puterman, Markov Decision Processes, John Wiley & Sons, New York, 1994.
[5] S. M. Ross, Introduction to Stochastic Dynamic Programming, Academic Press, New York, 1983.
[6] P. Whittle, Optimization over Times: Dynamic Programming and Stochastic Control, Vols. I, II, John Wiley & Sons, New York, 1983.
| 確率と確率過程: | マルコフ型到着過程 マルコフ変調ポアソン過程 マルコフ性 マルコフ決定過程 マルコフ連鎖 マルコフ連鎖の数値解法 マルコフ過程 |
マルコフ決定過程
(Markov Decision Process から転送)
出典: フリー百科事典『ウィキペディア(Wikipedia)』 (2025/06/18 18:47 UTC 版)
マルコフ決定過程(マルコフけっていかてい、英: Markov decision process; MDP)は、状態遷移が確率的に生じる動的システム(確率システム)の確率モデルであり、状態遷移がマルコフ性を満たすものをいう。 MDP は不確実性を伴う意思決定のモデリングにおける数学的枠組みとして、強化学習など動的計画法が適用される幅広い最適化問題の研究に活用されている。 MDP は少なくとも1950年代には知られていた[1]が、研究の中核は1960年に出版された Ronald A. Howard の "Dynamic Programming and Markov Processes" に起因する[2]。 MDP はロボット工学や自動制御、経済学、製造業を含む幅広い分野で用いられている。
概要

マルコフ決定過程は離散時間における確率制御過程 (stochastic control process) である。 各時刻において過程 (process) はある状態 (state) を取り、意思決定者 (decision maker) はその状態において利用可能な行動 (action) を任意に選択する。 その後過程はランダムに新しい状態へと遷移し、その際に意思決定者は状態遷移に対応した報酬 (reward) を受けとる。
遷移後の状態 ![]() カテゴリ
カテゴリ
- Markov Decision Processのページへのリンク
 :
:  : 状態
: 状態  でとり得る
でとり得る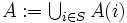 :
: 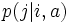 ,
, 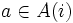 : 状態
: 状態 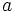 をとったとき, つぎの
をとったとき, つぎの に
に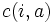 ,
, 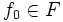 を
を
